
- •Введение
- •Глава 1. Элементы векторного анализа
- •1. Векторы и действия над ними
- •2. Математическое понятие поля. Градиент
- •3. Дивергенция. Теорема Остроградского-Гаусса
- •4. Ротор. Теорема Стокса
- •5. Некоторые соотношения векторного анализа
- •6. Операции в криволинейных координатах
- •В цилиндрических координатах
- •В сферических координатах
- •7. О дифференциальных уравнениях с частными производными
- •Глава 2. Уравнения лапласа и пуассона
- •8. Дельта-функция Дирака
- •9. Интегрирование уравнения Пуассона
- •10. Граничные задачи для уравнения Лапласа
- •11. Метод разделения переменных
- •Г лава 3. Гармонические колебания и волны
- •12. Гармонические колебания и метод комплексных амплитуд
- •13. Волновые процессы и их математическое описание
- •14. Вращение декартовой системы координат
- •Глава 4. Решения волновых уравнений
- •15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера
- •16. Уравнение Бесселя и цилиндрические функции
- •17. Решение однородного уравнения Гельмгольца методом разделения переменных
- •Глава 5. Краевые задачи электродинамики
- •18. Граничные задачи для уравнения Гельмгольца. Собственные функции и собственные значения
- •19. Ортогональные системы функций и ряды Фурье
- •20. Сведения из алгебры
- •21. Проекционные методы
- •Список литературы
- •Контрольные задания
Глава 4. Решения волновых уравнений
Ниже рассматривается ряд вопросов, связанных с математическим аппаратом, применяемым в гл. 4 книги [1]. До этого подробно обсуждались только свободные поля - волны без источников. Теория излучения и дифракции - это анализ полей вынужденных и, соответственно, условий возбуждения волн. Поэтому в дополнение к тому, что уже известно из п. 13 о решениях однородных уравнений - волнового уравнения (7.11) и уравнения Гельмгольца (7.6), теперь надо будет познакомиться с интегрированием уравнений неоднородных - уравнения Гельмгольца (7.10) и уравнения Даламбера (7.12). Собирательно будем называть все эти уравнения волновыми.
Другая тема данной главы - получение решений однородного уравнения Гельмгольца методом разделения переменных в декартовых, цилиндрических, а также сферических координатах. При подготовке этого материала сообщаются сведения о некоторых специальных функциях, главным образом, о функциях цилиндрических. Указанные функции используются в курсе электродинамики при изучении распространения электромагнитных волн в различных направляющих системах.
15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера
15.1. Функция Грина для уравнения Гельмгольца. Начнём с записи уравнения Даламбера в виде
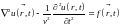 (15.1)
(15.1)
В простейшем и в то же время
весьма важном случае функция
 ,
которая выражает «вынуждающую силу»,
имеет характер гармонических колебаний:
,
которая выражает «вынуждающую силу»,
имеет характер гармонических колебаний:
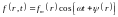 .
Вид гармонических колебаний имеет при
этом и решение:
.
Вид гармонических колебаний имеет при
этом и решение:
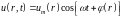 Используя метод комплексных амплитуд,
т. е. внося в (15.1)
Используя метод комплексных амплитуд,
т. е. внося в (15.1)
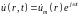 и
и
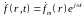 получаем неоднородное уравнение
Гельмгольца относительно
получаем неоднородное уравнение
Гельмгольца относительно
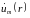 :
:
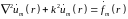 , (15.2)
, (15.2)
где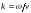 .
Подобная операция уже обсуждалась в п.
12.2. В электродинамике встречаются
уравнения Гельмгольца с комплексным
k;
подчеркивая это
введением символа
.
Подобная операция уже обсуждалась в п.
12.2. В электродинамике встречаются
уравнения Гельмгольца с комплексным
k;
подчеркивая это
введением символа
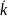 и ограничиваясь пока
скалярной формой, запишем:
и ограничиваясь пока
скалярной формой, запишем:
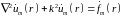 (15.2а)
(15.2а)
Решение неоднородного уравнения Гельмгольца будем искать тем же методом, который был применен в п. 9 к уравнению Пуассона (9.1). При этом понадобится функция Грина, т. е. в данном случае решение уравнения
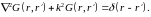 (15.3)
(15.3)
Интересующая нас функция Грина имеет вид:
 (15.4)
(15.4)
Прежде чем двигаться дальше,
проверим, что формула (15.4), действительно,
выражает решение уравнения (15.3). Для
этого достаточно убедиться, что
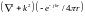 является
дельта-функцией, согласно её определению
(8.6), (8.7). Непосредственное дифференцирование
показывает, что
является
дельта-функцией, согласно её определению
(8.6), (8.7). Непосредственное дифференцирование
показывает, что
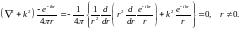 (15.5)
(15.5)
Далее, возьмём объем V, содержащий начало координат, и выделим сферу ΔV с центром в нём (т. е. при r = 0), имеющую радиус ρ. Ввиду (15.5)
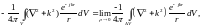
причём в силу теоремы Остроградского-Гаусса
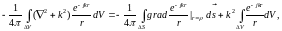
где ΔS - поверхность сферы ΔV (r = ρ на ΔS). При ρ → 0 второе слагаемое исчезает (ΔV = 0(ρ3)), а первое даёт:
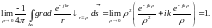
Таким образом,
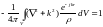 (15.6)
(15.6)
Исследуемая функция, как
видно, является дельта-функцией
δ(r),
а при замене r
→ |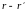 |
становится дельта-функцией
δ(
|
становится дельта-функцией
δ(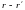 ).
Поэтому формула (15.4) подтверждена. Здесь
же отметим, что, как и в п. 9.1,
).
Поэтому формула (15.4) подтверждена. Здесь
же отметим, что, как и в п. 9.1,
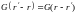 , (15.7)
, (15.7)
т. е. функция Грина симметрична относительно обоих аргументов.
15.2. Выражение решения неоднородного уравнения Гельмгольца.
Будем искать общий вид
решения неоднородного уравнения
Гельмгольца (15.2). С этой целью выполним
в (16.2) умножение на
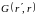 ,
а в (15.3) - на ит
,
а в (15.3) - на ит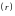 ;
произведём вычитание левых и правых
частей и интегрирование полученных
выражений как функций r
по V.
В результате получим:
;
произведём вычитание левых и правых
частей и интегрирование полученных
выражений как функций r
по V.
В результате получим:

Выполним, далее, следующие преобразования (ср. п 9.2):
а) объёмный интеграл слева заменим поверхностным при помощи теоремы Грина (5.14);
б) во втором слагаемом справа
произведем интегрирование по
формуле (8.7), что даёт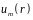 ;
;
в) произведём замену
обозначений
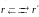 .
Ввиду (15.7) это не распространяется на
функцию Грина.
.
Ввиду (15.7) это не распространяется на
функцию Грина.
В итоге находим общий вид решения уравнения (15.2) в следующей форме:
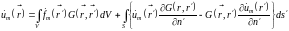 (15.8)
(15.8)
(обозначения здесь те же, что и в п. 9.2; заметим, что равенства (15.8) и (9.6) идентичны по форме).
Внося в (15.8) выражение функции Грина (15.4), получаем:
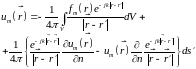 (15.9)
(15.9)
Собственно говоря, как видно
из (15.8) и (15.9), для нахождения решения
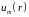 в
некоторой области V
надо располагать
сведениями о его поведении на внешней
границе S:
в поверхностный
интеграл входят функции
в
некоторой области V
надо располагать
сведениями о его поведении на внешней
границе S:
в поверхностный
интеграл входят функции
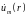 и
и
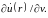
Для дальнейшего наиболее
интересен случай, когда решение уравнения
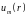 ищется
во всем безграничном пространстве, в
то время как вынуждающая сила
ищется
во всем безграничном пространстве, в
то время как вынуждающая сила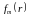 отлична от нуля только в некоторой
ограниченной области. Граница S
области V
при этом относится в
бесконечность. Пусть рассматриваемые
решения обладают таким свойством, что
поверхностный интеграл в (15.9) исчезает
(необходимые уточнения будут
сделаны в п. 4). Тогда решение
отлична от нуля только в некоторой
ограниченной области. Граница S
области V
при этом относится в
бесконечность. Пусть рассматриваемые
решения обладают таким свойством, что
поверхностный интеграл в (15.9) исчезает
(необходимые уточнения будут
сделаны в п. 4). Тогда решение
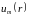 выражается следующей весьма важной
формулой:
выражается следующей весьма важной
формулой:
 . (15.10)
. (15.10)
Интегрирование здесь
фактически распространяется только на
область, в которой .
.
Разумеется, все полученные
результаты сохраняют формальный смысл
и при комплексном k;
заменив k
на
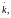 сразу же из (15.10)
получаем решение уравнения (15.2а). Наконец,
взяв векторное уравнение Гельмгольца
сразу же из (15.10)
получаем решение уравнения (15.2а). Наконец,
взяв векторное уравнение Гельмгольца
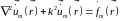 (15.11)
(15.11)
и рассматривая отдельно его проекции на оси декартовой системы координат (как это делалось в п.9.4 с векторным уравнением Пуассона), находим при помощи (15.10) его решение в виде:
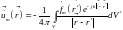 . (15.12)
. (15.12)
15.3. Выражение решения
уравнения Даламбера.
Перейдём к уравнению
Даламбера (16.1). При произвольной
зависимости от времени решение
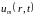 и
вынуждающую силу
и
вынуждающую силу
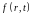 можно
представить в виде интегралов Фурье
(12.25):
можно
представить в виде интегралов Фурье
(12.25):
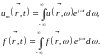 (15.13)
(15.13)
Умножим все члены уравнения
(15.1) на
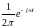 и
проинтегрируем по t
в пределах от -∞ до
∞. Ввиду (12.26),
и
проинтегрируем по t
в пределах от -∞ до
∞. Ввиду (12.26),
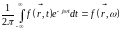 (15.14)
(15.14)
и
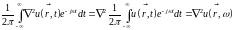 (15.15)
(15.15)
Что касается второго члена (15.1), содержащего дифференцирование по t, то соответствующий интеграл придется преобразовать путём двукратного интегрирования по частям:
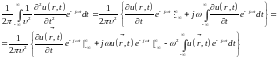
Полагая, что при t = ± ∞ решение и его производная по времени равны нулю и обозначая по-прежнему k = ω/υ, находим:
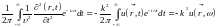 (15.16)
(15.16)
И, наконец, сопоставляя
(15.14) - (15.16), на основании (15.1)
получаем относительно спектральной
плотности
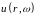 следующее неоднородное уравнение
Гельмгольца:
следующее неоднородное уравнение
Гельмгольца:
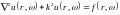 , (15.17)
, (15.17)
по форме совпадающее с (15.2).
Решение уравнения (15.17), таким образом, можно сразу же написать на основании формулы (15.10):
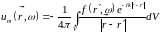 , (15.18)
, (15.18)
Чтобы построить решение уравнения Даламбера (15.1), составим первый из интегралов Фурье (15.13). Умножая левую и правую части (15.18) на еjωt и интегрируя по ω от -∞ до ∞, имеем:

Учитывая, что
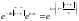
пишем:
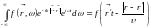
Действительно, это прямое
следствие второй формулы (15.13), где t
заменено на
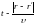 .
Итак, окончательно:
.
Итак, окончательно:
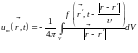 . (15.19)
. (15.19)
Решение уравнения Даламбера получено. Попробуем истолковать его и привлечём для этой цели решение (9.8) уравнения Пуассона (9.1); а также однородное волновое уравнение (7.11), различные решения которого рассматривались в п. 13. Там было показано, что υ имеет смысл фазовой скорости распространяющейся волны. Предположим, что υ ∞.
Мгновенное распространение фактически, означает исчезновение волнового процесса, и действительно, уравнение Даламбера (15.1) при этом переходит в уравнение Пуассона (9.1), а решение (15.19) - в (9.8).
Решение (15.19) выражает волновой процесс, возбуждаемый в пространстве источниками, расположенными в той области, где f 0. Действие источника в точке Р(r') не передаётся в точку наблюдения М(r) мгновенно, оно запаздывает на время необходимое для распространения волнового процесса; это и отражает полученное решение (15.19).
Результат (15.19) позволяет записать также решение векторного уравнения Даламбера:
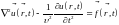 , (15.20)
, (15.20)
поскольку при проецировании на оси декартовой системы координат оно сводится к трём скалярным (ср. п. 9.4):
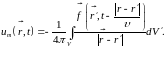 (15.21)
(15.21)
15.4. Расходящиеся и сходящиеся волны. Условие излучения. Вернёмся к полученным в п. 2 решениям уравнений Гельмгольца (15.10) и (15.12). Мы должны внимательно проследить условия, при которых эти решения были получены. Во-первых, рассмотрим поверхностный интеграл в (15.9), который должен уничтожаться.
Зафиксировав точку
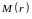 ,
в которой исследуется
решение
,
в которой исследуется
решение
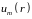 (15.9), будем относить границу S
объема V
в бесконечность,
представляя её себе как сферическую
поверхность радиуса r'
(рис. 9.1). При этом v'
= r',
и подынтегральное выражение поверхностного
интервала в (15.9) принимает вид:
(15.9), будем относить границу S
объема V
в бесконечность,
представляя её себе как сферическую
поверхность радиуса r'
(рис. 9.1). При этом v'
= r',
и подынтегральное выражение поверхностного
интервала в (15.9) принимает вид:
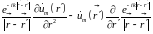
а поскольку при r'
∞ исчезает разница между
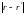 и
r',
то в пределе оно оказывается следующим:
и
r',
то в пределе оно оказывается следующим:
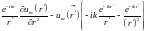 .
.
Учитывая, что S = 4π(r/)2, приходим к выводу, что поверхностный интеграл в (15.9) при отнесении границы в бесконечность исчезнет, если
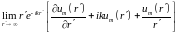 = 0.
= 0.
Отбрасывая несущественный общий множитель и член бесконечно малого порядка в скобках, а также изменяя обозначение аргумента (r' r), получаем следующее условие
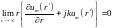 , (15.22)
, (15.22)
которому должны удовлетворять
решения
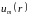 определяемые
по формуле (15.10). Это так называемое
условие излучения.
определяемые
по формуле (15.10). Это так называемое
условие излучения.
Легко убедиться, что условию излучения удовлетворяют лишь решения, имеющие при г ∞ вид расходящихся сферических волн:
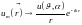 при r
∞ (15.23)
при r
∞ (15.23)
(п.13.3); сходящиеся же волны (с экспоненциальным множителем вида eikr ) автоматически отбрасываются.
Взяв, далее, уравнение
(15.2а) с комплексным
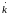 ,
без труда убедимся,
что условие излучения (15.22), в котором
теперь надо взять
= k'
- ik'',
будет удовлетворено,
если при r
∞ решение имеет
характер расходящейся затухающей волны
(в (15.23) берётся
,
для которого k'
> 0 и k">0).
,
без труда убедимся,
что условие излучения (15.22), в котором
теперь надо взять
= k'
- ik'',
будет удовлетворено,
если при r
∞ решение имеет
характер расходящейся затухающей волны
(в (15.23) берётся
,
для которого k'
> 0 и k">0).
Все рассмотрение немедленно
обобщается и на случай векторного
уравнения Гельмгольца (15.11) с его решением
(15.12); поскольку условие (15.22) налагается
на скалярные декартовы
компоненты функции
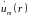 то
должно быть:
то
должно быть:
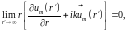 (15.24)
(15.24)
или
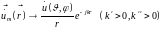 при
r→∞. (15.25)
при
r→∞. (15.25)
Перейдя, наконец, к скалярному и векторному уравнениям Даламбера (15.1) и (15.20), мы также должны заключить, что их решения вида (15.19) и (15.21) закономерны, поскольку в рассмотрение входят лишь расходящиеся волны.
Все перечисленные решения
(15.10), (15.12), (15.19) и (15.21) по своему характеру
действительно выражают расходящиеся
волны (см. рассуждение в конце п. 3):
волновой процесс, возбуждаемый в области
источника (где
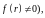 запаздывая,
распространяется в пространстве. Этот
характер уже определяется выбранной
функцией Грина (15.4). Надо иметь в виду,
что имеется также функция Грина
запаздывая,
распространяется в пространстве. Этот
характер уже определяется выбранной
функцией Грина (15.4). Надо иметь в виду,
что имеется также функция Грина
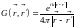 (15.26)
(15.26)
(проверка производится совершенно так же, как в п. 1), с которой мы бы получили вместо (15.10), (15.12), (15.19) и (15.21) аналогичные решения типа сходящихся волн. Последние, однако, поскольку рассматривается бесконечное пространство, физически бессодержательны. Действительно, решение
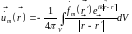 (15.27)
(15.27)
при r
∞ ведет себя как
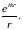
Для поглощающей среды, т. е. такой, в которой расходящаяся волна затухает (см. выше), должно быть k" > 0. Но при этом
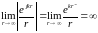 ,
,
что легко проверяется по правилу Лопиталя:
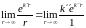 .
.
