
- •1.Кинематика точки. Система координат. Траектория движения точки. Способы задания уравнений движения тела.
- •5.Относительное движение. Абсолютная скорость и абсолютное ускорение.
- •10. Центр тяжести. Методы нахождения центров тяжести (симметричные тела, отрицательные объемы). Центры тяжести простейших фигур.
- •11.Введение в динамику. Второй закон ньютона.
- •12.Дифференциальные движения материальной точки (естественный и координатный способ).
- •13.Прямолинейное движение материальной точки.
- •14.Свободные колебания материальной точки.
- •15.Свободные колебания с учетом сопротивления.
- •18.Теорема об изменении количества движения материальной системы.
- •19.Теорема Эйлера.
- •20.Теорема о движении центра масс.
- •21.Теорема об изменении момента количества движения материальной системы.
- •22.Динамика вращательного движения вокруг неподвижной оси.
- •23.Работа и мощность.
- •24.Теорема об изменении кинетической энергии. Теорема Кенига.
- •25.Принцип Даламбера.
- •26.Принцип Лагранжа (принцип возможных перемещений).
- •28.Уравнение Лагранжа 2-го рода.
12.Дифференциальные движения материальной точки (естественный и координатный способ).
Основное
уравнение динамики
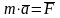 можно
записать так
можно
записать так
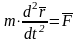 или так
или так
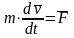 Проецируя
уравнение
на оси координат получаем
Проецируя
уравнение
на оси координат получаем
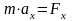
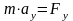
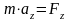
так
как 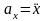 ,
, 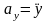 ,
, 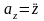 ,
то
,
то
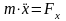
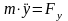
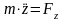
Частные
случаи: А) Точка движется в плоскости.
Выбираем в плоскости координаты xOy
получаем
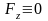 Б) Точка движется по прямой. Выбираем
на прямой координату Ox
получаем
Б) Точка движется по прямой. Выбираем
на прямой координату Ox
получаем
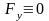 .
Основное уравнение динамики
можно спроецировать на естественные
подвижные оси.
.
Основное уравнение динамики
можно спроецировать на естественные
подвижные оси.
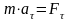 ,
, 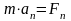 ,
, 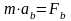
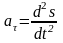 ,
,
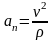 ,
,
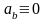
13.Прямолинейное движение материальной точки.
Дифференциальное
уравнение прямолинейного движения
точки вдоль оси Оx
имеет вид:
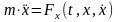 ,
Начальные условия
,
Начальные условия
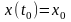 ,
, 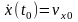 .
Наиболее важные случаи.1. Сила постоянна.
.
Наиболее важные случаи.1. Сила постоянна.
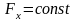 ,
,
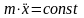 ,
,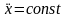 .
Имеем равнопеременное движение (движение
с постоянным ускорением) 2. Сила зависит
от времени.
.
Имеем равнопеременное движение (движение
с постоянным ускорением) 2. Сила зависит
от времени.
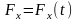 ,
,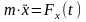 ,
,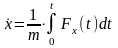 ,
,
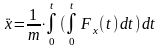 .
3. Сила зависит от координаты или
скорости. Силу, зависящую от координаты
х
.
3. Сила зависит от координаты или
скорости. Силу, зависящую от координаты
х
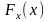 ,
создают упругие тела при их деформации
(например, сжатая или растянутая
пружина).
.
Сила, зависящая от скорости движения
,
создают упругие тела при их деформации
(например, сжатая или растянутая
пружина).
.
Сила, зависящая от скорости движения
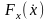 ,
это сила сопротивления (воздуха, воды
и т.д.)
,
это сила сопротивления (воздуха, воды
и т.д.)
14.Свободные колебания материальной точки.
15.Свободные колебания с учетом сопротивления.
16.Вынужденные колебания. Рассмотрим важный случай колебаний, возникающих, когда на точку, кроме восстанавливающей силы , действует еще периодически изменяющаяся со временем сила , проекция которой на ось Ох равна
![]() .
Эта сила называется возмущающей силой,
а колебания, происходящие при действии
такой силы, называются вынужденными.
Величина Р является частотой возмущающей
силы Возмущающей силой может быть сила,
изменяющаяся со временем и по другому
закону. Мы ограничимся рассмотрением
случая, когда определяется указанным
равенством. Такая возмущающая сила
называетсягармонической. Рассмотрим
движение точки, на которую, кроме
восстанавливающей силы , действует
только возмущающая сила . Дифференциальное
уравнение движения в этом случае
.
Эта сила называется возмущающей силой,
а колебания, происходящие при действии
такой силы, называются вынужденными.
Величина Р является частотой возмущающей
силы Возмущающей силой может быть сила,
изменяющаяся со временем и по другому
закону. Мы ограничимся рассмотрением
случая, когда определяется указанным
равенством. Такая возмущающая сила
называетсягармонической. Рассмотрим
движение точки, на которую, кроме
восстанавливающей силы , действует
только возмущающая сила . Дифференциальное
уравнение движения в этом случае![]() .
Разделим обе части этого уравнения на
т и положим
.
Разделим обе части этого уравнения на
т и положим
![]() .
Тогда, учитывая обозначение, приведем
уравнение движения к виду
.
Тогда, учитывая обозначение, приведем
уравнение движения к виду
![]() .
Уравнение является дифференциальным
уравнением вынужденных колебаний точки
при отсутствии сопротивления. Его
решением, как известно из теории
дифференциальных уравнений, будет ,
где -общее решение уравнения без правой
части, а - какое-нибудь частное решение
полного уравнения. Полагая, что p = k,
будем искать решение в виде
.
Уравнение является дифференциальным
уравнением вынужденных колебаний точки
при отсутствии сопротивления. Его
решением, как известно из теории
дифференциальных уравнений, будет ,
где -общее решение уравнения без правой
части, а - какое-нибудь частное решение
полного уравнения. Полагая, что p = k,
будем искать решение в виде
![]() где А - постоянная величина, которую
надо подобрать так, чтобы равенство
обратилось в тождество. Подставляя
значение и его второй производной в
уравнение будем иметь:
где А - постоянная величина, которую
надо подобрать так, чтобы равенство
обратилось в тождество. Подставляя
значение и его второй производной в
уравнение будем иметь:
![]() .
Это равенство будет выполняться при
любом t, если
.
Это равенство будет выполняться при
любом t, если
![]() или
или
![]() .
Таким образом, искомое частное решение
будет
.
Таким образом, искомое частное решение
будет
![]() .
Так как
.
Так как
![]() , а общее решение имеет окончательно
вид
, а общее решение имеет окончательно
вид
![]() ,
где а и - постоянные интегрирования,
определяемые по начальным данным.
Решение показывает, что колебания точки
складываются в этом случае из: 1) колебаний
с амплитудой а (зависящей от начальных
условий) и частотой k, называемых
собственными колебаниями, и 2) колебаний
с амплитудой А (не зависящей от начальных
условий) и частотой р, которые называются
вынужденными колебаниями. Частота р
вынужденных колебаний, как видно, равна
частоте возмущающей силы. Амплитуду
этих колебаний, если разделить числитель
и знаменатель на , можно представить в
виде:
,
где а и - постоянные интегрирования,
определяемые по начальным данным.
Решение показывает, что колебания точки
складываются в этом случае из: 1) колебаний
с амплитудой а (зависящей от начальных
условий) и частотой k, называемых
собственными колебаниями, и 2) колебаний
с амплитудой А (не зависящей от начальных
условий) и частотой р, которые называются
вынужденными колебаниями. Частота р
вынужденных колебаний, как видно, равна
частоте возмущающей силы. Амплитуду
этих колебаний, если разделить числитель
и знаменатель на , можно представить в
виде:
г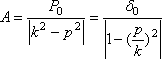 де
, т. е. есть величина статического
отклонения точки под действием силы .
Как видим, A зависит от отношения частоты
р возмущающей силы к частоте k собственных
колебаний. Подбирая различные соотношения
между р и k, можно получить вынужденные
колебания с разными амплитудами. При
амплитуда равна (или близка к этой
величине). Если величина р близка к k,
амплитуда A становится очень большой.
Когда , амплитуда A становится очень
малой (практически близка к нулю).Резонанс.
В случае, когда , т.е. когда частота
возмущающей силы равна частоте
собственных колебаний, имеет место так
называемое явление резонанса. Размахи
вынужденных колебаний при резонансе
будут со временем неограниченно
возрастать .
де
, т. е. есть величина статического
отклонения точки под действием силы .
Как видим, A зависит от отношения частоты
р возмущающей силы к частоте k собственных
колебаний. Подбирая различные соотношения
между р и k, можно получить вынужденные
колебания с разными амплитудами. При
амплитуда равна (или близка к этой
величине). Если величина р близка к k,
амплитуда A становится очень большой.
Когда , амплитуда A становится очень
малой (практически близка к нулю).Резонанс.
В случае, когда , т.е. когда частота
возмущающей силы равна частоте
собственных колебаний, имеет место так
называемое явление резонанса. Размахи
вынужденных колебаний при резонансе
будут со временем неограниченно
возрастать .
17.Система
материальных точек. Внешние и внутренние
силы. Д.У. системы дифференциальных
точек. Механической
системой материальных точек или тел
называется такая их совокупность, в
которой положение или движение каждой
точки (или тела) зависит от положения
и движения всех остальных. Материальное
тело мы также будем рассматривать как
систему материальных частиц (точек),
образующих это тело. Совокупность тел,
между которыми нет никаких сил
взаимодействия (например, группа летящих
в воздухе самолетов), механическую
систему не образует. В соответствии со
сказанным, силы, действующие на точки
или тела системы, можно разделить на
внешние и внутренние. Внешними называются
силы, действующие на точки системы со
стороны точек или тел, не входящих в
состав данной системы. Внутренними
называются силы, действующие на точки
системы со стороны других точек или
тел этой же системы. Будем обозначать
внешние силы символом -
![]() , а внутренние -
, а внутренние -
![]() .
Как внешние, так и внутренние силы могут
быть в свою очередь или активными, или
реакциями связей. Разделение сил на
внешние и внутренние является условным
и зависит от того, движение какой системы
тел мы рассматриваем. Внутренние силы
обладают следующими свойствами:1.
Геометрическая сумма (главный вектор)
всех внутренних сил системы равняется
нулю. В самом деле, по третьему закону
динамики любые две точки системы
действуют друг на друга с равными по
модулю и противоположно направленными
силами и , сумма которых равна нулю. 2.
Сумма моментов (главный момент) всех
внутренних сил системы относительно
любого центра или оси равняется нулю.
.
Как внешние, так и внутренние силы могут
быть в свою очередь или активными, или
реакциями связей. Разделение сил на
внешние и внутренние является условным
и зависит от того, движение какой системы
тел мы рассматриваем. Внутренние силы
обладают следующими свойствами:1.
Геометрическая сумма (главный вектор)
всех внутренних сил системы равняется
нулю. В самом деле, по третьему закону
динамики любые две точки системы
действуют друг на друга с равными по
модулю и противоположно направленными
силами и , сумма которых равна нулю. 2.
Сумма моментов (главный момент) всех
внутренних сил системы относительно
любого центра или оси равняется нулю.
Эти
уравнения, из которых можно определить
закон движения каждой точки системы,
называются дифференциальными уравнениями
движения системы в векторной форме.
Уравнения являются дифференциальными,
так как
![]() ;
входящие в правые части уравнений силы
будут в общем случае зависеть от времени,
координат точек системы и их скоростей.
;
входящие в правые части уравнений силы
будут в общем случае зависеть от времени,
координат точек системы и их скоростей.
