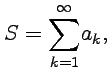- •Классификация функций по свойствам.
- •Основные элементарные функции. Понятия сложной и обратной функций. Элементарные функции и их классификация.
- •Бесконечно малые и бесконечно большие функции, свойства. Связь бесконечно больших и бесконечно малых функций.
- •Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
- •Основные свойства пределов функции. Замечательные пределы.
- •Непрерывность функции в точке. Свойства функций, непрерывных в точке. Непрерывность основных элементарных функций.
- •Односторонняя непрерывность. Точки разрыва функции и их классификация.
- •Определение и свойства функции, непрерывной на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения. Теорема об обратной функции.
- •Понятие производной функции в точке. Геометрический и механический смысл производной.
- •Правила вычисления производной, связанные с арифметическими действиями над функциями. Производные основных элементарных функций.
- •Производная сложной и обратной функций.
- •Производные функций, заданных в параметрическом виде и неявно.
- •Частные производные и дифференциалы высших порядков функции нескольких переменных.
- •Формальное определение
- •Понятия числового ряда, его суммы. Сходящиеся и расходящиеся числовые ряды. Необходимое условие сходимости числового ряда. Действия с числовыми рядами.
- •Знакопеременные числовые ряды. Понятия абсолютной и условной сходимости, их свойства.
- •Знакочередующиеся числовые ряды. Теорема Лейбница.
- •Числовые ряды с комплексными членами.
- •Функциональные ряды. Область сходимости функционального ряда. Равномерная сходимость функционального ряда. Признак Вейерштрасса.
- •Функциональный ряд
- •Сходимость
- •Свойства равномерно сходящихся функциональных рядов.
- •Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда, свойства степенных рядов.
- •Признаки сходимости
- •Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Формула Тейлора. Разложение основных элементарных функций в ряд Маклорена.
- •Формула Тейлора
- •Понятие тригонометрического ряда Фурье, условия его сходимости.
- •Основные элементарные функции комплексных переменных.
- •1. Дробно-рациональная функция
- •2. Показательная функция:
- •3. Тригонометрические функции:
- •4. Гиперболические функции:
- •5. Логарифмическая функция.
- •6. Общая степенная функция:
- •Дифференцируемость, условия Коши-Римана дифференцируемости функции комплексной переменной.
- •Определение аналитической функции комплексной переменной, свойства.
- •Интегрирование функций комплексной переменной. Дифференцирование Определение
- •Разложение аналитических функций в степенные ряды. Понятие ряда Лорана.
Знакопеременные числовые ряды. Понятия абсолютной и условной сходимости, их свойства.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
![]()
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
-
Пусть для знакочередующегося ряда
выполняются следующие условия:
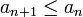 (монотонное
невозрастание {an})
(монотонное
невозрастание {an})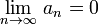 .
.
Тогда этот ряд сходится.
Если, выполнены все условия, и ряд из модулей ( ) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность существенна.
Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
![]() .
Ряд из модулей имеет вид
.
Ряд из модулей имеет вид ![]() —
это гармонический
ряд, который расходится.
—
это гармонический
ряд, который расходится.
Теперь воспользуемся признаком Лейбница:
знакочередование выполнено
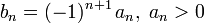
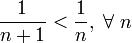
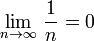 .
.
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
Знакочередующиеся числовые ряды. Теорема Лейбница.
Теорема Лейбница (признак Лейбница) — теорема об условной сходимости знакочередующихся рядов, сформулированная немецким математиком Лейбницем.
Формулировка
Теорема формулируется следующим образом. Знакочередующийся ряд
![]()
сходится, если выполняются оба условия:
Из теоремы Лейбница вытекает следствие, позволяющее оценить погрешность вычисления неполной суммы ряда:
![]()
Остаток
сходящегося знакочередующегося
ряда ![]() будет
по модулю меньше первого отброшенного
слагаемого:
будет
по модулю меньше первого отброшенного
слагаемого:
![]()
Числовые ряды с комплексными членами.
Числовым рядом комплексных чисел называется ряд вида:
|
(55) |
где ![]() -
последовательность комплексных чисел.
Необходимым и достаточным условием
сходимости ряда (55)
является критерий Коши, согласно
которому ряд
(55)
сходится тогда и только тогда, если
для
-
последовательность комплексных чисел.
Необходимым и достаточным условием
сходимости ряда (55)
является критерий Коши, согласно
которому ряд
(55)
сходится тогда и только тогда, если
для ![]() можно
указать такой номер
можно
указать такой номер ![]() ,
что
,
что 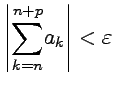 при
при ![]() и
любом натуральном
и
любом натуральном ![]() .
.
Ряд
(55)
называется абсолютно сходящимся,
если сходится ряд модулей 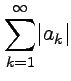 .
.
Решение задач, связанных с исследованием сходимости числовых рядов, основано на использовании признаков:
Д'Аламбера : ряд сходится, если начиная с некоторого , отношение
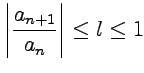 ,
, 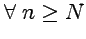 ;
;Коши : ряд сходится, если
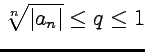 ,
;
,
;
а
также необходимого
условия сходимости : ![]() .
.
Функциональные ряды. Область сходимости функционального ряда. Равномерная сходимость функционального ряда. Признак Вейерштрасса.
Функциональный
ряд —
ряд, каждым членом которого, в отличие
от числового
ряда,
является не число, а функция ![]()
Функциональный ряд
![]()
![]() —
n-ная
частичная сумма.
—
n-ная
частичная сумма.
Сходимость
Ряд
называется сходящимся поточечно, если
последовательность ![]() его
частичных сумм сходится поточечно.
его
частичных сумм сходится поточечно.
Ряд называется сходящимся равномерно, если последовательность его частичных сумм сходится равномерно.
Признак Вейерштрасса.
Рассмотрим ряд:
![]()
Пусть
существует последовательность
такая,
что для любого ![]() выполняется
неравенство
выполняется
неравенство
![]()
Пусть, кроме того, ряд
сходится. Тогда ряд
сходится на множестве Х абсолютно и равномерно.
Для доказательства достаточно проверить справедливость критерия Коши.