- •Классификация функций по свойствам.
- •Основные элементарные функции. Понятия сложной и обратной функций. Элементарные функции и их классификация.
- •Бесконечно малые и бесконечно большие функции, свойства. Связь бесконечно больших и бесконечно малых функций.
- •Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
- •Основные свойства пределов функции. Замечательные пределы.
- •Непрерывность функции в точке. Свойства функций, непрерывных в точке. Непрерывность основных элементарных функций.
- •Односторонняя непрерывность. Точки разрыва функции и их классификация.
- •Определение и свойства функции, непрерывной на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения. Теорема об обратной функции.
- •Понятие производной функции в точке. Геометрический и механический смысл производной.
- •Правила вычисления производной, связанные с арифметическими действиями над функциями. Производные основных элементарных функций.
- •Производная сложной и обратной функций.
- •Производные функций, заданных в параметрическом виде и неявно.
- •Частные производные и дифференциалы высших порядков функции нескольких переменных.
- •Формальное определение
- •Понятия числового ряда, его суммы. Сходящиеся и расходящиеся числовые ряды. Необходимое условие сходимости числового ряда. Действия с числовыми рядами.
- •Знакопеременные числовые ряды. Понятия абсолютной и условной сходимости, их свойства.
- •Знакочередующиеся числовые ряды. Теорема Лейбница.
- •Числовые ряды с комплексными членами.
- •Функциональные ряды. Область сходимости функционального ряда. Равномерная сходимость функционального ряда. Признак Вейерштрасса.
- •Функциональный ряд
- •Сходимость
- •Свойства равномерно сходящихся функциональных рядов.
- •Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда, свойства степенных рядов.
- •Признаки сходимости
- •Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Формула Тейлора. Разложение основных элементарных функций в ряд Маклорена.
- •Формула Тейлора
- •Понятие тригонометрического ряда Фурье, условия его сходимости.
- •Основные элементарные функции комплексных переменных.
- •1. Дробно-рациональная функция
- •2. Показательная функция:
- •3. Тригонометрические функции:
- •4. Гиперболические функции:
- •5. Логарифмическая функция.
- •6. Общая степенная функция:
- •Дифференцируемость, условия Коши-Римана дифференцируемости функции комплексной переменной.
- •Определение аналитической функции комплексной переменной, свойства.
- •Интегрирование функций комплексной переменной. Дифференцирование Определение
- •Разложение аналитических функций в степенные ряды. Понятие ряда Лорана.
Производная сложной и обратной функций.
Производная обратной функции.
Пусть
функция ![]() дифференцируема
и строго монотонна на
дифференцируема
и строго монотонна на ![]() .
Пусть также в точке
.
Пусть также в точке ![]() производная
производная ![]() .
Тогда в точке
.
Тогда в точке ![]() определена дифференцируемая функция
определена дифференцируемая функция ![]() ,
которую называют обратной к
,
которую называют обратной к ![]() ,
а ее производная вычисляется по формуле
,
а ее производная вычисляется по формуле ![]() .
.
![]()
Пример:
Производная сложной функции.
Пусть
задана сложная
функция ![]() ,
т.е. переменная
,
т.е. переменная ![]() есть
функция переменной
есть
функция переменной ![]()
![]() ,
а переменная
есть,
в свою очередь, функция от независимой
переменной
,
а переменная
есть,
в свою очередь, функция от независимой
переменной ![]() .
.
Если ![]() и
и ![]() - дифференцируемые функции
своих аргументов, то сложная
функция
является
дифференцируемой функцией и ее производная
равна произведению производной данной
функции по промежуточному аргументу и
производной промежуточного аргумента по
независимой переменной:
- дифференцируемые функции
своих аргументов, то сложная
функция
является
дифференцируемой функцией и ее производная
равна произведению производной данной
функции по промежуточному аргументу и
производной промежуточного аргумента по
независимой переменной:
![]() .
.
Производные функций, заданных в параметрическом виде и неявно.
Пусть
задана зависимость двух переменных ![]() и
и ![]() от
параметра
от
параметра ![]() ,
изменяющегося в пределах от
,
изменяющегося в пределах от ![]() до
до ![]() :
:
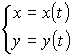
![]()
Пусть
функция ![]() имеет
обратную:
имеет
обратную: ![]() .
Тогда мы можем, взяв композицию
функций
.
Тогда мы можем, взяв композицию
функций ![]() и
и ![]() ,
получить зависимость
от
:
,
получить зависимость
от
: ![]() .
Зависимость величины
от
величины
,
заданная через зависимость каждой из
них от параметра
в
виде
.
Зависимость величины
от
величины
,
заданная через зависимость каждой из
них от параметра
в
виде ![]() ,
называется функцией
,
называется функцией ![]() ,
заданной параметрически.
,
заданной параметрически.
Производную
функции ![]() ,
заданной параметрически, можно выразить
через производные функций
,
заданной параметрически, можно выразить
через производные функций ![]() и
и ![]() :
поскольку
и,
по формуле производной обратной
функции,
:
поскольку
и,
по формуле производной обратной
функции, ![]() ,
то
,
то
![]()
где -- значение параметра, при котором получается интересующее нас при вычислении производной значение .
Заметим,
что применение формулы приводит нас к
зависимости между ![]() и
,
снова выраженной в виде параметрической
зависимости:
и
,
снова выраженной в виде параметрической
зависимости: ![]() ,
, ![]() ;
второе из этих соотношений -- то же,
что участвовало в параметрическом
задании функции
.
Несмотря на то, что производная не
выражена через
в
явном виде, это не мешает решать нам
задачи, связанные с нахождением
производной, найдя соответствующее
значение параметра
.
Покажем это на следующем примере.
;
второе из этих соотношений -- то же,
что участвовало в параметрическом
задании функции
.
Несмотря на то, что производная не
выражена через
в
явном виде, это не мешает решать нам
задачи, связанные с нахождением
производной, найдя соответствующее
значение параметра
.
Покажем это на следующем примере.
Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
Пример : Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2· у'-3(1· у+х· у')=0
следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х).
Б ИЛЕТ
15.
Первый
замечательный предел.
ИЛЕТ
15.
Первый
замечательный предел.
![]()
Для
доказательства возьмем вектор
![]() окружности радиуса 1 с центральным
углом, равным
окружности радиуса 1 с центральным
углом, равным
![]() (радиан),
(радиан),
![]() и проведем
и проведем
![]() .
Тогда пл.
.
Тогда пл.
![]() <
пл. сект.
<
пл.
<
пл. сект.
<
пл.
![]() или
или
![]() .
Разделив все части этого неравенства
на
.
Разделив все части этого неравенства
на
![]() >
0, получим
>
0, получим
![]() или
или
![]() .
Это неравенство, доказанное для любых
из интервала (0;
.
Это неравенство, доказанное для любых
из интервала (0;![]() ),
верно для любого
),
верно для любого
![]() из
интервала (-
;
)
в силу четности функций, входящих в это
неравенство.
из
интервала (-
;
)
в силу четности функций, входящих в это
неравенство.
Докажем,
что
![]()
(![]() )
при
)
при
![]()
А
раз
и
![]() ,
то
.
,
то
.
Кроме
того:
![]() =
=![]() 1
1
БИЛЕТ 16. Второй замечательный предел.
![]()
![]() .
.
На
первый взгляд кажется, что
при
имеет пределом единицу (так как 1+
при
имеет пределом единицу, а единица в
любой степени есть единица). Но в степень
![]() возводится
1+
,
а не единица. И вот из-за этой бесконечно
малой добавки
предел не равен единице. Чтобы
приблизительно представить себе
поведение функции
при
малых
приведем таблицу значений этой функции:
возводится
1+
,
а не единица. И вот из-за этой бесконечно
малой добавки
предел не равен единице. Чтобы
приблизительно представить себе
поведение функции
при
малых
приведем таблицу значений этой функции:
|
1/2 |
1/3 |
1/4 |
0.01 |
0.001 |
|
2.25 |
2.37… |
2.44… |
2.7047… |
2.7169… |
Из этой таблицы видно, что с уменьшением функция увеличивается. Оказывается, что это имеет место для всех >0, а из этого следует, что функция имеет предел.
Доказательство: Рассмотрим этот предел, как предел функции натурального аргумента на бесконечность. Тогда:
По определению Гейне:
![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]() Вычислим
Вычислим
![]() .
Рассмотрим
=
.
Рассмотрим
=![]() =
=![]()
![]() .
.
По
определению Гейне рассмотрим
![]() .
.
![]()
![]()
![]()
![]()

![]()
![]()
![]() *
*![]()
То
есть
=
=![]() =
.
=
.
Т акже
=
акже
=![]() =
=
![]() =
=
![]() =
=
![]()
1
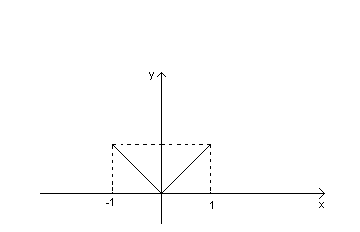
БИЛЕТ 17. Сравнение бесконечно малых функций. Примеры.
Определение:
![]() бесконечно
малая функция при
бесконечно
малая функция при
![]() ,
если
,
если
![]()
![]() .
Определение:
Пусть
.
Определение:
Пусть
![]() и
и![]() -
бесконечно малые функции при
.
Тогда:
-
бесконечно малые функции при
.
Тогда:
1)
и
эквивалентны при
(
~
,
),
если
![]() .
.
2)
,
-
бесконечно малые одного порядка малости
при
,
если
![]() .
3)
-
бесконечно малая более высокого порядка
малость, чем
.
.
3)
-
бесконечно малая более высокого порядка
малость, чем
.
(
=![]() (
),
),
если
(
),
),
если
![]() .
.
4).
имеет
![]() -й
порядок малости относительно
при
,
если
-й
порядок малости относительно
при
,
если
![]() .
.
5).
называется ограниченной относительно
бесконечно малой функции
при
,
если
![]()
![]()
![]() .
.
Примеры:
1).
![]() при
.
при
.
2).
![]() (
(![]() ,
-бесконечные
малости одного порядка).
,
-бесконечные
малости одного порядка).
3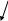 ).
).
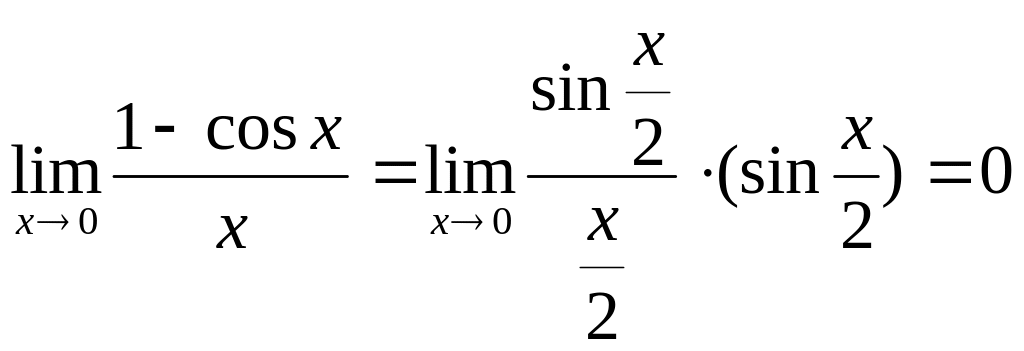 (
(![]()
![]() )
)
1 0
4). …
![]() (
(![]() )-
2-й порядок малости относительно
при
.
)-
2-й порядок малости относительно
при
.
5).
![]()
![]() -
произвольная.
-
произвольная.
БИЛЕТ 18. Эквивалентные бесконечно малые функции. Критерий эквивалентности. Теорема о замене на эквивалентные.
Определение:
функция
называется
бесконечно
малой
при
,
если
![]() =0.
=0.
Теорема (критерий эквивалентности):
Пусть , -бесконечно малые функции при .
![]() -
.
Тогда
~
при
-
.
Тогда
~
при
![]()
![]() .
.
Доказательства:
( ). Пусть ~ , , то есть .
![]()
![]()
![]() =0,
=0,
то есть .
(![]() ).
.,
.
).
.,
.
![]()
![]() =1.
=1.
Теорема (о замене на эквивалентные):
Пусть
функция
~![]() ,
~
,
~![]() при
и существует
при
и существует
![]() ,
тогда существует и
,
тогда существует и
![]() =
.
То есть выражение или функцию можно
заменять на эквивалентное.
=
.
То есть выражение или функцию можно
заменять на эквивалентное.
=
*![]() *
*![]() =
.
=
.

1 1
БИЛЕТ 19. Определения непрерывности функции в точке. Простейшие свойства непрерывных функций.
Определение
1:
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если
,
если
![]() .
.
Определение
2:
Функция
непрерывна
в точке
,
если
![]()
![]() ,
,
![]() .
.
Определение
3:
Функция
непрерывна
в точке
,
если
![]()
![]()
![]()
![]()
![]() .
.
Свойства непрерывных функций:
Теорема
1 (локальная огр.): Пусть
функция
непрерывна
в точке
,
тогда
![]()
![]()
![]() .
.
Теорема
2 (отделимость от 0): Пусть
функция
непрерывна
в точке
и
![]() ,
тогда
,
тогда
.
![]() .
.
Теорема
3 (арифметика непрерывных функций):
Пусть
,
![]() непрерывны
в точке
,
тогда:
непрерывны
в точке
,
тогда:
1).
![]() непрерывна в точке
.
непрерывна в точке
.
2).
![]() непрерывно в точке
.
непрерывно в точке
.
3).
Если
![]() ,
то
,
то
![]() непрерывно
в точке
.
непрерывно
в точке
.
БИЛЕТ 20. Непрерывность сложной функции.
Теорема:
если функция
![]() непрерывна
в точке
,
а функция
непрерывна
в точке
,
а функция
![]() непрерывна
в точке
непрерывна
в точке
![]() то сложная функция
то сложная функция
![]() непрерывна в точке
.
непрерывна в точке
.
Доказательство:
Возьмем
число
![]() >0.
Так как функция
>0.
Так как функция
![]() непрерывна
в точке
то
можно подобрать такое число
непрерывна
в точке
то
можно подобрать такое число
![]() ,
что
,
что
![]() для
любого
для
любого
![]() ,
такого, что
,
такого, что
![]() .
(1)
.
(1)
А
так как функция
непрерывна в точке
,
то для положительного числа![]() можно подобрать такое число
можно подобрать такое число
![]() ,
что
,
что
![]() для
любого
,
такого, что
.
(2)
для
любого
,
такого, что
.
(2)
Возьмем
любое число
такое, что
.
Тогда в силу (2)
число
удовлетворяет неравенству
,
и поэтому в силу (1)
![]() .
Так как все эти вычисления проведены
для любого
>0,
то непрерывность функции
в точке
доказана.
.
Так как все эти вычисления проведены
для любого
>0,
то непрерывность функции
в точке
доказана.
БИЛЕТ 21. Классификация разрывов. Примеры.
Определение: -точка разрыва функции , если в точке функция не является непрерывной.
Определение:
точка
-точка
устранимого разрыва функции
,
если существует
![]() ,
но
не
определена в точке
,
либо
,
но
не
определена в точке
,
либо
![]() .
.
Замечание: Если в точке устранимого разрыва доопределить (переопределить) функцию:
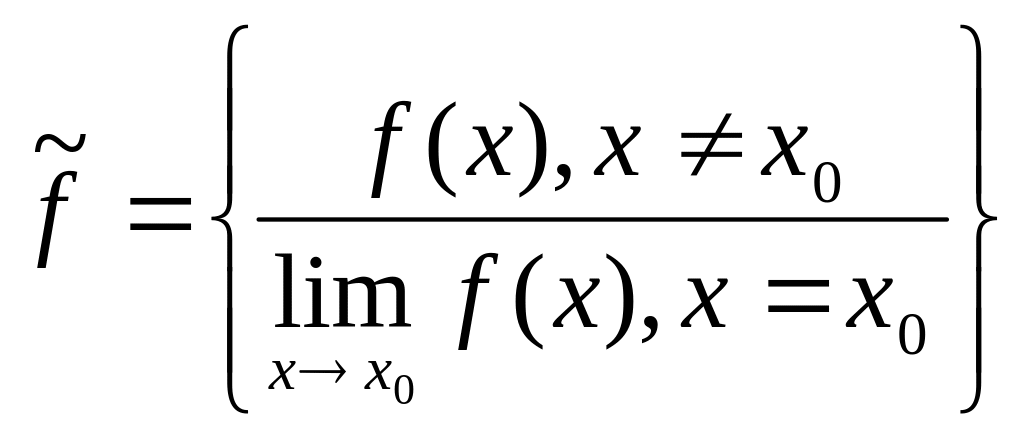
 -
непрерывна в точке
.
-
непрерывна в точке
.
Пример:
![]() .
.
![]() ,
,
![]() -
точка устранимого разрыва
.
-
точка устранимого разрыва
.
Если
![]() не
существует, то
-точка
неустранимого
не
существует, то
-точка
неустранимого
разрыва .
Определение: Пусть точка -точка неустранимого разрыва функции , тогда:
если существует
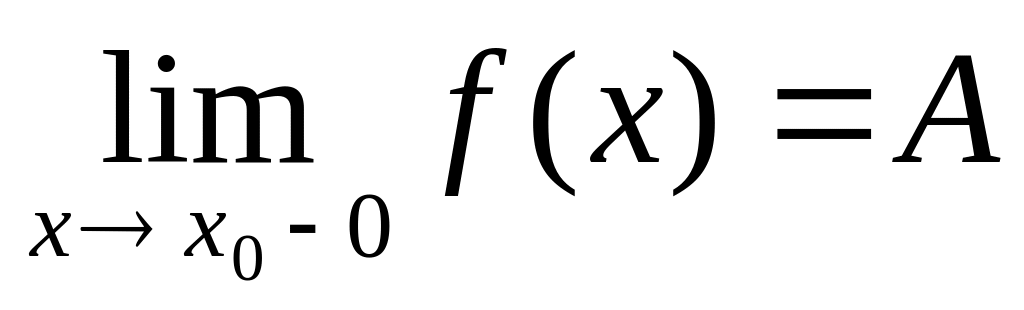 ,
то
,
то
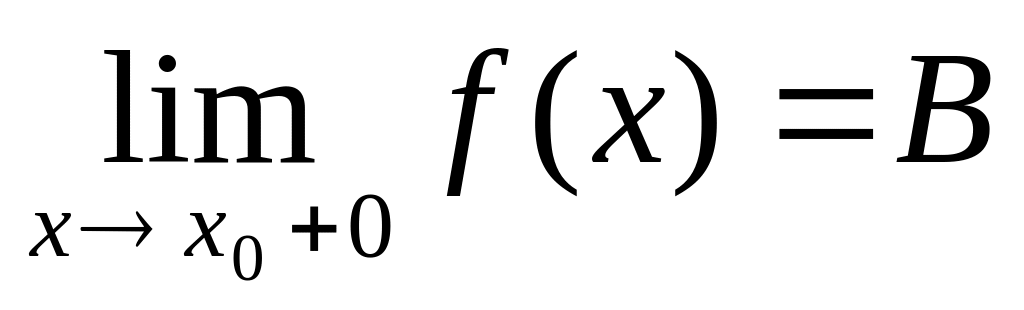 .
.если
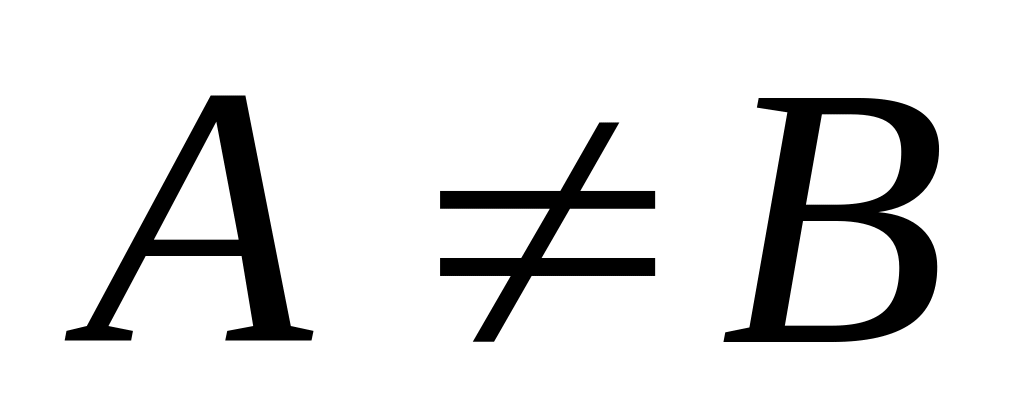 ,
то
-точка
разрыва функции
1-го рода.
,
то
-точка
разрыва функции
1-го рода.если
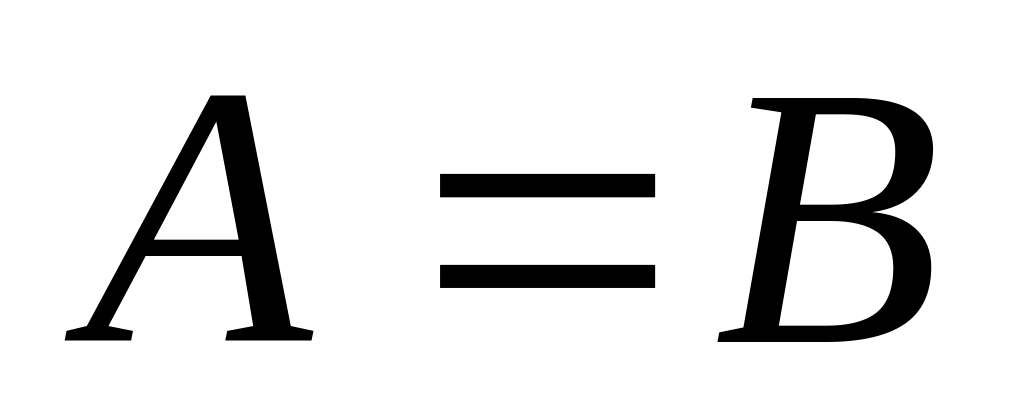 ,
то
-точка
разрыва функции
2-го рода.
,
то
-точка
разрыва функции
2-го рода.
П римеры:
римеры:
1).
![]() .
.
![]() ,
,
![]()
- точка разрыва 1-го рода.
2 ).
).
![]() .
.
![]() ,
,
![]()
- точка разрыва 2-го рода.
3 ).
).
![]()
,
![]()
- точка разрыва 2-го рода.
4 ).
).
![]()
![]()
![]()
![]()
![]() не
существует
точка
-
точка разрыва
2-го
рода.
не
существует
точка
-
точка разрыва
2-го
рода.
, . Точка - точка разрыва 2-го рода.
БИЛЕТ 22. Теорема о нуле непрерывной функции. Теорема Коши о промежуточном значении.
Определение:
непрерывна на
![]()
![]() ,
если
непрерывна в точке
,
,
если
непрерывна в точке
,
![]()
непрерывна
на
![]()
![]() ,
если
непрерывна в точке
,
и
,
если
непрерывна в точке
,
и
Существует
![]() ,
,
![]() .
.
Теорема:
Пусть
определена на
и
![]() ,
причем
,
причем
![]() .
Тогда
.
Тогда
![]() .
.
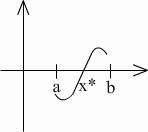
Пусть
![]() ,
,
![]() .
Используем метод деления отрезка
пополам.
.
Используем метод деления отрезка
пополам.
Обозначим:
![]() ,
,
![]() .
.
Определим
![]()
1)
=0![]() .
.
2)
<
0![]() ,
,
![]() .
.
3)
>
0![]() ,
,
![]() и так далее.
и так далее.
![]()
![]() .
.
![]()
![]()
![]() .
.
По
лемме о вложенных отрезках:
![]() ,
то есть
,
то есть
![]() .
.
![]() непрерывна
в точке
непрерывна
в точке
![]()
![]() .
.
![]()


 .
.
0
(![]() )
)
![]()
![]()
 .
.
![]() .
.
![]()
0 ( )
![]()
Следствие (т. о промежуточном значении непрерывной функции):
Пусть
![]() определена на
и
,
определена на
и
,
![]() ,
,
![]() ,
,
Тогда
![]() :
:
![]() .
.
Пусть
для ограничения
![]() .
.
Рассмотрим
произвольн.
:
![]()
![]() непрерывна
на
непрерывна
на
![]() .
.
![]()
![]()
Из этих двух утверждений следует:
![]() ,
то есть
,
то есть
![]() .
.
БИЛЕТ 23. Первая теорема Вейерштрасса.
Пусть
.
Тогда
ограничена
на![]() .
.
Доказательство:
Докажем,
что
![]()
![]() .
.
Предположим
противное, то есть
![]()
![]()
![]() .
Возьмем
.
Возьмем
![]() =1,2,3…
=1,2,3…
Получим
![]() :
:
1)
![]()
![]()
2)
![]()
Из
этих определений получаем
![]()
![]() .
.
=>
![]() -подпоследовательность
последовательности
:
-подпоследовательность
последовательности
:
![]() .
.
![]() -непрерывна
в точке
-непрерывна
в точке
![]() =>
=>
![]() .
.
-подпоследовательность
последовательности
:
![]() =>
=>
![]() .
Противоречие.
.
Противоречие.
Замечание:
Замкнутость
![]() по
существу.
по
существу.
![]() ,
,
![]() ,
но
,
но
Не
является ограниченной на
![]() .
.
БИЛЕТ 24. Вторая теорема Вейерштрасса.
Пусть
.
Тогда
![]()
Замечание: Непрерывная на отрезке функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу.
Доказательство:
По
условию теоремы
=>
ограничена
на
=>
![]() Докажем, что
Докажем, что
![]() .
Предположим противное, то есть
.
Предположим противное, то есть
![]()
![]() .
Рассмотрим вспомогательную функцию
.
Рассмотрим вспомогательную функцию
![]() на
.
По 1 теореме Вейерштрасса
на
.
По 1 теореме Вейерштрасса
![]() ограничена
на
,
то есть
ограничена
на
,
то есть
![]() .
.
![]()
![]()
![]() (<
)-
верхняя граница.
(<
)-
верхняя граница.
![]() ,
то есть
,
то есть
![]() .
.
Противоречие.
Следствие:
если
![]() ,
то
,
то
![]() .
.
БИЛЕТ 25. Равномерная непрерывность и непрерывность в точке. Теорема Кантора (без доказательства).
Определение 1: Функция непрерывна в точке , если .
Определение 2: Функция непрерывна в точке , если , .
Определение 3: Функция непрерывна в точке , если
.
Функция, непрерывная на отрезке.
Определение:
Функция
называется
непрерывной на отрезке
![]() ,
если она непрерывна в каждой внутренней
точке этого отрезка, непрерывна справа
в точке
,
если она непрерывна в каждой внутренней
точке этого отрезка, непрерывна справа
в точке
![]() и
непрерывна слева в точке
и
непрерывна слева в точке
![]() .
.
Теорема
Кантора:
Если функция
непрерывна
на отрезке
,
то для любого
![]() можно указать такое
,
что
можно указать такое
,
что
![]() для любых
для любых
![]() и
и
![]() из
таких, что
из
таких, что
![]() .
.
+ БОНУС
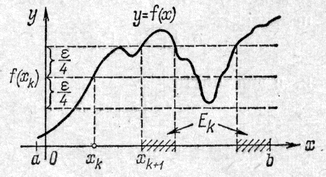
Доказательство:
Возьмем
число
.
Построим на отрезке
точки
![]() следующим образом: если точка
следующим образом: если точка
![]() уже построена, то рассмотрим множество
уже построена, то рассмотрим множество
![]() ,
состоящее из всех точек
,
удовлетворяющих неравенствам:
,
состоящее из всех точек
,
удовлетворяющих неравенствам:
![]() ,
,
![]() .
.
Положим (см. рисунок), что:
![]()
если пусто (и на этом построение заканчивается).
если не пусто.
Заметим,
что
![]() в силу непрерывности
и
в силу непрерывности
и
![]() для любого
из отрезка
для любого
из отрезка
![]() .
Последовательность
.
Последовательность
![]() может быть конечной или бесконечной.
Предположим, что она бесконечна, тогда
для
всех
.
Пусть
может быть конечной или бесконечной.
Предположим, что она бесконечна, тогда
для
всех
.
Пусть
![]() .
Так как
.
Так как
![]() ,
то функция
непрерывна в точке
,
то функция
непрерывна в точке
![]() слева,
и потому можно указать такое число
слева,
и потому можно указать такое число
,
что
![]() и
и
![]() для любого
из интервала
для любого
из интервала
![]() .
По определению числа
можно
найти
.
По определению числа
можно
найти
![]() в
интервале
.
Тогда любое число
из интервала
в
интервале
.
Тогда любое число
из интервала
![]() принадлежит
интервалу
,
и потому
принадлежит
интервалу
,
и потому
![]()
![]()
![]() ,
что противоречит тому, что
,
что противоречит тому, что
![]() .
Таким образом, последовательность
не
может быть бесконечной, и потому
существует такой номер
.
Таким образом, последовательность
не
может быть бесконечной, и потому
существует такой номер
![]() ,
что
,
что
![]() .
Положим:
.
Положим:
![]() .
Возьмем два любых числа
.
Возьмем два любых числа
и
из отрезка
таких, что
![]() .
Тогда возможны два случая: или обе эти
точки попали на некоторый отрезок
.
Тогда возможны два случая: или обе эти
точки попали на некоторый отрезок
![]() и тогда
и тогда
![]() ,
или этого не случилось, и тогда найдется
точка
между
и
.
Но в этом случае
,
или этого не случилось, и тогда найдется
точка
между
и
.
Но в этом случае
![]() ,
так как
,
так как
![]() и (доказывается аналогично)
и (доказывается аналогично)
![]() ,
а потому
,
а потому![]() .
Так как все приведенные рассуждения
справедливы для любого
,
то теорема доказана.
.
Так как все приведенные рассуждения
справедливы для любого
,
то теорема доказана.
Смысл
этой теоремы
состоит в том, что для всех точек отрезка
можно по заданному числу
подобрать общее для всех точек
число
![]() (фигурирующее в определении). Для функций,
непрерывных на интервале это можно
сделать уже не всегда.
(фигурирующее в определении). Для функций,
непрерывных на интервале это можно
сделать уже не всегда.
БИЛЕТ 26. Дифференцируемость функции. Дифференциал. Понятие производной функции.
Определение:
Пусть функция f(x)
определена в окрестности точки
![]() .Если
ее приращение
.Если
ее приращение
![]() можно представить в виде
можно представить в виде
![]() ,то
говорят ,что f(x)
дифференцируема в точке
(иногда
пишут
,то
говорят ,что f(x)
дифференцируема в точке
(иногда
пишут
![]() -величина
более высокого порядка, чем
-величина
более высокого порядка, чем
![]() а это означает, что
а это означает, что
![]() )
)
![]() -линейная
функция от
-линейная
функция от
![]() .Она
называется дифференциалом функции f(x)
и обозначается
.Она
называется дифференциалом функции f(x)
и обозначается
![]()
Пример:
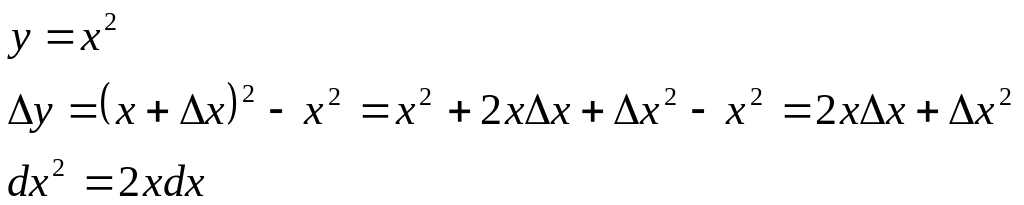
Критерий дифференцируемости:
Для того, чтобы функция y=f(x) была дифференцируема в точке необходимо и достаточно, чтобы существовала производная в этой точке.
Доказательство:
1.Необходимость.
f(x)
дифференцируема в точке
это означает
![]() .
Разделим это равенство на
и перейдем к пределу
.
Разделим это равенство на
и перейдем к пределу
![]()
![]() ,т.е. существует
,т.е. существует
![]() ,
т.е. производная существует.
,
т.е. производная существует.
2.Достаточность.
Пусть существует
![]() или
или
![]() ,
т.е. f(x)
дифференцируема в точке
.
,
т.е. f(x)
дифференцируема в точке
.
Итак,
![]() ,
т.е.
,
т.е.
![]() .Отсюда
следует новое обозначение производной
.Отсюда
следует новое обозначение производной
![]() и эту величину можно рассматривать как
один символ, так и как частное
дифференциалов.
и эту величину можно рассматривать как
один символ, так и как частное
дифференциалов.
Понятие производной функции.
Определение:
Производной функции
![]() в
точке
называется предел
в
точке
называется предел
![]() Очень удобна более короткая запись для
этого предела и более короткое обозначение
для производной
Очень удобна более короткая запись для
этого предела и более короткое обозначение
для производной
![]() .
.
БИЛЕТ 27. Алгебраические свойства дифференцируемых функций.
Теорема:
Если
функции
![]() и
и
![]() имеют
производные, то
имеют
производные, то
1)
![]() .
.
2)
![]() .
.
3)
![]() (
(![]() постоянная).
постоянная).
4)
![]() .
.
Доказательство:
По теореме об арифметике пределов
функций, по определению производной и
формулам:
![]() ,
,
![]() и
и
![]() имеем:
имеем:
1).![]()
![]()
![]() .
.
2).
![]()
=![]() =
=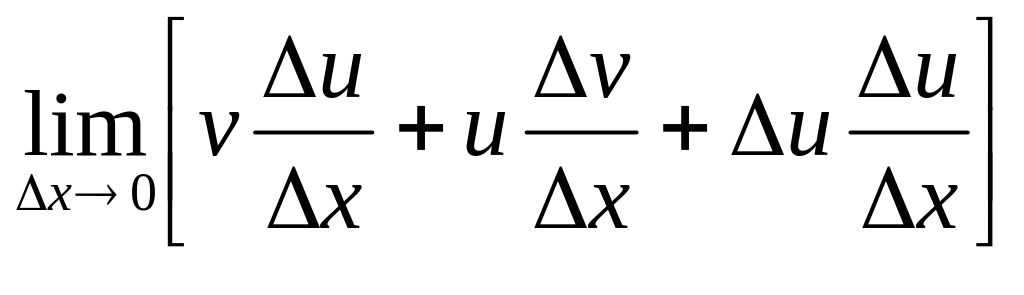 =
=![]()
![]() +
+![]()
![]() +
+
+![]() =
=![]() =
=![]() ,
так как множители
и
не зависят от
и
при
,
так как множители
и
не зависят от
и
при
![]() являются постоянными, а
являются постоянными, а
![]() ,
поскольку
имеет производную и потому непрерывна.
,
поскольку
имеет производную и потому непрерывна.
3).
![]() (так как
(так как
![]() ).
).
4).
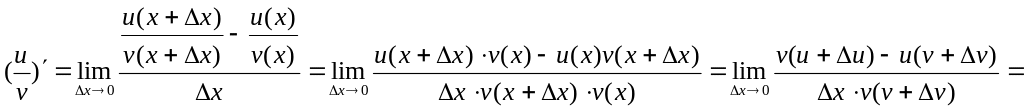 =
=![]()
![]()
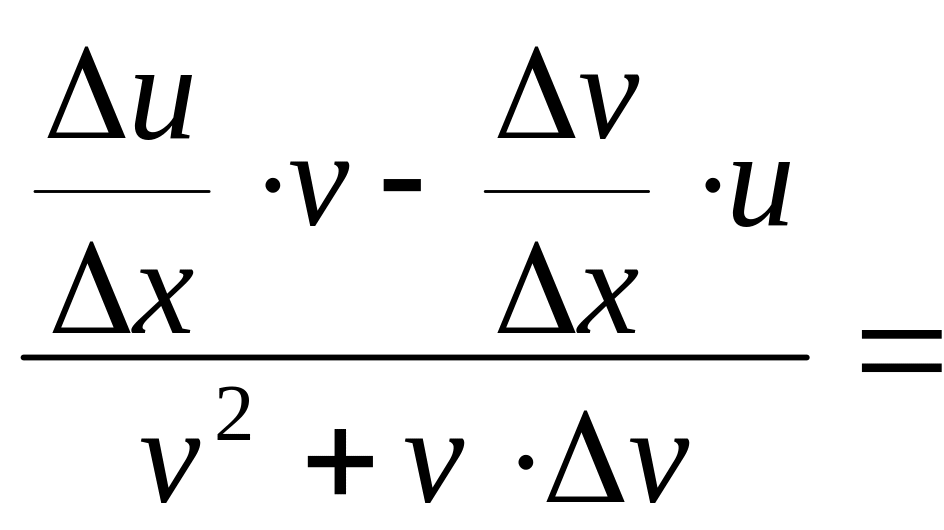
![]() .
.
БИЛЕТ 28. Дифференцирование сложной функции. Инвариантность формы первого дифференциала.
Производная сложной функции.
Пусть
функция y=f(x)
имеет производную в точке
,а
функция z=F(y)
имеет производную в точке
![]() ,
тогда сложная функция Ф(x)=F(f(x))
имеет производную в точке
,
тогда сложная функция Ф(x)=F(f(x))
имеет производную в точке
![]() .
.
Доказательство:
Функция f(x)
непрерывна в окрестности точки
,
функция F(y)
непрерывна в окрестности точки
![]() ,
поэтому в окрестности точки
существует сложная функция Ф(x).Функция
F(y)
имеет производную в точке
,
поэтому она дифференцируема в этой
точке.
,
поэтому в окрестности точки
существует сложная функция Ф(x).Функция
F(y)
имеет производную в точке
,
поэтому она дифференцируема в этой
точке.
![]() (\/)
(\/)
![]() -бесконечно
малая более высокого порядка, чем
-бесконечно
малая более высокого порядка, чем
![]() ,
но
,
но
![]() может быть неопределенна в точке
=0,
поэтому мы доопределяем ее по непрерывности
в точке 0 :
может быть неопределенна в точке
=0,
поэтому мы доопределяем ее по непрерывности
в точке 0 :
![]() .Разделим
равенство (\/) на
:
.Разделим
равенство (\/) на
:
![]()
F(y)=F(y(x))=Ф(x)
и тогда равенство запишем в виде
![]() .
Перейдем к пределу
.
Перейдем к пределу
![]() .
окажем, что
.
окажем, что
![]() ,
то y=f(x)
непрерывна в окрестности точки
,
т.е.
,
то y=f(x)
непрерывна в окрестности точки
,
т.е.
![]() (
и
стремятся
к 0 одновременно), т.е.
(
и
стремятся
к 0 одновременно), т.е.
![]() (т.к.
бесконечно
малая более высокого порядка, чем
),
а
(т.к.
бесконечно
малая более высокого порядка, чем
),
а
![]() ,
т.о. получим формулу
.
,
т.о. получим формулу
.
Инвариантность формы первого дифференциала.
Дифференциал первого порядка имеет тот же самый вид: произведение производной функции на дифференциал аргумента , независимо от того, является аргумент независимой переменной или зависимой.
z-независимая переменная , y-зависит от x
![]()
![]()
Если
y=f(x),
то
![]()
![]()
БИЛЕТ 29. Теорема Ферма.
Теорема Ферма (необходимое условие extr):
Пусть
определена на интервале (a,b)
и точка
![]() если
в точке
если
в точке
![]() функция f(x)
достигает max
или min
значения и в точке
существует производная, то f’(
)=0.
функция f(x)
достигает max
или min
значения и в точке
существует производная, то f’(
)=0.
Доказательство.
Пусть
для определенности в точке
принимает max
значение, т.е
![]() .
В точке
существует производная
.
В точке
существует производная
![]() ,
тогда
,
тогда
![]() (правая
и левая производная).Распишем отношение
(правая
и левая производная).Распишем отношение
![]()
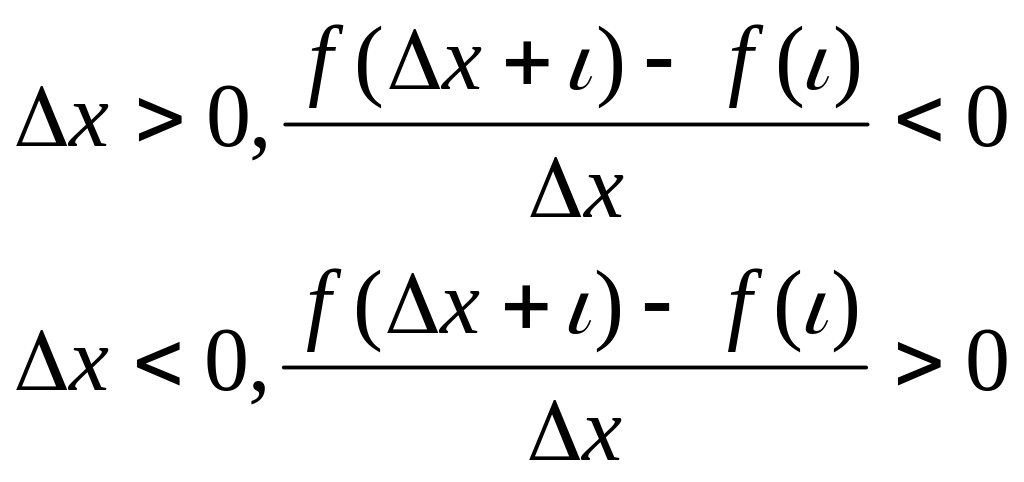 переходя
в этих интервалах к пределу, получим
переходя
в этих интервалах к пределу, получим
![]()
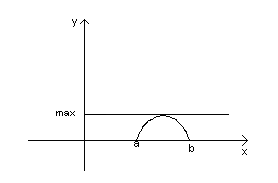
Замечание.
Теорема носит локальный характер, т.е. точка является локальным экстремумом.
Геометрический смысл теоремы.
В предположение теоремы всегда существует точка, в которой касательная к графику функции параллельная OX.
БИЛЕТ 30. Теорема Ролля.
Теорема Ролля:
Пусть функция y= :
1) непрерывна на отрезке [a,b];
2) дифференцируема (a,b);
3)
f(a)=f(b),
тогда
![]()
Доказательство.
Функция
f(x),
непрерывна на [a,b]
достигает на нем max
M
и min
m
значения, т.е
![]() .
Возможны два случая.
.
Возможны два случая.
1)
![]() и
и
![]()
2)
![]() ,тогда
либо максимальное значение f(x)
либо минимальное значения f(x)
достигается внутри интервала (a,b)
(не на конце отрезка [a,b]).(f(a)=f(b)).
,тогда
либо максимальное значение f(x)
либо минимальное значения f(x)
достигается внутри интервала (a,b)
(не на конце отрезка [a,b]).(f(a)=f(b)).
![]() ,
тогда
достигает максимального или минимального
значения во внутренней точке интервала
(a,b) и по
теореме Ферма
,
тогда
достигает максимального или минимального
значения во внутренней точке интервала
(a,b) и по
теореме Ферма
![]()
|
|
|
|
|
|
Все
условия теоремы Ролля существенные.
Если выполняется, только 2 из 3(см.
картинку), то не существует точка причем
![]() (касательная
параллельная оси ОХ).
(касательная
параллельная оси ОХ).
БИЛЕТ 31. Теорема Лагранжа (формула конечных приращений).
Теорема Лагранжа.
Пусть функция f(x)
-непрерывна на отрезке [a,b];
-дифференцируема на интервале (a,b);
Тогда
![]() (формула
конечных приращений)
(формула
конечных приращений)
Доказательство.
Рассмотрим
функцию
![]() .Параметр
.Параметр
![]() выберем из условия F(a)=F(b)
выберем из условия F(a)=F(b)
![]()
![]()
Функция
F(x)
удовлетворяет всем условием т.Ролля
(она непрерывна и дифференцируема, как
сумма непрерывных и дифференцируемых
функций )
![]()
![]()
![]()
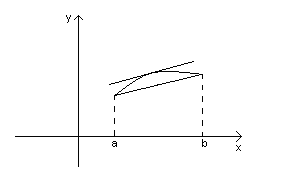
Геометрический смысл.
В
предположение теоремы существует точка![]() :касательная к графику функции параллельна
секущей(хорде).
:касательная к графику функции параллельна
секущей(хорде).
Следствие.
Пусть
f(x)
определена, непрерывна и дифференцируема
на (a,b).
И в каждой точке интервала (a,b)
![]() ,
тогда f(x)=const.
,
тогда f(x)=const.
Доказательство.
Пусть
x1
и x2
две произвольные точки интервала(a,b),тогда
![]() ,
точка
лежит между этими точками x1
и x2,
по условию
,
точка
лежит между этими точками x1
и x2,
по условию
![]() ,
т.е f(x)=const(в
силу произвольности выбора x1
и x2).
,
т.е f(x)=const(в
силу произвольности выбора x1
и x2).
БИЛЕТ 32. Теорема Коши (обобщенная формула конечных приращений).
Теорема Коши.
Пусть функции и g(x) определены на интервале (a,b)
1) и g(x) непрерывны на [a,b];
2)
и g(x)
дифференцируемы на (a,b)
причем
![]() ,
тогда
,
тогда
![]()
Доказательство.
Рассмотрим
функцию
![]() параметр
выбрали из условия
параметр
выбрали из условия
![]()
![]()
![]() .
.
Для
функции F(x)
выполнены условия теоремы Ролля.
Формулировка теоремы Ролля
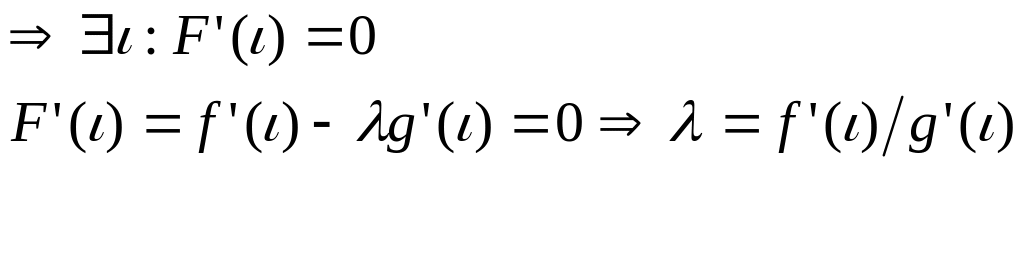 Сравнивания формулы для
,
получим утверждение теоремы.
Сравнивания формулы для
,
получим утверждение теоремы.
Следствие.
Теорема
Лагранжа.
Если
![]() ,то
,то
![]() .
.
БИЛЕТ 33. Правила Лопиталя раскрытия неопределенностей.
Правило Лопиталя.
Для
раскрытия неопределенности вида
![]() .Пусть
и g(x)
определены в окрестности точки а, кроме,
быть может, самой точки а и
.Пусть
и g(x)
определены в окрестности точки а, кроме,
быть может, самой точки а и
![]() .
И пусть в окрестности точки а существуют
.
И пусть в окрестности точки а существуют
![]() .
Если существует
.
Если существует
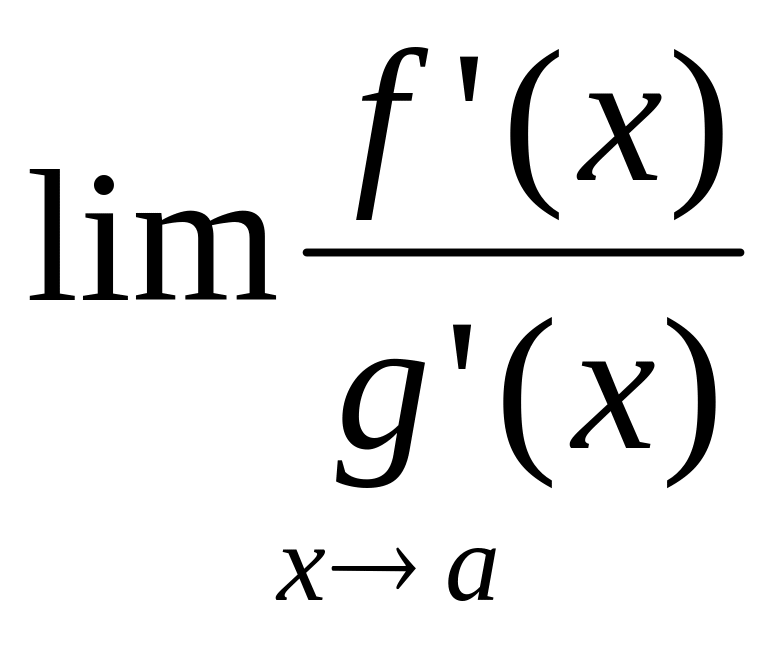 ,
то
,
то
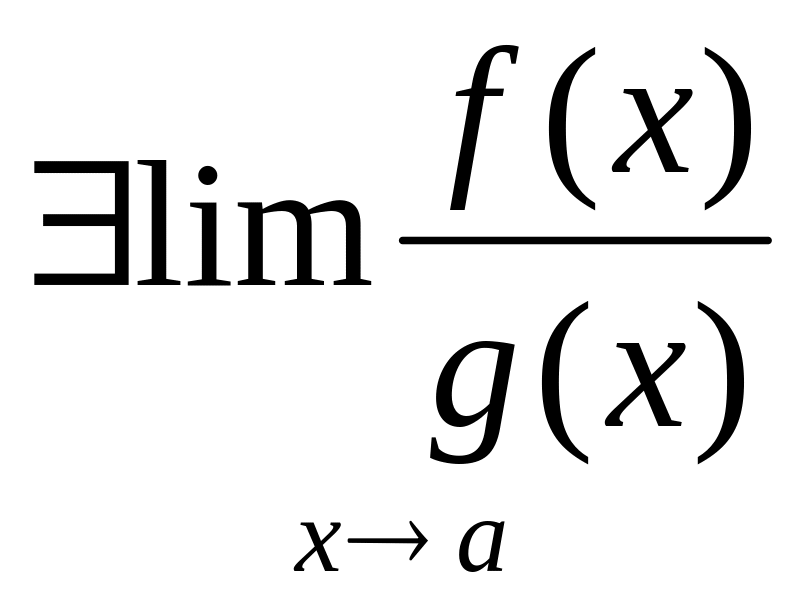 и эти пределы равны.
и эти пределы равны.
Доказательство.
а - конечное число. Доопределим функции и g(x) в точке х=а, по непрерывности: f(a)=g(a)=0. Рассмотрим отношение
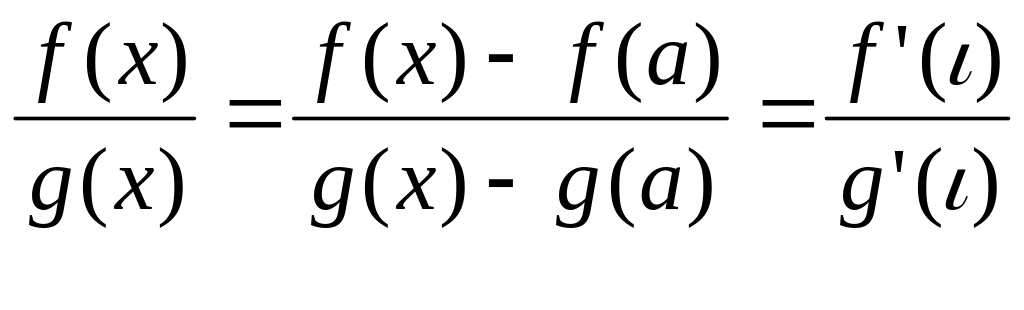 .
Здесь
.
Здесь
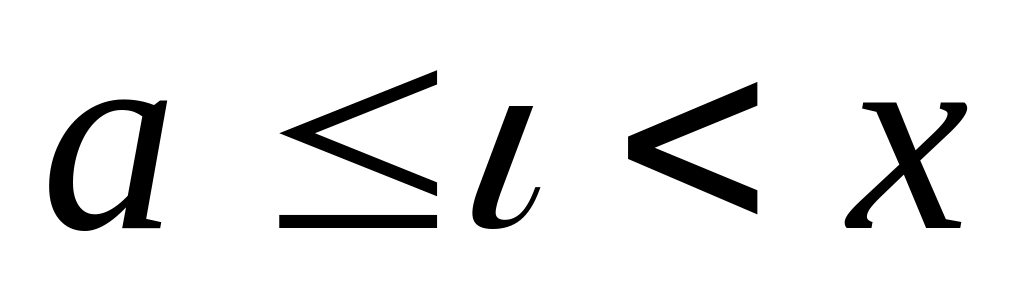 (использовали
теорему Коши). Перейдем к пределу при
(использовали
теорему Коши). Перейдем к пределу при

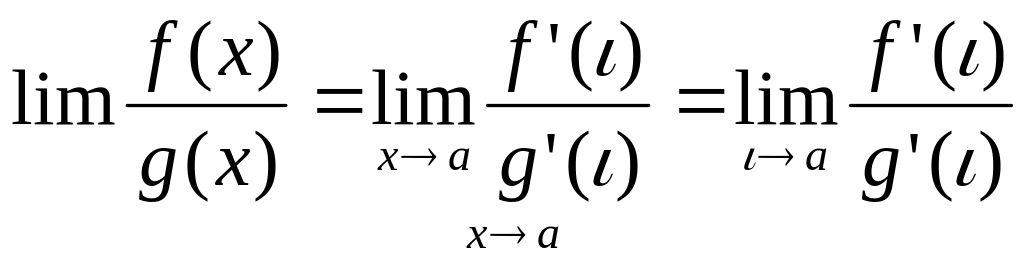 (т.к
(т.к
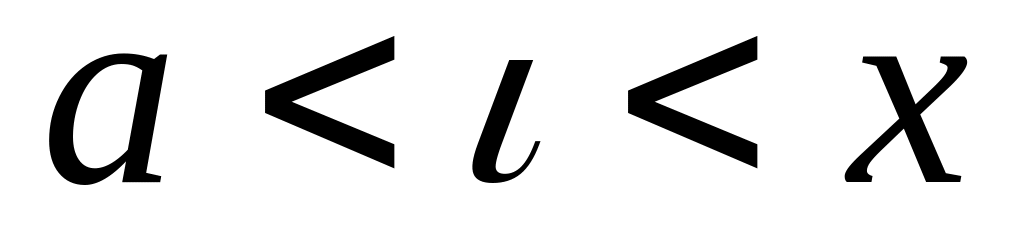 и если
,
то
и если
,
то
 ).
).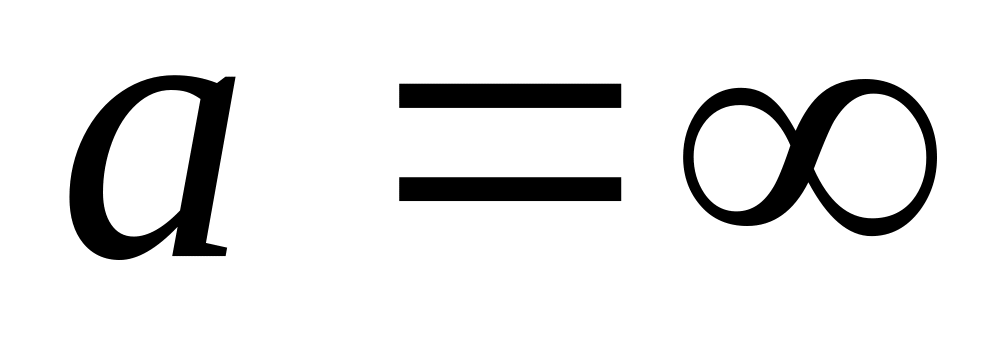 надо
сделать замену, x=1/t,
тогда
надо
сделать замену, x=1/t,
тогда
 ,
,
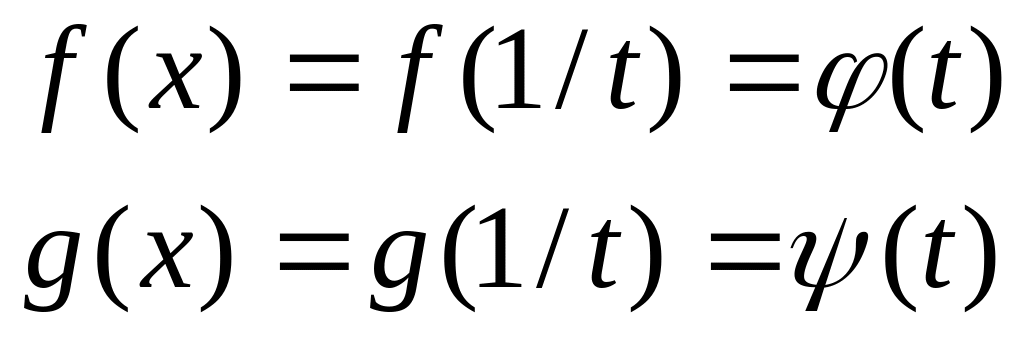
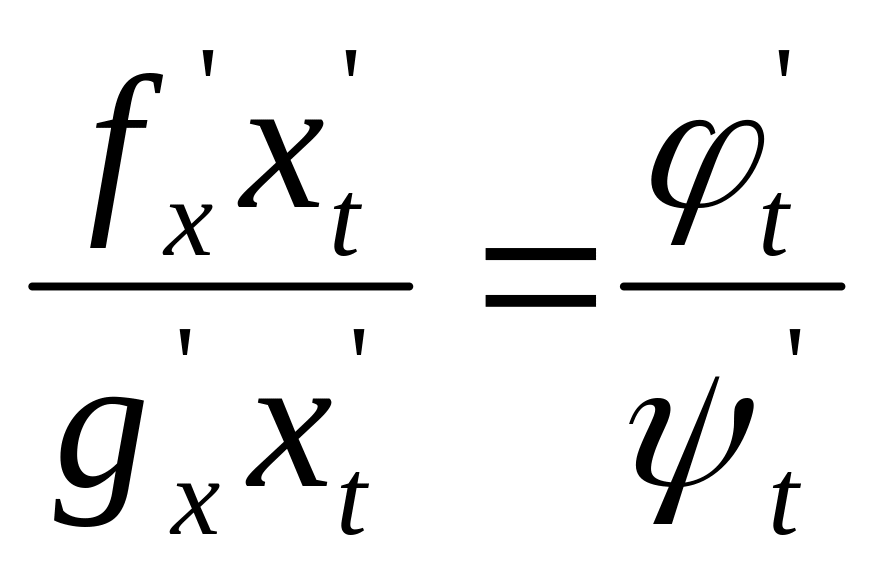 и правило применяется к новой функции
и правило применяется к новой функции
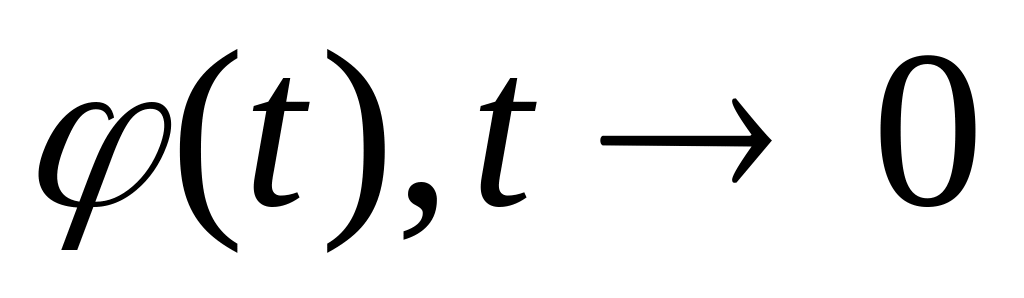
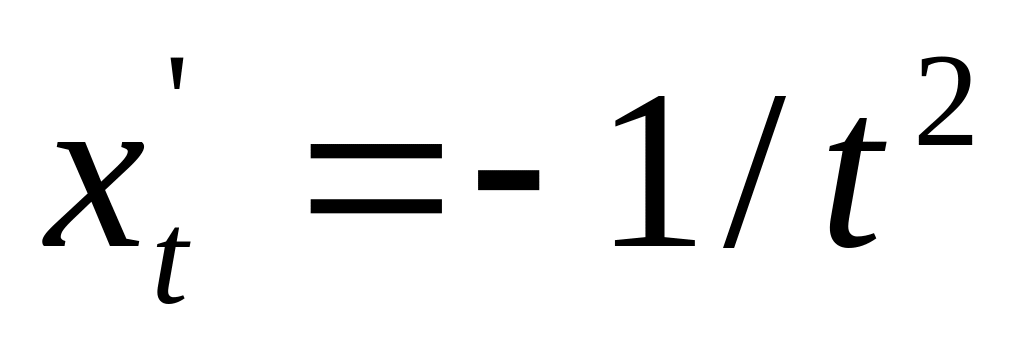 .
.
Теорема 2.
Пусть
и g(x)
определены и дифференцируемы в окрестности
точки а и
![]() .Если
.Если
![]() ,
то
и они равны.
,
то
и они равны.
Замечание.
В формулировке теорем необходимо потребовать, чтобы .
![]() -теорема
1 доказана.
-теорема
1 доказана.
![]() -теорема 2 формулировка.
-теорема 2 формулировка.
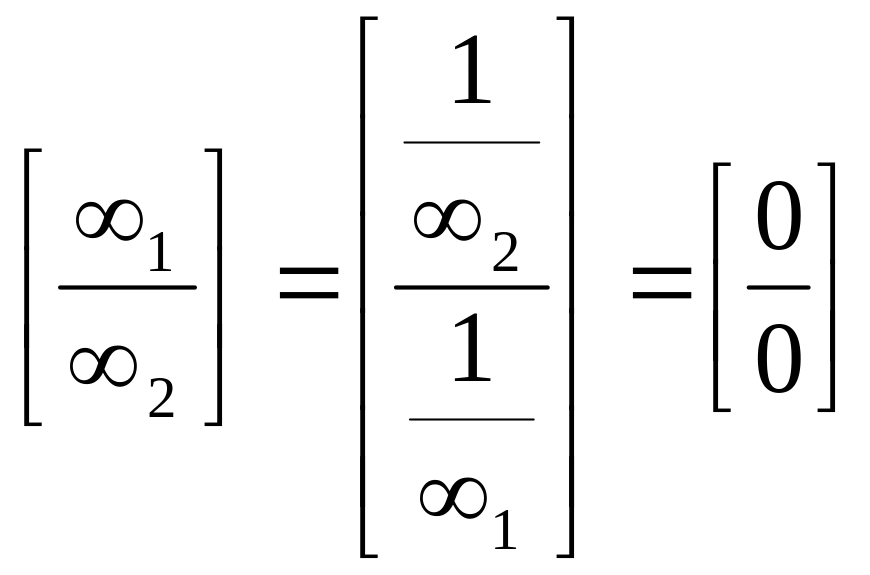
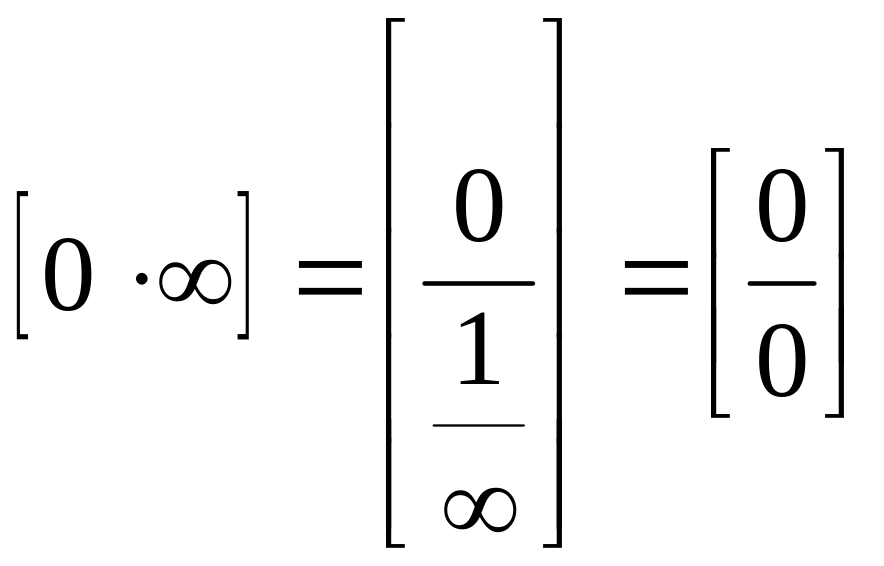
![]()
![]() .
.
Пример,
когда нельзя применять правило Лопиталя
![]() .
.
Вычислим
предел отношения производных
![]() он не существует, т.к. не существует
предел числителя и знаменателя. Правило
Лопиталя применять нельзя.
он не существует, т.к. не существует
предел числителя и знаменателя. Правило
Лопиталя применять нельзя.
Вычислить.
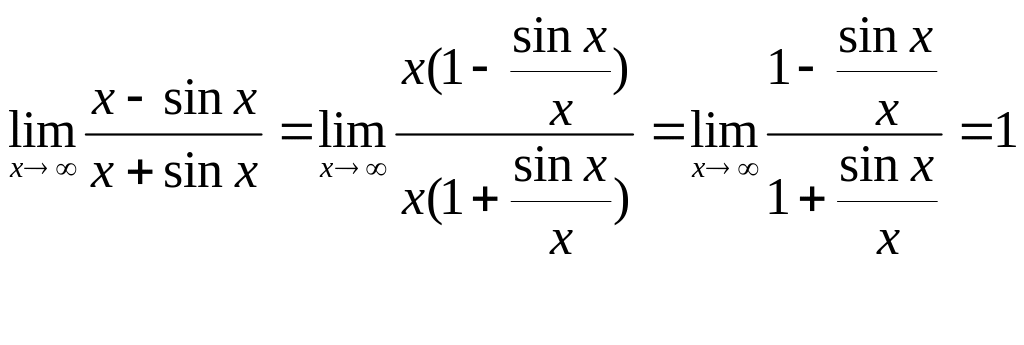
БИЛЕТ 34. Формула Тейлора.
Формула Тейлора.
Пусть
функция
дифференцируема
в точке
,
тогда
![]() ,
где
,
где
![]() -бесконечно
малая более высокого порядка чем
.
-бесконечно
малая более высокого порядка чем
.
![]() ,
где
,
где
![]() линейная
функция, причем
линейная
функция, причем
![]() .
.
Можно
расписать, что
![]() ,
т.е в окрестности точки
функция f(x)
ведет себя как линейная. Поставим более
общую задачу: для функции y=f(x)
найти многочлен порядка n,
который обладает следующими свойствами:
,
т.е в окрестности точки
функция f(x)
ведет себя как линейная. Поставим более
общую задачу: для функции y=f(x)
найти многочлен порядка n,
который обладает следующими свойствами:
![]()
Многочлен
![]() будем писать в виде
будем писать в виде
![]()
первые
равенства получаются путем дифференцирования
формулы для
и подстановки
![]() .
Вторые равенства - это требуемые свойства
.
Вторые равенства - это требуемые свойства
![]() .f(x)
у которого существует производная до
n
порядка включительно можно найти
коэффициенты
.f(x)
у которого существует производная до
n
порядка включительно можно найти
коэффициенты
![]()
Многочлен
,![]() ,
,
![]() многочлен
Тейлора для функции f(x).
многочлен
Тейлора для функции f(x).
Обозначим
![]()
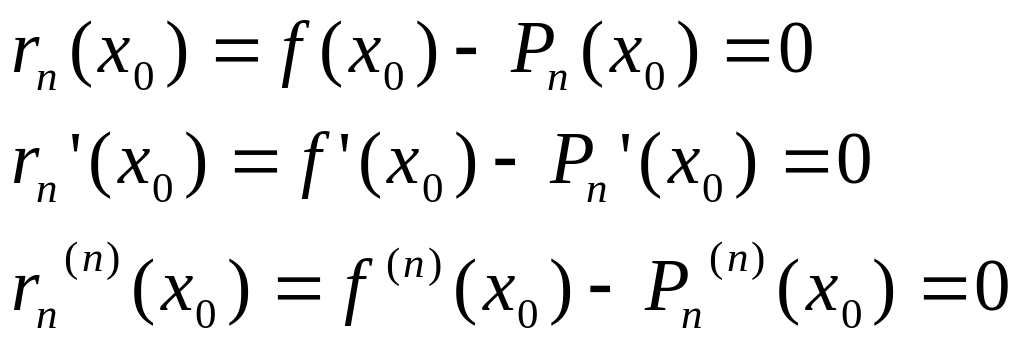
Рассмотрим
функцию
![]() и
вычислим
и
вычислим
Т.о
получим
![]() ,
,![]() остаточный
член формулы Тейлора.
остаточный
член формулы Тейлора.
Пусть
функцияf(x)
определена на интервале (a,b)
и в каждой точке x0
принадлежащей интервалу (a,b)
имеем производную до n
порядка включительно, тогда
,
где
![]()
Единственность многочлена Тейлора.
Пусть
функция
представлена в окрестности точки
многочлена вида
![]()
![]()
Доказательство.
Если
![]() где
её многочлен Тейлора и есть у нас другой
многочлен
где
её многочлен Тейлора и есть у нас другой
многочлен
![]()
![]() надо показать, что коэффициенты одинаковы
надо показать, что коэффициенты одинаковы
![]()
Пусть
![]() сократим на
сократим на
![]()
![]() .
пусть
.
пусть
![]() сократим на
и т.д.
сократим на
и т.д.
![]() многочлен
Тейлора единственен.
многочлен
Тейлора единственен.
БИЛЕТ 35. Условие постоянства функции. Условие монотонности функции.
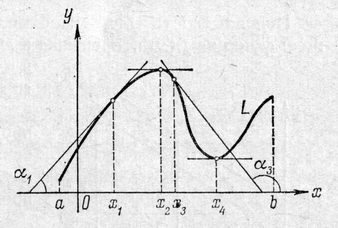
На
рисунке нарисован график
![]() функции
,
всюду имеющей производную. В точке
функции
,
всюду имеющей производную. В точке
![]() касательная к
и ось
касательная к
и ось
![]() образуют
острый угол
образуют
острый угол
![]() ,
поэтому ее угловой коэффициент, равный
,
поэтому ее угловой коэффициент, равный
![]() ,
положителен. Но
,
положителен. Но
![]() .
Следовательно,
.
Следовательно,
![]() .
И так будет в любой точке интервала
.
И так будет в любой точке интервала
![]() ,
где функция
монотонно возрастает. Напрашивается
вывод: если на интервале
,
где функция
монотонно возрастает. Напрашивается
вывод: если на интервале
![]() ,
то на этом интервале функция монотонно
возрастает. Далее, в точке
,
то на этом интервале функция монотонно
возрастает. Далее, в точке
![]() касательная к
образует с осью
тупой
угол
касательная к
образует с осью
тупой
угол
![]() ,
поэтому ее угловой коэффициент, равный
,
поэтому ее угловой коэффициент, равный
![]() отрицателен. А так как
отрицателен. А так как
![]() ,
то
,
то
![]() .
Вывод: если на интервале
.
Вывод: если на интервале
![]() ,
то на этом интервале функция монотонно
убывает. В точке
,
то на этом интервале функция монотонно
убывает. В точке
![]() функция имеет максимум. На чертеже ясно,
что в этой точке касательная к
параллельна оси
,
и поэтому ее угловой коэффициент равен
нулю, так что
функция имеет максимум. На чертеже ясно,
что в этой точке касательная к
параллельна оси
,
и поэтому ее угловой коэффициент равен
нулю, так что
![]() .
При этом слева от этой точки
,
а справа
.
.
При этом слева от этой точки
,
а справа
.
Теорема (достаточный признак монотонности).
1).
Если
![]() на
отрезке
на
отрезке
![]() ,
то
,
то
![]() монотонно
возрастает на
.
монотонно
возрастает на
.
2).
Если
![]() на
отрезке
,
то
монотонно
убывает на
.
на
отрезке
,
то
монотонно
убывает на
.
Доказательство:
Возьмем
любые числа
и
,
причем
<
,
из интервала
.
По формуле Лагранжа получаем:
![]() ,
,
![]() ,
и поэтому
принадлежит интервалу
.
Так как
,
и поэтому
принадлежит интервалу
.
Так как
![]() ,
то в первом случае
,
то в первом случае
![]() ,
то есть
,
то есть
![]() ,
а во втором
,
а во втором
![]() ,
то есть
,
то есть
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
БИЛЕТ 36. Экстремумы функции. Достаточные условия экстремума.
Теорема 1. Необходимое условие экстремума.
Пусть точка х0 является точка экстремума для функции f(x). Тогда, если существует f’(x0), то f’(x0)=0, либо f’(x0) не существует.
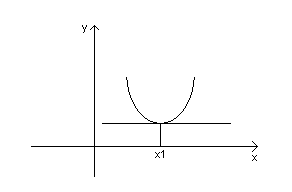
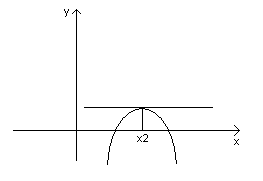
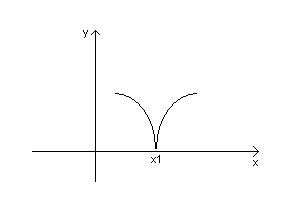
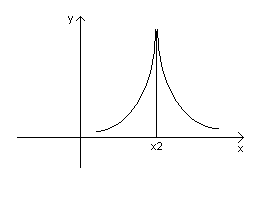
В точке х1 – min; в точке х2 – max.
Теорема 2. Достаточное условие строгого extr в терминах первой производной.
Пусть
f(x)
дифференцируема в некой окрестности
точки х0, и в точке х0 f(x)
непрерывна. Если f’(x)
при переходе через точку х0 меняет знак,
то точка х0 является точкой строгого
экстремума, при этом 1)если при
![]() ,
а при
,
а при
![]()
то
в точке х0 – минимум. 2)если при
![]() ,
а при
,
а при
![]() то в точке х0 максимум.
то в точке х0 максимум.
Доказательство.
Докажем
1)
![]() .Теорема
Лагранжа
.Теорема
Лагранжа
![]() .
а) Если х-х0>0 и
.
а) Если х-х0>0 и
![]() .
б) если х-х0<0 и
.
б) если х-х0<0 и
![]() ,
т.е при переходе через точку х0
,
т.е при переходе через точку х0
![]() не меняет свой знак:
>0,
т.е точка х0-точка минимума.
не меняет свой знак:
>0,
т.е точка х0-точка минимума.
2)Доказательство аналогично.
Достаточное условие строгого экстремума в терминах старшей производной.
Пусть
в точке х0 у функции f(x)
существует n
производных, причём
![]() Тогда, если n=2k,
то в точке х0 экстремум, и если
Тогда, если n=2k,
то в точке х0 экстремум, и если
![]()
![]() Если n=2k+1
в точке х0 нет экстремума и точка х0 точка
возрастания. Если
Если n=2k+1
в точке х0 нет экстремума и точка х0 точка
возрастания. Если
![]()
![]() и точка убывания,
и точка убывания,
![]() если
если
![]() .
.
Следствие.
Если в точке х0 у функции f(x)
существует![]() , то, если
>0,
то в точке х0 минимум,
<0,то
в точке х0 максимум (k=1).
, то, если
>0,
то в точке х0 минимум,
<0,то
в точке х0 максимум (k=1).
Доказательство.
Разложим функцию f(x) в ряд Тейлора.
![]() или
или
![]() знак
определяется
первым слагаемым, если n
– четное, то знак
зависит от знака
знак
определяется
первым слагаемым, если n
– четное, то знак
зависит от знака
![]() .
По этому, если
то
>0
– минимум.
то
<0
– максимум. Если n
– нечетное, то знак
зависит от
и
.
По этому, если
то
>0
– минимум.
то
<0
– максимум. Если n
– нечетное, то знак
зависит от
и
![]() ,
т.е. при переходе через точку х0 знак
меняется, следовательно в точке х0
экстремума нет.
,
т.е. при переходе через точку х0 знак
меняется, следовательно в точке х0
экстремума нет.
Следствие.
![]() .
f’’(x0)>0,
>0
– минимум; f’’(x0)<0,
<0
– максимум.
.
f’’(x0)>0,
>0
– минимум; f’’(x0)<0,
<0
– максимум.
БИЛЕТ 37. Направление выпуклости графика функции. Точки перегиба. Необходимое условие перегиба.
Выпуклости функции. Точка перегиба.
Опр. Функция f(x) на интервале (a,b) называется выпуклой вверх (выпуклой вниз), если
![]()
![]() (
(![]() )
)
Геометрически это означает что кривая y=f(x) лежит выше(ниже) прямой.

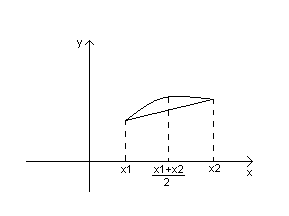
Достаточное условие строго выпуклости.
Теорема. Если на интервале (a,b) f’’(x)>0, то f(x) выпукло вниз, если f’’(x)<0, то f(x) выпукло вверх.
Доказательство
![]()
Рассмотрим
разность
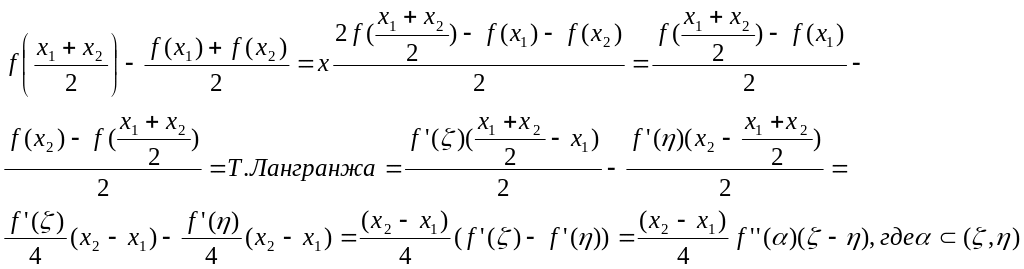 х2-х1>0
х2-х1>0
![]()
а)Если
![]() выпукла вниз.
выпукла вниз.
б)
Если
![]() выпукла вверх.
выпукла вверх.
Опр.
Точка х0 для функции f(x)
называется точкой перегиба, если она
является концом интервала выпуклота
вверх(вниз) и началом интервала выпуклота
вниз(вверх)
![]()
Необходимое условие точек перегиба.
Если функция дважды непрерывна, дифференцируема в точке х0 и если точка х0 является точкой перегиба, то f’’(x0) = 0
Доказательство. Если бы f’’(x0)>0 то в некоторой окрестности точке х0 f(x) была выпукла вниз. Если бы f’’(x0)<0 то в некоторой окрестности точке х0 f(x) была выпукла вверх. Но это противоречит определению точке перегиба: точка перегиба не принадлежит ни какому интервалу выпуклости.
БИЛЕТ 38. Достаточные условия перегиба графика функции.
Достаточное условие точки перегиба.
Если функция f(x) дважды дифференцируема в некоторой окрестности точке х0 кроме, быть может, самой точки х0, но f(x) непрерывна в точке х0 и ее производная меняет знак при переходе через точку х0, то в точке х0 – точка перегиба.
Доказательство.
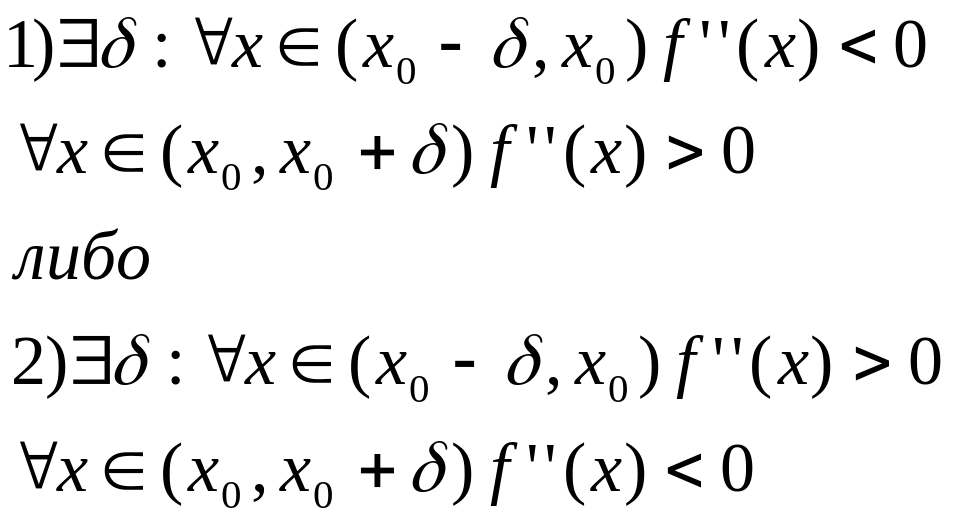
Т.е. в случае (1) точка х0 является концом интервала выпуклости вверх и началом интервала выпуклости вниз, следовательно точка х0 точка перегиба. В случае (2) точка х0 является концом интервала выпуклости вниз и началом интервала выпуклости вверх, следовательно х0 точка перегиба.
Замечание. Заметим, что если функция y=f(x) выпукла вниз, то ее график лежит выше касательной, если функция y=f(x) выпукла вверх, то ее график лежит ниже касательной.
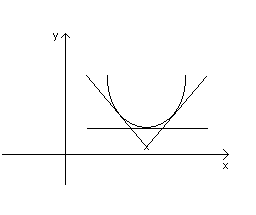
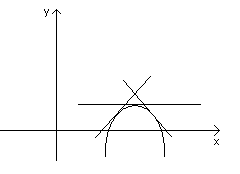
Теорема.
Пусть функция f(x)
обладает следующим условием
![]() непрерывна в точке x0
и
непрерывна в точке x0
и
![]() .n-четное
y=
f(x)
выпукла вверх, если
.n-четное
y=
f(x)
выпукла вверх, если
![]() и выпукла вниз, если
и выпукла вниз, если
![]() ,
n+1-нечетное-
точка x0-точка
перегиба.
,
n+1-нечетное-
точка x0-точка
перегиба.
Доказательство.
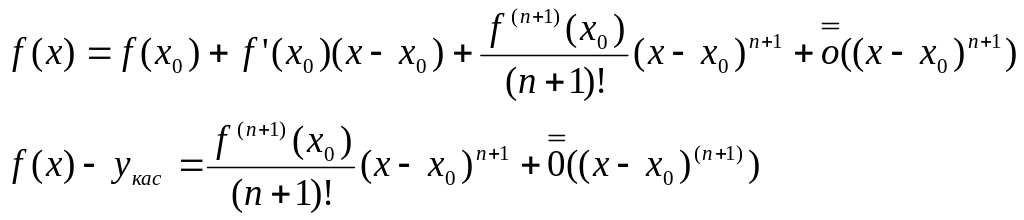
n+1-
четное следовательно положение функции
у нас зависит только от производной
![]() .
N-нечетное
y(x)>y(кас),
если
.
y(x)<y(кас),
если
.
N-нечетное
y(x)>y(кас),
если
.
y(x)<y(кас),
если![]() ,
точка X0-точка
перегиба.
,
точка X0-точка
перегиба.
БИЛЕТ № 39. дифференциальное уравнение первого порядка, их общее частное особое решение
Определение. Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков искомой функции.
Определение. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких переменных – то уравнением в частных производных.
Рассмотрим
пример. Найти
первообразную
![]() ,
если
,
если
![]() .
.
Решение.
Раньше мы
эту задачу решали с помощью неопределенного
интеграла. Однако, ее можно рассматривать
как задачу о нахождении функции
,
удовлетворяющей уравнению
.
![]() .
.
В общем случае дифференциальное уравнение можно записать в виде:
![]() .
(12.1)
.
(12.1)
Например:
![]() .
.
Определение. Дифференциальное уравнение -го порядка называется разрешенным относительно старшей производной, если оно имеет вид:
![]() ,
(12.2)
,
(12.2)
где
![]() - некоторая функция от
- некоторая функция от
![]() переменной.
переменной.
Определение.
Решением
дифференциального уравнения (12.1)
называется такая функция
![]() ,
которая при подстановке ее в это уравнение
обращает его в тождество.
,
которая при подстановке ее в это уравнение
обращает его в тождество.
Например,
![]() есть решение уравнения
есть решение уравнения
![]() ,
т.к.
,
т.к.
![]() .
.
Определение. Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования этого дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.
Пример.
Решить уравнение:
![]() .
.
Решение.
Поскольку
![]() ,
то
,
то
![]() .
Интегрируя левую и правую часть равенства,
получим
.
Интегрируя левую и правую часть равенства,
получим
![]() .
Т.к.
.
Т.к.
![]() ,
то разделив переменные имеем
,
то разделив переменные имеем
![]() .
Интегрируя вторично, получим решение:
.
Интегрируя вторично, получим решение:
![]() ,
,
![]() .
.
Проверка:
![]() .
.
Определение.
Общим
решением
дифференциального уравнения (12.1)
–го
порядка называется такое его решение
![]() ,
которое является функцией переменных
и
произвольных постоянных
,
которое является функцией переменных
и
произвольных постоянных
![]() .
.
Определение. Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных .
Например,
для уравнения
![]()
![]() ,
где
,
где
![]() .
.