1. Общее понятие функции. Числовые множества. Расширенная числовая прямая. Промежутки действительных чисел. Определение числовой функции. Область определения и множество значений функции. Способы задания функции, ее график.

Функция —  закон или правило, согласно которому каждому элементу х ставится в соответствии один определенный элемент из множества.

Основными числовыми множествами являются:

Множество натуральных чисел ℕ= {1;2;3;...; n;....  }

Множество целых чисел Z= {±1;±2;±3;...; ±n;....  }

Множество рациональных чисел Q=

Множество действительных (или вещественных) чисел ℝ.

Все эти множества связаны между собой соотношениями N ⊂ Z ⊂ Q ⊂ R.

Расширенная числовая прямая   (читается «эр с чертой») — множество вещественных чисел  , дополненное двумя элементами:   (положительная бесконечность) и   (отрицательная бесконечность), то есть

Б есконечности   и  , которые не являются числами в обычном понимании этого слова, также называют бесконечными числами, в отличие от вещественных чисел  , называемых конечными числами. При этом для любого вещественного числа   по определению полагают выполненными неравенства

Числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел   или множества комплексных чисел  .

X⊂R, Y=R , где X – область определения функции, Y – область значений функции. Функция задана, если

1. Указана область определения

2. Дан закон f: {(x,y)}, x∈X.

Способы задания функции.

1. Аналитический (с помощью формулы)

2. Графический

3. Табличный

4. Программный

5. Описательный

2. Классификация функций по свойствам.

1. Четные, нечетные, ни четные ни нечетные

Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).

Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).

2. Ограниченные, неограниченные

Функция называется  ограниченной, если существует такое положительное число M, что |  f ( x ) |    M  для всех значений  x . Если такого числа не существует, то функция -неограниченная.

3. Периодические, непериодические

Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода). Формально говоря: если существует положительное число T>0, такое что на всей области определения функции выполняется равенство f(x)=f(x+T). Наименьшее из этих чисел называется периодом функции.

4. Монотонные

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

3. Основные элементарные функции. Понятия сложной и обратной функций. Элементарные функции и их классификация.

Функции, полученные с помощью четырех арифметических действий (сложение, вычитание, умножение, деление) или конечного числа композиций основных элементарных функций, называются элементарными.

Основные элементарные функции – функции вида:

1. Постоянные

2. Степенные

3. Показательные

4. Логарифмические

5. Тригонометрические

6. Обратная тригонометрические

Пусть задана функция y=f(x) с областью определения D и множеством значений Е. Если каждому значению y ∈ E соответствует единственное значение x ∈ D, то задана функция x=φ(y) c областью определения E и множеством значений D. Такая функция x=φ(y) называется обратной к функции y=f(x).

Пусть функция y=f(u) определена на множестве D₁, а функция u=φ(x) определена на множестве D, причем для каждого

x ∈ D соответствующее значение u= φ(x) ∈ D₁. Тогда на множестве D задана функция y=f(φ(x)), которая называется сложной функцией от x ∈ D.

К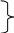 лассификация элементарных функций.

1. Многочлены

2. Дробно-рациональные функции 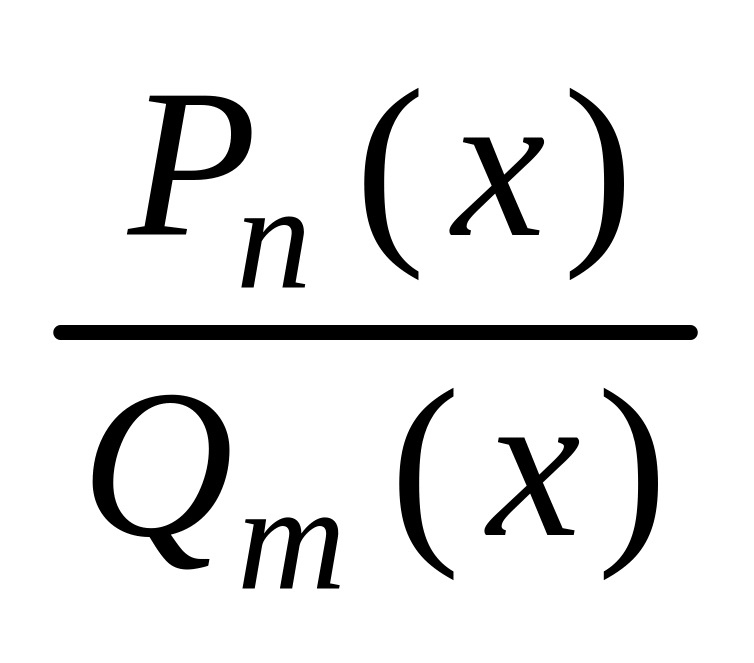Рациональные функции

3. Иррациональные функции – функции, полученные с помощью 4 арифметических действий над рациональными композициями этих функций, но со степенным показателем функции.

4. Трансцендентные— аналитические функции, не являющиеся алгебраическими. Простейшими примерами трансцендентных функций служат показательная функция, тригонометрические функции, логарифмическая функция.

4. Функция от натурального аргумента (числовая последовательность). Пределы функции в точке и на бесконечности; предел числовой последовательности. Односторонние пределы функции в точке, их связь с пределом функции в точке.

Пусть множество   — это либо множество вещественных чисел  , либо множество комплексных чисел  . Тогда последовательность   элементов множества   называется числовой последовательностью.

Число именуется пределом функции при , если для любого числа существует такое число , что из неравенства следует неравенство .

С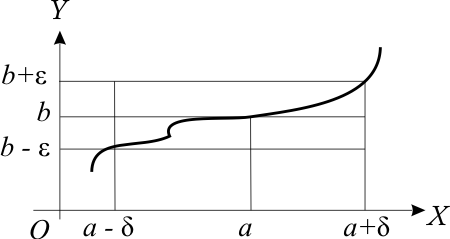 имволическая запись этого определения такова :

.

Геометрическое истолкование предела функции в точке даётся следующим образом. Имеем , то этот предел является единственным. Действительно, по определению функции при наличии двух пределов график функции не мог бы располагаться сразу внутри двух полос: , если .

Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта:

Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так:

Число a называется пределом числовой последовательности x_n, если

Заметим, что здесь использованы логические символы: квантор всеобщности ∀ (вместо слова "для любого") и квантор существования ∃ (вместо слова "найдется").

Предел числовой последовательности обозначается или x_n→ a при. Последовательность, имеющая предел, называется сходящейся, в противном случае расходящейся.

Если при стремлении x к a переменная x принимает лишь значения, меньшие a или большие a и при этом f(x) стремится к A, то говорят, что существуют односторонние пределы функции, то есть lim_x® a-0f(x) = A – предел слева или lim_x® a+0f(x) = A – предел справа. Очевидно, что если lim_x® a-0f(x) = lim_x® a+0f(x) = A, то lim_x® a = A. Верно и обратное утверждение.