Определение аналитической функции комплексной переменной, свойства.
Аналити́ческая функция (действительного переменного) — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.
Свойства
Арифметические свойства
Если 
и 
аналитичны
в области 
Функции
, 
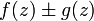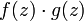и 
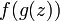аналитичны
в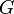 
.Если в области не обращается в ноль, то
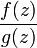будет
аналитична в
Если
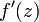в
области
не
обращается в ноль, то 
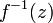будет
аналитична в
.
Аналитическая функция бесконечно дифференцируема в своей области аналитичности. Обратное в общем случае неверно.
Некоторые свойства аналитических функций близки к свойствам многочленов, что, впрочем, и неудивительно — определение аналитичности в смысле Вейерштрасса свидетельствует о том, что аналитические функции — в некотором роде предельные варианты многочленов. Допустим, согласно основной теореме алгебры любой многочлен может иметь нулей числом не более его степени. Для аналитических функций справедливо аналогичное утверждение, вытекающее из теоремы единственности в альтернативной форме:
Если множество нулей аналитической в односвязной области функции имеет в этой области предельную точку, то функция тождественно равна нулю.
Интегрирование функций комплексной переменной. Дифференцирование Определение
Производная
для комплексной функции одного
аргумента 
определяется
так же, как и для вещественной:
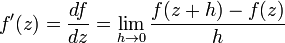
(здесь 
—
комплексное число). Если этот предел
существует, функция
называется дифференцируемой или голоморфной.
При этом
Следует
учитывать одну важную особенность:
поскольку комплексная функция задана
на плоскости, существование приведённого
предела означает, что он одинаков при
стремлении к
с
любого направления. Этот факт накладывает
существенные ограничения на вид
функций-компонент 
и
определяет их жёсткую взаимосвязь
(условия
Коши — Римана):
Отсюда
следует, что дифференцируемости
компонент 
и 
недостаточно
для дифференцируемости самой функции.
Более того, имеют место следующие свойства, отличающие комплексный анализ от вещественного:
Всякая дифференцируемая в некоторой окрестности точки комплексная функция дифференцируема неограниченное число раз и аналитична, то есть её ряд Тэйлора сходится к данной функции во всех точках этой окрестности (в литературе наряду с термином аналитическая функция используется также его синоним «голоморфная функция»).
(Теорема Лиувилля): Если функция дифференцируема на всей комплексной плоскости и не является константой, то её модуль не может быть ограничен.
Обе компоненты дифференцируемой комплексной функции являются гармоническими функциями, то есть удовлетворяют уравнению Лапласа:
Любая гармоническая функция может быть как вещественной, так и мнимой компонентой дифференцируемой функции. При этом другая компонента определяется однозначно (из условий Коши — Римана), с точностью до константы-слагаемого.
Таким
образом, любая дифференцируемая
комплексная функция — это функция
вида 
,
где
—
взаимосвязанные гармонические функции
двух аргументов.