Формальное определение

Критической точкой (или особой точкой, или стационарной точкой) непрерывно дифференцируемой функции (отображения)   называется такая точка  , в которой дифференциал   является вырожденным линейным преобразованием соответствующих касательных пространств в точках   и  , то есть размерность образа   меньше  . В координатной записи это означает что ранг матрицы Якоби функции  , составленной из всех частных производных       меньше своего максимально возможного значения  .

Пространства   и   в этом определении могут быть заменены на многообразия   и   таких же размерностей.

Непрерывность функции нескольких переменных.

 

Z = f(x,y) = f(M) называется непрерывной в т.М₀, если она в этой точке определена, т.е.   или  , и  .

Область состоящая только из внутренних точек, называется открытой областью.

Область состоящая из внутренних точек и всех граничных точек, называется замкнутой областью.

Функция называется непрерывной в D, если она непрерывна в каждой внутренней точке этой области.

Функция называется непрерывной в замкнутой области  , если она непрерывна в каждой внутренней точке этой области и на её границе.

Пусть x получает приращение x, а y получает приращение y, тогда z = f(x,y) получает полное приращение z = f(x + x, y + y) – f(x, y).

Функция z = f(x,y) называется непрерывной в точке (x, y), если она в этой точке определена и бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции, т.е. lim z = 0.

Свойства непрерывных функций справедливые для функции одной переменной, аналогично выполняются и для функции, зависящей от нескольких переменных.

В частности, справедлива теорема Вейерштрасса и теорема Коши для функций, непрерывных в замкнутой области.

Если z = f(x,y) непрерывна в замкнутой области  , то

1.                           Функция достигает в этой области своё наименьшее (m) и своё наибольшее (M) значения.

2.                           (x, y)  D:  .

40. Понятия числового ряда, его суммы. Сходящиеся и расходящиеся числовые ряды. Необходимое условие сходимости числового ряда. Действия с числовыми рядами.

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Рассматриваются числовые ряды двух видов

• вещественные числовые ряды — изучаются в математическом анализе;

• комплексные числовые ряды — изучаются в комплексном анализе;

Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.

Числовые ряды применяются в качестве системы приближений к числам.

Определение

Пусть   — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность

каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида

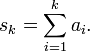
Вообще, для обозначения ряда используется символ

поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.

В соответствии с этим говорится о сходимости числового ряда:

• числовой ряд сходится, если сходится последовательность его частичных сумм;

• числовой ряд расходится, если расходится последовательность его частичных сумм:

• числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.

Если числовой ряд сходится, то предел   последовательности его частичных сумм носит название суммы ряда:

Операции над рядами

Пусть заданы сходящиеся ряды   и  . Тогда:

• Их суммой называется ряд 

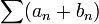
• Их произведением по Коши называется ряд 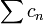 , где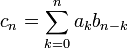 

Если оба ряда сходятся, то их сумма сходится, если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из рядов сходится абсолютно, то произведение рядов сходится.

Сумма числового ряда   определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится^[1]. Элементы ряда   представляют собой либовещественные, либо комплексные числа.

Определение

Пусть   — числовой ряд. Число   называется n-ой частичной суммой ряда  .

Сумма (числового) ряда — это предел частичных сумм  , если он существует и конечен. Таким образом, если существует число  , то в этом случае пишут  . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Сходимость числовых рядов

Свойство 1. Если ряд

   (1.1)

сходится и его сумма равна S, то ряд

  (1.2)

где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.

Свойство 2. Если сходится ряд (1.1) и сходится ряд

,

а их суммы равны   и   соответственно, то сходятся и ряды

,

причём сумма каждого равна соответственно  .

Необходимый признак сходимости ряда

Ряд     может сходиться лишь в том случае, когда член   (общий член ряда) стремится к нулю:

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.

40. Числовые ряды с неотрицательными членами, их свойства. Критерий сходимости, достаточные признаки сходимости числовых рядов: признаки сравнения, признак Даламбера, радикальный признак Коши, интегральный признак Коши. Гармонический ряд.

Ряды с неотрицательными членами

При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.

Теорема. Для сходимости ряда с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.

Признак сравнения рядов с неотрицательными членами.

Пусть даны два ряда и при un, vn  0.

Теорема. Если un  vn при любом n, то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

Доказательство. Обозначим через Sn и n частные суммы рядов и . Т.к. по условию теоремы ряд сходится, то его частные суммы ограничены, т.е. при всех n n  M, где М – некоторое число. Но т.к. un  vn, то Sn  n то частные суммы ряда тоже ограничены, а этого достаточно для сходимости.

Признак сравнения 

     Если   то из сходимости ряда   следует сходимость ряда  , а из расходимости ряда   - расходимость ряда       Предельный признак сравнения 

     Есл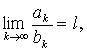и   то при   ряды   и   или оба сходятся, или оба расходятся; при l = 0 из сходимости ряда   следует сходимость ряда  ; при   из расходимости ряда   следует расходимость ряда  . В частности, если   при   то ряды   и   или оба сходятся, или оба расходятся.

Признак Даламбера— признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.

Если для числового ряда

существует такое число  ,  , что начиная с некоторого номера выполняется неравенство

то данный ряд абсолютно сходится; если же, начиная с некоторого номера

то ряд расходится.

Замечание. Среди математиков распространено заблуждение, что "Смех без причины - признак Даламбера". Это не так.

Радикальный Признак Коши

Если для числового ряда

с неотрицательными членами существует такое число  ,  , что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.

Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на  , последний часто может быть найден в явном виде.

Формулировка теоремы

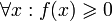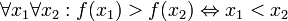Пусть для функции f(x) выполняется:  (функция принимает неотрицательные значения)  (функция монотонно убывает)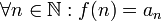  (соответствие функции ряду) Тогда ряд   и несобственный интеграл 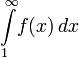  сходятся или расходятся одновременно.

Набросок доказательства

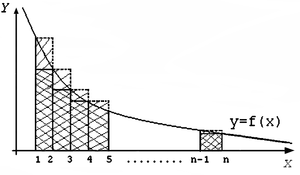
1. Построим на графике f(x) ступенчатые фигуры как показано на рисунке

2. Площадь большей фигуры равна 

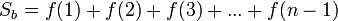
3. Площадь меньшей фигуры равна 

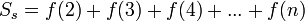
4. Площадь криволинейной трапеции под графиком функции равна 

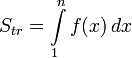
5. Получаем 

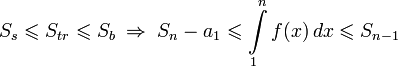
6. Далее доказывается с помощью критерия сходимости знакоположительных рядов.

Гармонический ряд

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда^[1]:

.

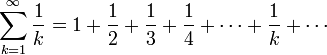Ряд назван гармоническим, так как складывается из «гармоник»:  -я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной   от длины исходной струны.^[2]

Сумма первых n членов ряда

Отдельные члены ряда стремятся к нулю, но его сумма расходится. n-ной частичной суммой s_n гармонического ряда называется n-ное гармоническое число: