ответы на билеты по матану

ДИСКРЕТнАЯ МАТЕМ ATиКА

1. Множества: определение и виды, операции над множествами. Декартово произведение множеств. Мера и норма множеств. Отображения, их свойства, виды. Линейное пространство: определение, виды, базис.

1.Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Специальные множества

• Пустое множество — множество, не содержащее ни одного элемента.

• Универсальное множество (универсум) — множество, содержащее все мыслимые объекты. В связи с парадоксом Рассела данное понятие трактуется в настоящее время как «множество, включающее все множества, участвующие в рассматриваемой задаче».

• Упорядоченное множество — множество, на котором задано отношение порядка.

Сходные объекты

• Набор (в частности, упорядоченная пара) — совокупность конечного числа именованных объектов. Записывается внутри круглых или угольных скобок, а элементы могут повторяться.

• Мультимножество — множество с кратными элементами.

• Пространство — множество с некоторой дополнительной структурой.

• Вектор — элемент линейного пространства, содержащий конечное число элементов некоторого поля в качестве координат. Порядок имеет значение, элементы могут повторяться.

• Последовательность — функция одного натурального переменного. Представляется как бесконечный набор элементов (не обязательно различных), порядок которых имеет значение.

• Нечёткое множество — математический объект, представляющий собой множество, принадлежность к которому представляет собой не отношение, а функцию. Иными словами, относительно элементов этого множества можно говорить «в какой мере» они в него входят, а не просто, входят они в него или нет.

По иерархии

• Множество множеств

• Подмножество

• Надмножество

Бинарные операции

Ниже перечислены основные операции над множествами:

• пересечение:

• объединение:

Если множества  и  не пересекаются,то . Их объединение обозначают также: .

• разность (дополнение):

• симметрическая разность:

• Декартово или прямое произведение:

Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.

Унарные операции

Абсолютное дополнение:

Операция дополнения подразумевает некоторый универсум (универсальное множество , которое содержит ):

Относительным же дополнением называется А\В (см.выше):

• Мощность множества:

Результатом является кардинальное число (для конечных множеств — натуральное).

• Множество всех подмножеств (булеан):

Обозначение происходит из того, что  в случае конечных множеств.

Декартовым произведением множеств A и B называют множество, состоящее из всех упорядоченных пар вида (a; b), где a ∈ A, b ∈ B.

Декартово произведение множеств обозначается A × B. Итак,

A × B = {(a; b) | a ∈ A, b ∈ B}.

Пример: декартово произведение множеств A = {a; b} и B = {1; 2; 3} состоит из пар вида (a; 1), (a; 2), (a; 3), (b; 1), (b; 2), (b; 3), т. е. A × B = {(a; 1), (a; 2), (a; 3), (b; 1), (b; 2), (b; 3)}. Декартово произведение множеств A = {a₁; a₂; …; a_m} и B = {b₁; b₂; …; b_k} записывается в виде таблицы, состоящей из m строк и k столбцов:

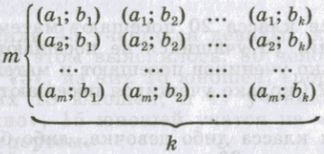(1)

Видно, что если множество A состоит из m элементов, а множество B – из k элементов, то декартово произведение A × B состоит из m * k элементов, т. е. имеет место утверждение:

если A и B – конечные множества, то множество A × B конечно и число его элементов равно произведению n(A) * n(B): n(A × B) = n(A) * n(B).

Отметим, что если в произведении A × B хотя бы одно из множеств A, B пусто, то и произведение A × B = ∅.

Поскольку n(A) * n(B) = n(B) * n(A), то n(A × B) = n(B × A). Однако множества A × B и B × A различны, так как пары (a; b) и (b; a) отличаются порядком элементов.

Хорошо знакомым вам примером декартова произведения множеств является таблица умножения, которая является декартовым произведением множеств

{1; 2; 3; 4; 5; 6; 7; 8; 9} × {1; 2; 3; 4; 5; 6; 7; 8; 9}.

Если A и B – числовые множества, то на координатной плоскости декартово произведение A × B задает некоторое множество точек плоскости с координатами (a; b), где a ∈ A, b ∈ B. Поэтому в паре (a; b) a обычно называют первой координатой, а b – второй координатой.

Можно рассматривать декартово произведение не только двух множеств A и B, а любого конечного числа множеств A₁, A₂, …, A_k: A₁ × A₂ × … × A_k. Элементами такого произведения будут так называемые кортежи (a₁; a₂; …; a_k), где a₁ ∈ A₁, a₂∈ A₂, …, a_k ∈ A_k.

Под отображением множества X в Y будем понимать следующее: каждому элементу X соответствует единственный элемент из Y. Элемент y – образ элемента x, если он соответствует  отображению и обозначается y=f(x); x прообраз y.

Существует три основных вида отображений: инъективное, сюръективное и биективное. Теперь более подробно остановимся на каждом из них.

a) Инъективным отображением множества X на множесто Y называется такое отображение, при котором двум различным элементам из множества X соответствуют различные элементы из множества Y. Другими словами инъективное отображение, если для любых  выполнено .

примером инъективного отображения является отображение: 

б) Сюръективное отображение(или сюръекция). Сюръекцией называется такое отображение, при котором каждому образу из множества Y, соответствует хотя бы один прообраз из множества X/

примером сюръекции является отображение: .

в) Биективное(взаимооднозначное) отображение (или биекция). Биекция является одновременно и инъекцией, и сюръекцией. Поясним это: Для любого образа y из множества Y существует единственный прообраз во множестве X.

примером биекции является отображение: 

Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр

Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из  L линейно выражается через векторы системы.

Иными словами, линейно независимая упорядоченная система векторов e₁, ..., e_n образует базис в L если любой вектор x из L может быть представлен в виде

x = С₁·e₁+С₂·e₂+ ...+С_n· e_n.