7 Конические поверхности.

Определение 7.1. Конической поверхностью с вершиной в точке   называется поверхность, которая вместе с каждой своей точкой  , отличной от точки   содержит прямую  . Прямые, проходящие через вершину конуса и лежащие на нем, называются образующими этого конуса. Отметим, что из определения конуса вовсе не следует, что он имеет единственную вершину. Например, плоскость является конической поверхностью, каждая точка которой может быть принята в качестве вершины. Если какая-нибудь плоскость, не проходящая через вершину конической поверхности и пересекающая все ее образующие, пересекает коническую поверхность по линии  , то эта линия   называется направляющей конической поверхности. Определение 7.2. Функция   называется однородной, если она обладает следующими свойствами: 1. если точка   входит в область определения функции  , то точка  , где   --- любое число, также входит в область определения этой функции. 2. существует такое число  , что для любой точки   из области определения функции   и любого числа  выполняется соотношение Число   называется показателем однородности. ТЕОРЕМА 7.1. Если уравнение  , где   --- однородная функция, в декартовой системе координат является уравнением поверхности, то эта поверхность коническая, причем вершина конуса лежит в начале координат. Доказательство, очевидно. Мы перенесем это определение и на поверхности второго порядка. Если поверхность второго порядка является конической, то ее вершина --- центр этой поверхности, причем лежит на самой поверхности. ТЕОРЕМА 7.2. Для того чтобы поверхность второго порядка, заданная общим уравнением   являлась уравнением конической поверхности с вершиной в начале координат, необходимо и достаточно, чтобы в этом уравнении отсутствовали как члены с первыми степенями координат, так и свободный член, т.е. уравнение такой конической поверхности имело вид:

Доказательство необходимости. Пусть уравнение   является уравнением конической поверхности с вершиной в начале координат. Так как начало координат является вершиной, т.е. центром этой поверхности второго порядка, то по теореме 6.1. уравнение этой поверхности имеет вид Далее, так как вершина конической поверхности лежит на этой поверхности, т.е. начало координат лежит на ней, то из последнего уравнения получаем, что  . Доказательство достаточности очевидно, так как уравнение   однородное относительно  , т.е. вместе с каждой своей точкой содержит и всю прямую, проходящую через начало координат. Уравнение   после приведения к каноническому виду таково: значит, среди поверхностей второго порядка коническими поверхностями являются следующие: 1. мнимый конус второго порядка, если   не равные нулю числа одного знака; 2. действительный конус второго порядка, если   не равные нулю числа одного знака, а   не равное нулю число противоположного знака; 3. две мнимые пересекающиеся плоскости, если   не равные нулю числа одного знака, а  ; 4. две действительные пересекающиеся плоскости, если   не равные нулю числа разных знаков, а  ; 5. две совпадающие плоскости, если  , а  . ТЕОРЕМА 7.3. 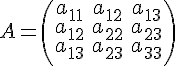Для того чтобы поверхность второго порядка, заданная общим уравнением   являлась уравнением конической поверхности, необходимо и достаточно, чтобы ранги матриц  и 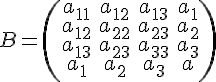 были равны между собой. Доказательство необходимости. Пусть поверхность второго порядка является конической поверхностью с вершиной в точке  . Произведем параллельный перенос системы   так, чтобы новым началом координат стала вершина  данной конической поверхности. Тогда по теореме 7.2. в такой системе координат уравнение поверхности примет вид а матрица   преобразуется в матрицу 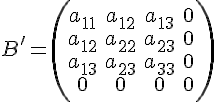Но ранг матрицы   при таком преобразовании не меняется, следовательно, rank  rank  rank Доказательство достаточности. Пусть равны ранги матриц   и  . Тогда равны ранги матриц   и 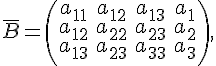 значит, поверхность имеет центр (или даже прямую или плоскость центров). Произведем перенос осей   так, чтобы новым началом координат стал центр поверхности --- точка  . В такой системе координат уравнение примет вид Как уже отмечалось ранг матрицы   при этом не изменится, но   преобразуется в матрицу 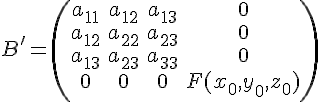Но тогда rank  rank  rank , следовательно,  . Значит центр поверхности лежит на этой поверхности, но этим свойством обладают только конические поверхности. Теорема доказана.