
- •1 Переход от одной декартовой системы координат к другой в пространстве.
- •2 Необходимые сведения из теории квадратичных форм.
- •3 Понятие общего уравнения поверхности второго порядка. Классификация поверхностей второго порядка.
- •4 Теория инвариантов.
- •5 Определение канонического уравнения поверхности второго порядка при помощи инвариантов.
- •6 Центр поверхности второго порядка.
- •7 Конические поверхности.
- •8 Цилиндрические поверхности.
- •9 Пересечение поверхности второго порядка с прямой. Асимптотические направления.
- •Конусы асимптотических направлений.
- •10 Диаметральная плоскость, сопряженная данному неасимптотическому направлению.
- •11 Касательная плоскость.
- •12 Главные направления поверхности второго порядка.
- •13 Число главных направлений поверхностей второго порядка.
- •14 Определение расположения поверхности второго порядка по отношению к декартовой системе координат.
13 Число главных направлений поверхностей второго порядка.
Докажем следующие положения.
1. Если --- простой корень характеристического уравнения , то система имеет ненулевое решение, но не может иметь два линейно независимых решения.
В
самом деле, если бы система
имела
два линейно независимых решения, то
ранг определителя этой системы был бы
ниже
![]() и
потому его производная
и
потому его производная
обращалась бы в нуль при , т.е. кратность корня была бы больше .
2. Если
![]() ,
то ненулевые векторы
,
то ненулевые векторы
![]() и
и
![]() , которые
мы получим из системы
при
и
,
ортогональны друг другу.
, которые
мы получим из системы
при
и
,
ортогональны друг другу.
В самом деле, из соотношений
 и
и
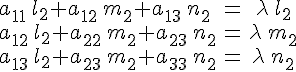 находим
находим
![]() +
+
![]()
![]() +
+
![]() Левые
части этих равенств тождественны,
значит,
Левые
части этих равенств тождественны,
значит,
![]() или
или
![]() и
так как
,
то
и
так как
,
то
![]() ,
а значит
,
а значит
![]() .
.
Из доказанного, а так же из предыдущего параграфа приходим к следующим выводам.
Если все корни характеристического уравнения простые и ненулевые, то поверхность имеет только три попарно перпендикулярных главных направления.
Если
![]() ,
то поверхность имеет одно главное
направление, соответствующее корню
,
и всякое направление, к нему перпендикулярное,
также будет главным.
В этом случае
поверхность второго порядка является
поверхностью вращения.
,
то поверхность имеет одно главное
направление, соответствующее корню
,
и всякое направление, к нему перпендикулярное,
также будет главным.
В этом случае
поверхность второго порядка является
поверхностью вращения.
Если
![]() ,
то любое направление является главным
(сфера).
,
то любое направление является главным
(сфера).
Если
![]() ,
то поверхность имеет два главных взаимно
перпендикулярных направления.
,
то поверхность имеет два главных взаимно
перпендикулярных направления.
Если
![]() ,
то любое направление перпендикулярное
вектору, соответствующему корню
,
будет главным (поверхность вращения).
,
то любое направление перпендикулярное
вектору, соответствующему корню
,
будет главным (поверхность вращения).
Если
![]() ,
то имеется одно главное направление,
соответствующее корню
.
,
то имеется одно главное направление,
соответствующее корню
.
Определение 13.1. Диаметральная плоскость, соответствующая главному направлению называется главной диаметральной плоскостью.
Главные диаметральные плоскости --- это плоскости симметрии поверхности, а главные направления --- это направления прямых, не имеющих асимптотического направления, перпендикулярных к этим плоскостям симметрии.
Замечание 13.1. Все центральные поверхности, не являющиеся поверхностями вращения, имеют по три плоскости симметрии, попарно перпендикулярные друг другу, и по три оси симметрии, имеющие главные направления, перпендикулярные к плоскостям симметрии и проходящие через центр поверхности.
Каждая из центральных поверхностей вращения обладает плоскостью симметрии проходящей через ее центр и перпендикулярной к оси вращения. Кроме того, плоскостями симметрии будут все плоскости, проходящие через ось вращения. Осью симметрии в этом случае будет ось вращения, а также всякая прямая, проходящая через центр поверхности и перпендикулярная к оси вращения. Все оси симметрии идут по главным направлениям.
Эллиптический параболоид, не являющийся параболоидом вращения, и каждый гиперболический параболоид имеют по две перпендикулярные друг другу плоскости симметрии, являющиеся диаметральными плоскостями. Линия их пересечения является осью симметрии поверхности. В отличие от осей симметрии центральных поверхностей ось симметрии параболоида имеет не главное, а особое направление, причем ось симметрии, являющаяся линией пересечения плоскостей симметрии, пересекает параболоид в одной точке --- в его вершине.
Параболоид вращения имеет одну ось симметрии --- ось вращения. Всякая плоскость, проходящая через нее, является главной диаметральной плоскостью.
