3 Понятие общего уравнения поверхности второго порядка. Классификация поверхностей второго порядка.

Определение 3.1. Уравнение

называется общим уравнением поверхности второго порядка в пространстве. Предварительно докажем геометрическим способом одну общую теорему из теории квадратичных форм, а именно для квадратичной формы от трех переменных:

ТЕОРЕМА 3.1. Всякая квадратичная форма от трех переменных однородным ортогональным преобразованием может быть приведена к такому виду (каноническому), чтобы преобразованная форма не содержала членов с произведением новых переменных, взятых попарно. Доказательство. Введем в пространстве ортонормированный базис  . Переменные   рассматриваем как координаты некоторого вектора   в этом базисе. Введем новый ортонормированный базис  . Координаты   произвольного вектора   в базисе   через координаты   того же вектора   в базисе   выражаются соотношениями   предыдущего параграфа. Обозначим это однородное ортогональное преобразование через  . Подставляя в   вместо   их значения из  , получим квадратичную форму  , относительно базиса   (обозначим ее  ) Докажем сначала, что ортонормированный базис   можно выбрать так, что в выражении   обратятся в нуль коэффициенты при   и  . Выписывая из соотношения   половины коэффициентов при   и   и приравнивая их нулю, получим уравнения, которые можно записать в виде Эти соотношения означают, что вектор должен быть ортогонален векторам  и   иначе коллинеарен вектору  , т.е. по признаку коллинеарности векторов имеем систему равенств

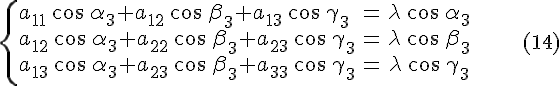
или

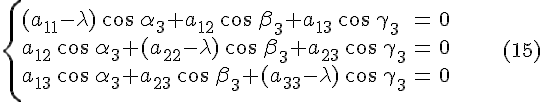
Так как вектор   должен быть единичным и так как система   однородная относительно  , то она имеет ненулевое решение тогда и только тогда, когда определитель этой системы равен нулю:

Это уравнение называется характеристическим уравнением формы  . В данном случае наше уравнение третьей степени относительно  . Так как все коэффициенты квадратичной формы являются действительными числами, то это уравнение имеет по крайней мере один действительный корень. Рассмотрим тот случай, когда уравнение имеет простой действительный корень, который обозначим так:  . Подставляя это значение   в систему  , получим систему 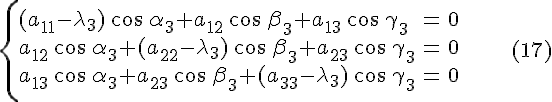Система   не может иметь относительно   два линейно независимых решения, так как тогда бы корень   имел бы кратность больше единицы. В самом деле, если бы существовало два линейно независимых решения, то матрица системы 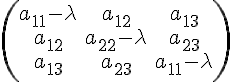 имела бы ранг, меньший двух, и значит, производная от характеристического многочлена 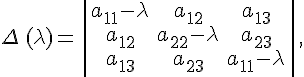 которая равна 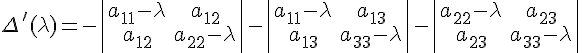обращалась бы в нуль, т.е. корень   имел бы кратность больше единицы, что противоречит нашему предположению. Итак, существуют только два противоположных единичных вектора  и  координаты, которых удовлетворяют системе  . Выбирая любой из них располагая векторы перпендикулярно вектору   и друг другу, получим, что форма   в таком базисе примет вид  Теперь произведем поворот осей системы   вокруг оси   на некоторый угол  ; этому повороту соответствует однородное ортогональное преобразование  которое, как известно, можно выбрать таким, что форма   преобразуется в форму  Таким образом, при однородном ортогональном преобразовании   форма   преобразуется в форму Теорема доказана. Отметим (и это очень важно для дальнейшего), что Отсюда по симметрии, так как форма   не содержит произведений   и  , то   и, аналогично,   , где   --- корни характеристического уравнения  . Таким образом, канонический вид формы   имеет вид где   --- корни характеристического уравнения   формы  . Из доказанного следует также, что: 1. все корни характеристического уравнения действительны; 2. если все корни   --- простые, то, подставляя в систему   вместо   корень  , получим систему из которой можно найти координаты направляющего вектора новой оси   , а при   --- новой оси  ; 3. если   , то форма   имеет вид и при любом ортогональном преобразовании   она не будет менять этого вида. Таким образом, уже при ортогональном преобразовании  форма   перейдет в форму В этом случае система   при   имеет два линейно независимых решения. В качестве направляющих векторов новых осей   и   можно взять любые два, ортогональные вектору   и между собой; 4. Если, наконец,  , то форма   имеет вид а отсюда следует, что форма   с самого начала имеет канонический вид. ТЕОРЕМА 3.2. Общее уравнение

поверхности второго порядка, заданное относительно аффинной системы координат, при помощи преобразования системы координат в прямоугольную систему можно преобразовать к одному из следующих пяти простейших уравнений:

Доказательство. Перейдем сначала от аффинной системы координат к декартовой. При таком переходе порядок поверхности не изменится, а поэтому можно считать, что уравнение   поверхности дано относительно декартовой системы координат с самого начала. По теореме 2.1., существует прямоугольная система координат   такая, что уравнение   преобразуется к виду

где   --- корни характеристического уравнения  . Возможны следующие случаи.

1. Предположим, что в уравнении 

Тогда уравнение   можно переписать в виде

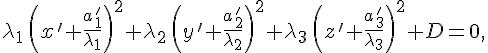
где  . Производя параллельный перенос системы $Ox\,'y\,'z\,'$ так, чтобы новым началом координат была точка  (координаты точки даны относительно системы  ), получим уравнение в системе координат   в виде

2. Предположим, что в уравнении 

Тогда уравнение   можно переписать в виде

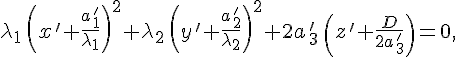
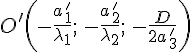где  . Производя параллельный перенос системы   так, чтобы новым началом координат была точка   (координаты точки даны относительно системы  ), получим уравнение в системе координат  в виде

3. Предположим, что в уравнении 

Тогда уравнение   можно переписать в виде

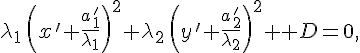
где  . Производя параллельный перенос системы   так, чтобы новым началом координат была точка   (координаты точки даны относительно системы  ), получим уравнение в системе координат  в виде

4. Предположим, что в уравнении 

но хотя бы один из коэффициентов   или   отличен от нуля.

a). Если  , то уравнение   можно представить в виде

 

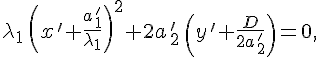
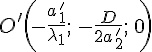где  . Производя параллельный перенос системы   так, чтобы новым началом координат была точка   (координаты точки даны относительно системы   ), получим уравнение в системе координат   в виде

b). Если же  , то при помощи переноса осей координат избавимся от первой степени   и уравнение в некоторой системе   примет вид

где 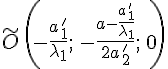 . Производя затем поворот осей   вокруг новой оси   по формулам 

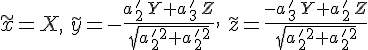
приведем последнее уравнение к виду

5. Наконец, если  , то уравнение   имеет вид  , которое при помощи параллельного переноса начала координат в точку , очевидно, приводится к виду

где  . Теорема доказана.

ТЕОРЕМА 3.3. Общее уравнение

поверхности второго порядка, заданное относительно аффинной системы координат, выражает одну из следующих семнадцати поверхностей, указанных в таблице:

Номер	Название поверхности	Простейшее уравнение
1	Эллипсоид
2	Мнимый эллипсоид
3	Однополостный гиперболоид
4	Двуполостный гиперболоид
5	Конус
6	Мнимый конус
7	Эллиптический параболоид
8	Гиперболический параболоид
9	Эллиптический цилиндр
10	Мнимый эллиптический цилиндр
11	Гиперболический цилиндр
12	Две пересекающиеся плоскости
13	Две мнимые пересекающиеся плоскости
14	Параболический цилиндр
15	Пара параллельных плоскостей
16	Пара мнимых параллельных плоскостей
17	Пара совпавших плоскостей

Доказательство. Согласно двум предыдущим теоремам нужно рассмотреть следующие случаи: 1. Пусть поверхность принадлежит первой группе, т.е. имеет простейшее уравнение

и пусть  . Тогда

(a) Если числа   одного знака, а   имеет знак им противоположный. В этом случае уравнение   можно переписать в виде

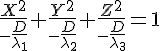
и так как  , то можно положить  , тогда в этих обозначениях получим уравнение эллипсоида.

(b) Если числа   и   одного знака. В этом случае уравнение   можно переписать в виде

и так как  , то можно положить  , тогда в этих обозначениях получим уравнение мнимого эллипсоида.

(c) Если числа   одного знака, а   имеют знак им противоположный. В этом случае уравнение   можно переписать в виде

и так как  , то можно положить  , тогда в этих обозначениях получим уравнение однополостного гиперболоида.

(d) Если числа   одного знака, а   имеет знак им противоположный. В этом случае уравнение   можно переписать в виде

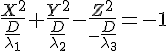
и так как  , то можно положить  , тогда в этих обозначениях получим уравнение двуполостного гиперболоида.

Пусть теперь 

(a) Если числа   одного знака, а   имеет знак им противоположный. В этом случае уравнение   можно переписать в виде 

полагая  , получим уравнение конуса.

(b) Если числа   одного знака. В этом случае уравнение   можно переписать в виде

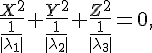
полагая  , получим уравнение мнимого конуса.

2. Пусть поверхность принадлежит второй группе, т.е. имеет простейшее уравнение

Тогда возможны следующие случаи (a) Числа   одного знака. Выбором положительного направления оси   можно добиться того, что коэффициент при   в уравнении   будет иметь знак противоположный знаку  . В таком случае уравнение   переписывается в виде

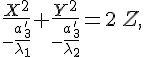
полагая  , получаем уравнение эллиптического параболоида.

(b) Числа   разных знаков. Выбором положительного направления оси   можно добиться того, что коэффициент при   в уравнении   будет иметь знак противоположный знаку  . В таком случае уравнение   переписывается в виде

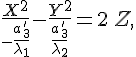
полагая  , получаем уравнение гиперболического параболоида.

Рассмотрение поверхностей, определяемых уравнениями   и   проводится также, как исследовались линии второго порядка.