14 Определение расположения поверхности второго порядка по отношению к декартовой системе координат.

Теория инвариантов для поверхностей второго порядка дает ответ на вопрос о том как выглядит простейшее уравнение этой поверхности. Помимо канонического уравнения поверхности второго порядка надо знать ту систему координат, в которой эта поверхность имеет каноническое уравнение, т.е. знать координаты нового начала и направления осей.

Для центральных поверхностей достаточно найти координаты центра из системы и координаты векторов, имеющих главные направления, из системы 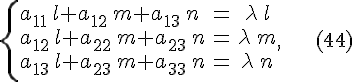где вместо   надо подставлять корни характеристического уравнения.

В случае центральных поверхностей вращения достаточно найти координаты центра и координаты направляющего вектора оси вращения, соответствующего простому корню характеристического уравнения. В случае сферы достаточно определить координаты ее центра и радиус.

ПРИМЕР 14.1. Определить вид и расположение поверхности, заданной относительно декартовой системы координат уравнением Если общее уравнение поверхности второго порядка является уравнением эллиптического или гиперболического цилиндра, вопрос о расположении решается так: уравнения   являются уравнениями места центров (прямая). Направляющий вектор этой прямой определяет направление канонической оси аппликат. Координаты направляющих векторов осей абсцисс и ординат (если это не круговой цилиндр) определяются из системы  , куда надо подставлять ненулевые корни характеристического уравнения. Если цилиндр круговой, то векторы осей абсцисс и ординат выбираются очевидным образом, т.е. перпендикулярно оси аппликат и друг другу.

ПРИМЕР 14.2. Определить вид и расположение поверхности, заданной относительно декартовой системы координат уравнением

Для параболоидов существует лишь одно особое направление, совпадающее с направлением канонической оси аппликат. Однако, в отличии от центральных поверхностей, при определении направления вектора канонической оси аппликат нам нужно знать точное направление, а именно внутрь параболоида. Докажем, что вектор  , координаты которого определяются из системы (как единственное особое направление)

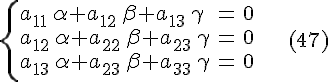
будет направлен внутрь параболоида тогда и только тогда, когда

Действительно, простейшее уравнение параболоида имеет вид 

где  . Сечение параболоида плоскостью   является парабола  . Значит, если  , то ось   направлена внутрь данного сечения.

Оси абсцисс и ординат имеют главные направления.

Осталось определить вершину параболоида. Для этого заметим, что если точка   --- произвольная точка параболоида, то координаты нормального вектора касательной плоскости в этой точке, таковы 

Значит данная точка будет вершиной параболоида тогда и только тогда когда этот вектор будет коллинеарен вектору особого направления, координаты которого находятся из системы  . Тогда имеем 

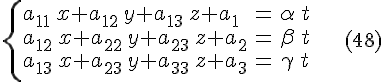
Умножая эти равенства на   и складывая почленно, в силу   получим

Переписывая, уравнение поверхности в виде

в силу соотношений   получим

Таким образом для нахождения вершины параболоида необходимо решить линейную систему   и  .

ПРИМЕР 14.3. Определить вид и расположение поверхности, заданной относительно декартовой системы координат уравнением

Предположим, что поверхность второго порядка является параболическим цилиндром. Пусть

единичные векторы канонической системы координат. Пусть   --- парабола, по которой плоскость  , перпендикулярная к образующим, пересекает поверхность. Тогда векторы   и   компланарны плоскости  , причем   коллинеарен оси параболы  . Рассмотрим однородное ортогональное преобразование

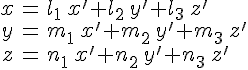
Тогда в системе координат   уравнение нашего цилиндра примет вид

где  .

Дальнейшее упрощение уравнения   производится параллельным переносом, при котором коэффициент   в каноническом уравнении   останется прежним. Поэтому для того чтобы вектор   был направлен внутрь параболы  необходимо и достаточно, чтобы

Направление оси абсцисс является главным. Далее находим главную диаметральную плоскость и линию ее пересечения с поверхностью (образующая, проходящая через новое начало). Определяем направление осей аппликат и ординат.

ПРИМЕР 14.4. Определить вид и расположение поверхности, заданной относительно декартовой системы координат уравнением