1 Переход от одной декартовой системы координат к другой в пространстве.

Введем в пространстве две прямоугольные системы координат   и  . Как известно, координаты единичного вектора в ортонормированном базисе являются косинусами углов между этим единичным вектором и базисными векторами. Обозначим углы между вектором   и векторами   через  ; углы между вектором   и векторами   через  ; углы между вектором   и векторами   через  . Тогда единичные векторы декартовой системы   выразятся через единичные векторы декартовой системы   следующим образом:

Пусть   --- координаты произвольной точки   относительно системы  , а   --- координаты той же точки   в системе  . Тогда

Формулы   задают так называемое однородное ортогональное преобразование системы координат или в более геометрической формулировке замену координатных векторов декартовой системы . Матрица перехода для формул   имеет вид Эта матрица является ортогональной, т.е. сумма квадратов элементов, расположенных в каждом столбце, равна  , а сумма произведений соответствующих элементов двух любых различных столбцов равна нулю. Отметим также, что матрица ортогональна тогда и только тогда, когда  . Отметим частный случай однородного ортогонального преобразования систем координат, когда оси   и   совпадают. В этом случае

и формулы   принимают вид

где   --- угол от оси   до оси   в плоскости  . Наконец, если в пространстве введены две декартовы системы координат   и  , причем   в системе  , то координаты   произвольной точки   относительно системы   выражаются через координаты   той же точки   в системе   соотношениями

Формулы   задают так называемое неоднородное ортогональное преобразование системы координат или по простому переход от одной ПДСК к другой. В частности, если  , то формулы   примут вид

которые задают параллельный перенос системы координат.

2 Необходимые сведения из теории квадратичных форм.

Определение 2.1. Пусть   ---  - мерное векторное пространство над полем действительных чисел. Билинейной формой, определенной на векторном пространстве  , называется отображение   линейное по каждому аргументу. Это значит, что каждой упорядоченной паре векторов   ставится в соответствие действительное число   такое, что выполняются равенства

Возьмем какой-нибудь базис   пространства  . Тогда по определению базиса имеем Следовательно, Используя равенства  , получаем где  . Определение 2.2. Билинейная форма называется симметрической, если для любых векторов   выполняется равенство  . В частности,  . Определение 2.3. Пусть   --- симметрическая билинейная форма на пространстве  . Отображение   по закону   называется квадратичной формой  , определенной на пространстве  . Если   --- какой-нибудь базис пространства  , то

Из коэффициентов   можно составить, очевидно, квадратную матрицу   порядка  ; она называется матрицей квадратичной формы  . Элементы матрицы  , симметричные относительно главной диагонали равны между собой, т.е. матрица   --- симметрическая. Обратно, для любой симметрической матрицы  -го порядка можно указать вполне определенную квадратичную форму  , имеющую элементы матрицы   своими коэффициентами. Заметим, что матрица   тогда и только тогда будет симметрической, если она совпадает со своей транспонированной, т.е если  . Квадратичную форму   можно записать в ином виде, используя умножение прямоугольных матриц. Условимся сначала о следующем обозначении: если дана квадратная или вообще прямоугольная матрица  , то через   будет обозначаться матрица, полученная из матрицы   транспонированием. Если матрицы   и   таковы, что их произведение определено, то имеет место равенство:  , т.е. матрица, полученная транспонированием произведения, равна произведению матриц, получающихся транспонированием сомножителей, притом взятых в обратном порядке. Обозначим теперь через   вектор-столбец, составленный из координат вектора  , т.е. 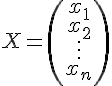 является матрицей, имеющей   строк и один столбец. Транспонируя эту матрицу, получим матрицу состоящую из одной строки. Квадратичная форма   с матрицей   может быть записана теперь в виде следующего произведения:

Что произойдет с квадратичной формой  , если перейдем к другому базису. Пусть   --- еще один базис пространства   , причем 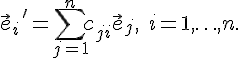Тогда, если   координаты вектора   в базисе  , то имеют место равенства

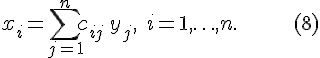
Обозначим через   --- матрицу перехода от базиса   к базису  . Обозначая через  вектор-столбец из координат  , запишем преобразование   в виде матричного равенства:

Отсюда получаем, что

Подставляя   и   в запись   формы  , получим запись квадратичной формы в другом базисе или или где

Матрица   будет симметрической, так как Таким образом, доказана следующая ТЕОРЕМА 2.1. Квадратичная форма, имеющая матрицу  , после перехода к другому базису с матрицей перехода   превращается в квадратичную форму, причем матрицей этой формы служит матрица  .