4 Теория инвариантов.

Произведем над переменными   многочлена второй степени от этих переменных

линейное неоднородное преобразование

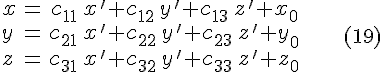
Пусть

многочлен, в который при этом преобразовании перейдет многочлен  . Тогда имеют место соотношения

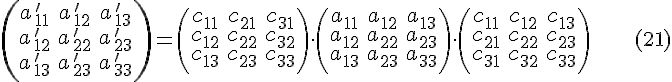
В самом деле, квадратичная форма, входящая в состав функции  , преобразуется в квадратичную форму, входящую в состав функции   при однородном преобразовании

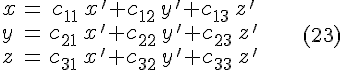
Отсюда формула  . Далее функция   может быть получена из квадратичной формы 

при  , а неоднородное преобразование   получается из однородного 

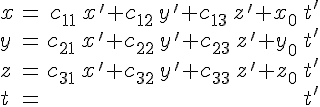
при  . Из этих соображений, учитывая  , получается формула  .

Из соотношений   и   следует, что при любом преобразовании  , имеют место соотношения:

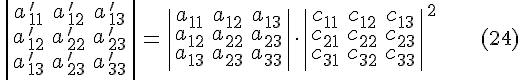
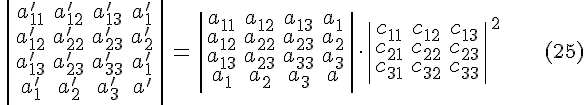
Определение 4.1. Ортогональными инвариантами поверхности второго порядка называются функции от коэффициентов общего уравнения   поверхности второго порядка, значения которых не изменяются при преобразовании декартовой системы координат.

ТЕОРЕМА 4.1. Функции

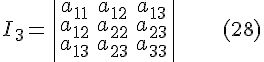
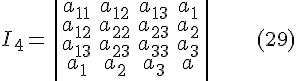
являются ортогональными инвариантами поверхности второго порядка, заданной общим уравнением  , относительно декартовой системы координат.

Доказательство. Так как определитель ортогонального преобразования   равен  , то его квадрат равен   и инвариантность   и   следует из соотношений   и   настоящего параграфа.

Для доказательства того, что   и   также являются ортогональными инвариантами, заметим прежде всего, что коэффициенты  являются инвариантами параллельного переноса:

Это проверяется непосредственной подстановкой   в  . Поэтому достаточно доказать, что   и   являются инвариантами однородного ортогонального преобразования   (замена базисных векторов). При этом преобразовании имеет место соотношение  , так как и правая и левая часть есть квадрат расстояния от одной и той же точки до начала координат. 

Рассмотрим вспомогательную квадратичную форму от трех переменных, которая при каждом   соответствует некоторой поверхности второго порядка 

при однородном ортогональном преобразовании   она перейдет в форму 

По доказанному   является ортогональным инвариантом, значит, имеем равенство 

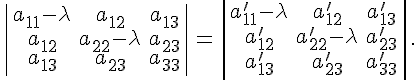
Это равенство верно при всех значениях  , следовательно, равны соответствующие коэффициенты при   и   в левой и правой частях, т.е. 

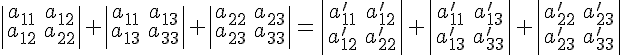
ТЕОРЕМА 4.2. Функции

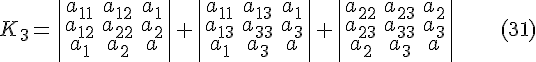
являются инвариантами однородного ортогонального преобразования. Эти функции   и   называются полуинвариантами.

Если же общее уравнение поверхности второго порядка   однородным ортогональным преобразованием может быть приведено к виду

то   является ортогональным инвариантом, а если общее уравнение поверхности второго порядка   однородным ортогональным преобразованием может быть приведено к виду

то   (и, конечно,  ) является ортогональным инвариантом.

Доказательство. Рассмотрим семейство поверхностей второго порядка

Производя однородное ортогональное преобразовании   (замена базисных векторов), получим 

По предыдущей теореме   --- ортогональный инвариант. Используя это по отношению к полученной поверхности, имеем равенство

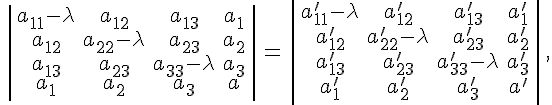
которое является тождеством относительно  .

Приравнивая коэффициенты при коэффициенты при   и   в левой и правой частях, получим требуемое. Первая часть теоремы доказана.

Пусть теперь однородным ортогональным преобразованием общее уравнение поверхности второго порядка   может быть приведено к виду  . Тогда для  полуинвариант   имеет значение

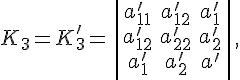
который в свою очередь есть инвариант параллельного переноса. 

Аналогично доказывается инвариантность  .