7.Векторы

     Обозначения:

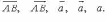
     Длина вектора, модуль (абсолютная величина):

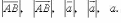
     Сумма векторов:

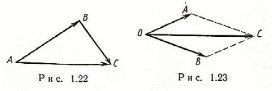
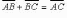      (правило треугольника) (рис. 1.22);

      (правило параллелограмма) (рис. 1.23);

      (правило многоугольника);

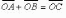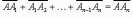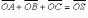      (правило параллелепипеда, 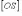- диагональ).

     Разность векторов:

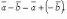
     Формула вычитания векторов: 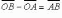(рис. 1.24).

     Признак коллинеарности векторов:

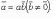
Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,

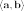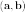или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):

.

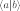Обычно предполагается что скалярное произведение положительно определено, то есть

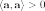для всех .

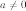Если этого не предполагать, то произведение называется индефинитным.

8.Общее уравнение плоскости в r3

 

Зафиксируем произвольную декартову прямоугольную систему координат O_xyz и рассмотрим произвольное уравнение первой степени

Ах + Ву + Сz + D = 0, (2.1)

где A, B, C, D - произвольные константы, хотя бы одна из которых не равна 0.

Уравнение (2.1) заведомо имеет хотя бы одно решение (x₀, y₀, z₀).

Действительно, пусть С  0, следовательно, взяв произвольные (x₀, y₀), мы получим ,

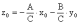то есть существует точка М₀(x₀, y₀, z₀) такая, что

Ах₀ + Ву₀ + Сz₀ + D = 0, (2.2)

которое эквивалентно (2.1).

Рассмотрим разность между (2.1) и (2.2).

Мы получим

А(х - х₀) + В(y - у₀) + С(z - z₀) + D = 0, (2.3)

которое эквивалентно (2.1).

Докажем, что уравнение (2.2) и, стало быть, уравнение (2.1), определяет плоскость (П) в O_xyz.

Пусть вектор

,

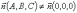то есть хотя бы одна координата его не равна 0.

Возьмем произвольную точку М₀(x, y, z), принадлежащую плоскости П, то есть ее координаты удовлетворяют уравнению (2.3), ибо в этом случае вектор 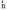перпендикулярен вектору 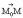( 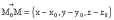) и их скалярное произведение

А(х - х₀) + В(y - у₀) + С(z - z₀) (2.4)

равно нулю.

Если точка М(x,y,z) не принадлежит плоскости П, то ее координаты не удовлетворяют (2.3), ибо в этом случае вектор 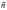не перпендикулярен вектору и (2.3) не равно нулю.

Таким образом, мы доказали следующее утверждение.

 

Теорема 2.1. Если в R³ фиксирована произвольная декартова система координат O_xyz (прямоугольная), то всякое уравнение первой степени с тремя переменными x,y,z определяет относительно этой системы плоскость.

 

 

З а м е ч а н и я.

1. Уравнение (2.1) с произвольными коэффициентами А, В, С (хотя бы один из которых не должен быть равен нулю) называется общим уравнением плоскости в R³.

2. Если два общих уравнения

Ах + Ву + Сz + D = 0

и

А₁х + В₁у + С₁z + D₁ = 0

определяют одну и ту же плоскость, следовательно, существует число t, такое, что справедливы равенства

A₁ = tA, B₁ = tB, C₁ = tC, D₁ = tD.

 

Рассмотреть(самостоятельно) неполные уравнения плоскости, когда

1) А = 0; 2) В = 0; 3) C = 0; 4) D = 0;

5) A = В = 0; 6) A = C = 0; 7) B = C = 0;

8) A = В = C = 0; 9) A = C = D = 0; 10) В = C = D = 0

Гиперплоскость

Гиперпло́скость — подпространство коразмерности 1 в векторном, аффинном пространстве или проективном пространстве; то есть подпространство с размерностью, на единицу меньшей, чем объемлющее пространство.

Например, для двумерного пространства гиперплоскость есть прямая, для трёхмерного — плоскость и т. д.

Уравнение гиперплоскости

Пусть 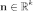 — нормальный вектор к гиперплоскости, тогда уравнение гиперплоскости, проходящей через точку 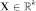, имеет вид

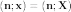
Здесь  — скалярное произведение в пространстве 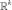. В частном случае уравнение принимает вид

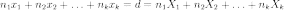
Расстояние от точки до гиперплоскости

Пусть  — нормальный вектор к гиперплоскости, тогда расстояние от точки 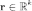до этой гиперплоскости даётся формулой

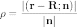
где 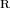 — произвольная точка гиперплоскости.

9.Уравнение прямой в R3

Рассмотрим прямую J с вектором А0А в R3 и коллинеарный ему вектор p(k,l,m)(направляющий вектор). Если точки А0 и А заданы координатами: А0 (x0,y0,z0) , A(x, y, z), то из условия

коллинеарности А0А и p можно записать:

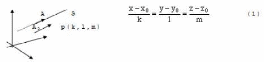
Выражение (1) называют каноническим уравнением прямой в пространстве.

Если ввести параметр t такой, что 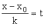, то получим параметрическое уравнение прямой в R3:

х = x0 + kt, y = y0 + kt, z = z0 + kt (2)

Заметим, что прямая J в R3 всегда является пересечением двух плоскостей L1 и L2 . Тогда:

L1 отвечает уравнение A1 x + B1 y + C1 z + D1 = 0,

L2 отвечает уравнение A2 x + B2 y + C2 z + D2 = 0.

с нормалями n1(A1, B1, C1) n2(A2, B2, C2). Вектор р(k,l,m) является направляющим для прямой J, причем выполнены очевидные условия р ^ n1 , p ^ n2 или (р ,n1) = 0, (p, n2) = 0

Из условия р ^ n1 , p ^ n2 следует, что направляющий вектор р является векторным произведением [n1 x n2] = p или

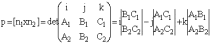
Тогда координаты направляющего вектора р(k,l,m) равны:

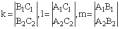
Подставив в уравнение 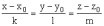 вместо k, l, m их миноры, получим требуемое.

Рассмотри взаимное расположение прямых и плоскостей в R3.

1.Взаимное расположение двух прямых J1 и J2:

Пусть заданы:J1: 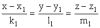, Jр2:

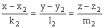
Условие параллельности: ,

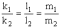условие перпендикулярности: k1k2+ l1l2+ m1m2 = 0

2. Взаимное расположение прямой J и плоскости L:

Пусть заданы: J: 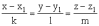, L: Ax + By + Cz + D = 0,

Условие параллельности: Ak + Bl + Cm = 0,

условие перпендикулярности:

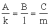
3. Угол a между прямой J и плоскостью L:

Все полученные результаты обобщаются на векторное пространство произвольной размерности. Например, каноническое уравнение прямой J в Rn будет иметь вид:

(х1 – х01)/A1 = (х2 – х02)/A2= …= (хn – х0n)/An

где:(х01,х02…,х0n)и(х1,х2…,хn)–координаты точек Р0 и Р прямой J,

(A1 ,A2, …,An ) – координаты нормали р.

Прямая и плоскость в пространстве. Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью.

 

Отметим, что многие утверждения и формулы, касающиеся плоскости в пространстве, доказываются и выводятся так же, как при изучении прямой на плоскости, поэтому в этих случаях будут даваться ссылки на предыдущую лекцию.

 

Плоскость в пространстве.

 

Получим сначала уравнение плоскости, проходящей через точку М₀(х₀ ,у₀ ,z₀) перпендикулярно вектору n = {A,B,C},называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z) вектор М₀М = {x - x₀ , y - y_{0 ,} z - z₀) ортогонален вектору n, следовательно, их скалярное произведение равно нулю:

A(x - x₀) + B(y - y₀) + C(z - z₀) = 0. (8.1)

Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

После приведения подобных можно записать уравнение (8.1) в виде:

Ax + By + Cz + D = 0, (8.2)

где D = -Ax₀ - By₀ - Cz₀. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.