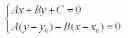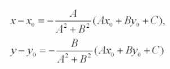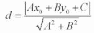- •1.Система координат
- •4.Уравнение прямой, проходящей через две заданные точки
- •5. Нормальное уравнение прямой
- •6.Расстояние от точки до прямой
- •7.Векторы
- •8.Общее уравнение плоскости в r3
- •10.Эллипс
- •11. Гипербола
- •Уравнения
- •Свойства
- •13.«Недекартовые» системы координат в пространстве
- •Полярные координаты
- •14.Сферическая система координат
- •15.Линейное пространство
- •Линейное векторное пространство. Линейное пространство векторов.
- •16.Линейная независимость
- •Определение
- •Свойства
- •Значение
- •17.Базис
- •Происхождение термина
- •Элементарное введение: базис в евклидовой плоскости и пространстве
- •Обозначения
- •Евклидово пространство
- •18.Ортогональность векторов. Перпендикулярность векторов.
- •19.Разложение вектора по базису
5. Нормальное уравнение прямой
Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем, то получим
xcos + ysin - p = 0 – нормальное уравнение прямой.
Знак нормирующего множителя надо выбирать так, чтобы С < 0.
р – длина перпендикуляра, опущенного из начала координат на прямую, а - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение этой прямой в отрезках:
уравнение этой прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой:
; cos = 12/13; sin = -5/13; p = 5.
Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
Уравнение прямой имеет вид: , a = b = 1; ab/2 = 8; a = 4; -4.
a = -4 не подходит по условию задачи.
Итого: или х + у – 4 = 0.
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Уравнение прямой имеет вид: , где х1 = у1 = 0; x2 = -2; y2 = -3.
6.Расстояние от точки до прямой
Доказательство.
Пусть точка М1(х1,
у1)
– основание перпендикуляра, опущенного
из точки М на заданную прямую. Тогда
расстояние между точками М и М1:
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0, то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
Теорема доказана. |
Или Расстояние от точки до прямой
Длина
перпендикуляра, опущенного из данной
точки на прямую, называется расстоянием
от дочки до прямой.
Теорема.
Расстояние от любых двух точек
прямой до параллельной прямой равны.
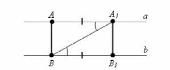 Пусть
а и b – параллельные прямые и точки A и
A1 – некоторые точки на прямой a. Опустим
из точки A перпендикуляр AB на прямую b и
отложим из точки B отрезок BB1, равный AA1
так, что бы A и B1 были по разные стороны
от прямой A1B.
Δ A1AB = Δ BB1A1 по первому
признаку равенства треугольников (A1B –
общая, ∠
AA1B = ∠
B1BA1 – как внутренние накрест лежащие,
AA1=B1B).
Из равенства треугольников
следует, что A1B1 тоже перпендикуляр к
прямой b и AB = A1B1. Теорема доказана.
Расстоянием
между параллельными прямыми
называется расстояние от какой-
Пусть
а и b – параллельные прямые и точки A и
A1 – некоторые точки на прямой a. Опустим
из точки A перпендикуляр AB на прямую b и
отложим из точки B отрезок BB1, равный AA1
так, что бы A и B1 были по разные стороны
от прямой A1B.
Δ A1AB = Δ BB1A1 по первому
признаку равенства треугольников (A1B –
общая, ∠
AA1B = ∠
B1BA1 – как внутренние накрест лежащие,
AA1=B1B).
Из равенства треугольников
следует, что A1B1 тоже перпендикуляр к
прямой b и AB = A1B1. Теорема доказана.
Расстоянием
между параллельными прямыми
называется расстояние от какой-
Биссектриса (от лат. bi- «двойное», и sectio «разрезание») угла — луч с началом в вершине угла, делящий угол на два равных угла[1]. Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.
В треугольнике под биссектрисой угла может также пониматься отрезок биссектрисы этого угла до её пересечения со противолежащей стороной треугольника.
Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).
Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно,[2] причём даже при наличии трисектора.[3]
Длина биссектрис в треугольнике
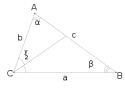

Биссектриса Треугольника ABC
Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.

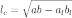
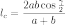
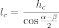
где:
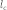 —
длина биссектрисы,
проведённой к стороне
—
длина биссектрисы,
проведённой к стороне
 ,
,
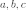 —
стороны треугольника
против вершин
—
стороны треугольника
против вершин
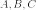 соответственно,
соответственно,
 —
полупериметр
треугольника,
—
полупериметр
треугольника,
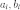 —
длины отрезков,
на которые биссектриса
делит
сторону
,
—
длины отрезков,
на которые биссектриса
делит
сторону
,
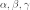 —
внутренние углы
треугольника при вершинах
соответственно,
—
внутренние углы
треугольника при вершинах
соответственно,
— высота треугольника, опущенная на сторону .

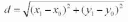 (1)
(1)