
- •1.Система координат
- •4.Уравнение прямой, проходящей через две заданные точки
- •5. Нормальное уравнение прямой
- •6.Расстояние от точки до прямой
- •7.Векторы
- •8.Общее уравнение плоскости в r3
- •10.Эллипс
- •11. Гипербола
- •Уравнения
- •Свойства
- •13.«Недекартовые» системы координат в пространстве
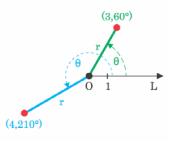
- •Полярные координаты
- •14.Сферическая система координат
- •15.Линейное пространство
- •Линейное векторное пространство. Линейное пространство векторов.
- •16.Линейная независимость
- •Определение
- •Свойства
- •Значение
- •17.Базис
- •Происхождение термина
- •Элементарное введение: базис в евклидовой плоскости и пространстве
- •Обозначения
- •Евклидово пространство
- •18.Ортогональность векторов. Перпендикулярность векторов.
- •19.Разложение вектора по базису
1.Система координат
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
3.Уравнение прямой в отрезках
Если
в общем уравнении прямой
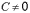 ,
то разделив (1) на
,
то разделив (1) на
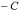 ,
получаем уравнение прямой в отрезках
,
получаем уравнение прямой в отрезках
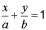 ,
,
где
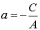 ,
,
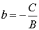 .
Прямая пересекает ось
.
Прямая пересекает ось
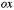 в точке
в точке
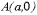 ,
ось
,
ось
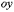 в точке
в точке
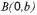 .
.
Пример
3. Дано общее
уравнение прямой
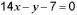 .
Записать данное уравнение прямой в
отрезках.
.
Записать данное уравнение прямой в
отрезках.
Решение.
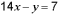 ,
разделим на 7, запишем
,
разделим на 7, запишем
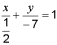 .
Это уравнение в отрезках. Оно говорит
о том, что данная прямая проходит через
точки
.
Это уравнение в отрезках. Оно говорит
о том, что данная прямая проходит через
точки
 ,
,
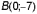 ,
т. е. Отсекает на положительной части
оси абсцисс
,
т. е. Отсекает на положительной части
оси абсцисс
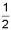 ,
на отрицательной части оси ординат –
(-7).
,
на отрицательной части оси ординат –
(-7).
Пример
4. Составить
уравнение прямой, отсекающей на осях
координат отрезки
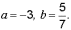
Решение.
Уравнение искомой прямой можно записать
в отрезках
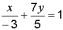 .
.
Легко
можно привести уравнение к общему виду
 .
.
Ответ:
 .
.
Уравнение прямой линии с угловым коэффициентом
Запишем уравнение прямой линии, пересекающей ось ординат в точке А(0, b), и образующей с осью абсцисс угол .
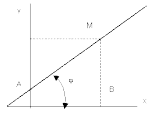
Выберем произвольную точку M(x; y) на прямой. Из Δ ABC имеем
 .
.
Откуда далее
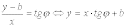 .
.
Если ввести обозначение углового коэффициента прямой
k = tg φ,
получим окончательно уравнение прямой с угловым коэффициентом
y = k·x + b.
З а м е ч а н и е. Этим уравнением нельзя пользоваться, если прямая перпендикулярна оси абсцисс, так как в этом случае угловой коэффициент такой прямой не определён.
4.Уравнение прямой, проходящей через две заданные точки
Выведем уравнение прямой линии, проходящей через две заданные точки M(x0, y0), M1(x1, y1).
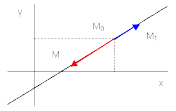
Для
этого выберем на прямой произвольную
точку М(x,
y).
Векторы
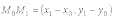 и
и
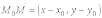 будут
коллинеарными. Признаком коллинеарности
векторов является пропорциональность
их соответствующих координат
будут
коллинеарными. Признаком коллинеарности
векторов является пропорциональность
их соответствующих координат
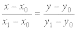 .
.
Это и есть искомое уравнение прямой, проходящей через две заданные точки.
Пучки
используются для установления отношений
между локальными и глобальными данными.
По этой причине они играют значительную
роль в топологии,
дифференциальной
геометрии и алгебраической
геометрии, но также применяются в
теории
чисел, анализе
и теории
категорий. Грубо говоря, пучок
 на
топологическом
пространстве
на
топологическом
пространстве
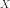 задаётся
данными двух типов с двумя дополнительными
свойствами.
задаётся
данными двух типов с двумя дополнительными
свойствами.
Первая
часть данных заключена в отображении,
сопоставляющем каждому открытому
подмножеству
 пространства
некоего
(абстрактного) множества
пространства
некоего
(абстрактного) множества
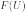 .
Можно требовать вдобавок, чтобы на этом
множестве была бы задана определённая
структура, но пока что ограничимся лишь
тем, что это просто множество.
.
Можно требовать вдобавок, чтобы на этом
множестве была бы задана определённая
структура, но пока что ограничимся лишь
тем, что это просто множество.
Вторая
часть данных состоит в том, что для
каждой пары открытых множеств
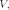
 первое
из которых вложено
во второе
первое
из которых вложено
во второе
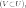 зафиксировано
некоторое отображение
зафиксировано
некоторое отображение
 ,
называемое отображением
ограничения.
(Оно действует аналогично операции
ограничения на область
,
называемое отображением
ограничения.
(Оно действует аналогично операции
ограничения на область
 функций,
заданных на
функций,
заданных на
 )
)
Требуется также, чтобы эти данные обладали следующими двумя свойствами:
Аксиома
нормализации:
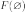 —
множество из единственного элемента.
—
множество из единственного элемента.
Аксиома
склейки:
если задана согласованная система
элементов
 (согласованность
означает, что элементы
(согласованность
означает, что элементы
 и
и
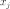 имеют
одно и то же ограничение на область
имеют
одно и то же ограничение на область
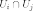 ),
то они однозначно определяют элемент
),
то они однозначно определяют элемент
 из
(где
—
объединение всех
из
(где
—
объединение всех
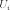 ),
ограничениями которого на соответствующую
область все они являются.
),
ограничениями которого на соответствующую
область все они являются.
