
- •21. Матрицы. Слу в матричной форме.
- •22. Матрица как линейный оператор
- •23. Умножение матриц.
- •24. Определители. Определители 2 и 3 –го порядков.
- •25. Свойства определителей.
- •26. Миноры. Алг. Дополнения
- •27. Разложение определителей по элементам строки.
- •28. Единичная матрица. Обратная матрица.
- •29. Теорема и формулы Крамера.
- •30. Решение линейных систем с помощью обратной матрицы
- •31. Метод Гаусса для решения линейных систем.
- •32. Решение слу методом Жордана-Гаусса
- •33. Ранг. Теорема Кронекера-Капелли
- •34. Собственные вектора и собственные значения.
- •35. Комплексные числа. Алгебра к.Ч.
- •36. Тригонометрическая форма к.Ч.
- •37. Формулы Эйлера. Показательная форма к.Ч.
- •38. Возведение в степень к.Ч.
- •39. Решение алгебраического уравнения n-ной степени. Извлечение корней к.Ч.
- •40. Логарифм к.Ч. (последняя формула)
21. Матрицы. Слу в матричной форме.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Матрицы допускают следующие алгебраические операции:
сложение матриц, имеющих один и тот же размер;
умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую строк);
умножение матрицы на элемент основного кольца или поля (т. е. скаляр).
Матричная форма
Система линейных уравнений может быть представлена в матричной форме как:
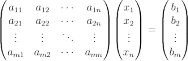 или:
или:
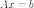
Здесь  —
это матрица системы,
—
это матрица системы,  —
столбец неизвестных, а
—
столбец неизвестных, а  —
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
—
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
22. Матрица как линейный оператор
Пусть
линейный оператор
действует
в сепарабельном гильбертовом пространстве.
Каждый элемент пространства может быть
представлен в координатах в некотором
ортонормированном базисе {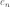 }
как
}
как 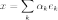 ,
причем из ортнонормированности базиса
следует, что
,
причем из ортнонормированности базиса
следует, что 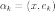 .
Тогда вектор
.
Тогда вектор 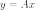 можно
разложить в том же базисе с коэффициентами
можно
разложить в том же базисе с коэффициентами  ,
где
,
где  .
Таким образом, в координатном
представлении
.
Таким образом, в координатном
представлении 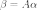 ,
где
,
где  -
координатное представление вектора
,
а
-
координатное представление вектора
,
а 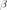 -координатное
представление вектора
-координатное
представление вектора  ,
соответственно
,
соответственно  {
{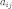 }-матрица
оператора в данном базисе.
}-матрица
оператора в данном базисе.
Таким образом, каждому линейному оператору гильбертова пространства соответствует некоторая матрица в данном базисе.
23. Умножение матриц.
Пусть
даны две прямоугольные
матрицы
и  размерности
размерности 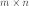 и
и 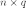 соответственно:
соответственно:
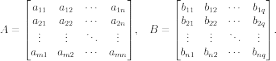
Тогда
матрица  размерностью
размерностью 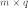 называется
их произведением:
называется
их произведением:

где:
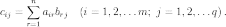
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Следует
заметить, что из существования
произведения 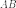 вовсе
не следует существование произведения
вовсе
не следует существование произведения 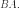
24. Определители. Определители 2 и 3 –го порядков.
Определителем
матрицы называется некоторая математическая
функция элементов квадратной матрицы,
результатом которой является
число.
Обозначение:
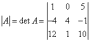 –
определитель 3- го порядка (т.к. матрица
размера 3 на 3) матрицы А.
Замечание:
В этом, якобы простом, определении
определителя ( звучит как тавтология)
говориться, что с элементами матрицы
нужно что то сделать ( умножить, сложить,
разделить и т.д.) и получится значение
определителя этой матрицы. Однако не
сказано. Что же все-таки надо с ними
сделать.
–
определитель 3- го порядка (т.к. матрица
размера 3 на 3) матрицы А.
Замечание:
В этом, якобы простом, определении
определителя ( звучит как тавтология)
говориться, что с элементами матрицы
нужно что то сделать ( умножить, сложить,
разделить и т.д.) и получится значение
определителя этой матрицы. Однако не
сказано. Что же все-таки надо с ними
сделать.
Вычисление
определителей первого порядка.
Матрица
размера  это
просто число. Определителем такой
матрицы является само это число.
Пример:
это
просто число. Определителем такой
матрицы является само это число.
Пример:
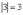
Вычисление
определителей второго порядка.
Определитель
второго порядка (матрицы размера 2 на
2) вычисляется по правилу:
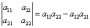 Запомнить
просто: произведение элементов, стоящих
на главной диагонали, минус произведение
элементов, стоящих на побочной.
Пример:
Запомнить
просто: произведение элементов, стоящих
на главной диагонали, минус произведение
элементов, стоящих на побочной.
Пример:
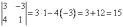 .
.
Вычисление
определителей третьего порядка.
Определитель
третьего порядка вычисляется по
правилу:
 Запомнить
порядок сомножителей, конечно же, очень
трудно, если не знать визуального
представления этого правила, которое
называется правило треугольников:
Запомнить
порядок сомножителей, конечно же, очень
трудно, если не знать визуального
представления этого правила, которое
называется правило треугольников:
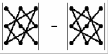 Здесь
схематично показано, какие сомножители
соседствуют в слагаемых.
Здесь
схематично показано, какие сомножители
соседствуют в слагаемых.
