25. Свойства определителей.

• Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):   , где   и т. д. — строчки матрицы,   — определитель такой матрицы.

• При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

• Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

• Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

• Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).

• С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

26. Миноры. Алг. Дополнения

Рассмотрим матрицу A:

  

Вычеркнем из матрицы k строк с номерами i₁, i₂, ..., i_k и k столбцов, с номерами j₁, j₂, ..., j_k.

Элементы, расположенные на пересечении вычеркнутых строк, образуют определиитель,

который называется минором порядка k. Его обозначают M_k:

Минор, образованный оставшимися элементами называется дополнительным минором

минора M_k и обозначают M_k'.

Алгебраическим дополнением A_k минора M_k называется число, равное дополнительному

минору M_k', умноженному на (−1) в степени, равной сумме номеров вычеркнутыж строк и

столбцов:

Если вычеркнуты одна строка и один столбец, то соответствующие миноры и алгебраические

дополнения называют минорами и алгебраическими дополнениями элемента.

Определитель равен сумме произведений элементов любой строки или любого столбца на их

алгебраические дополнения:

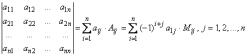
Минор, расположенный в первых k строках и k столбцах, называется угловым минором.

27. Разложение определителей по элементам строки.

 Рассмотрим квадратную матрицу  A  n-го порядка.        Выберем  i,j-ый элемент этой матрицы и вычеркнем  i-ую строку и  j-ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом  M_i j:

.

      Алгебраическое дополнение  A_i,j  элемента  a_i j определяется формулой

.

Теорема о разложении определителя по элементам строки. Определитель матрицы  A  равен сумме произведений элементов строки на их алгебраические дополнения:

.

28. Единичная матрица. Обратная матрица.

Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.

Определение

Квадратная матриц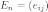а   размера (порядка  ), где 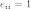  для всякого  , и   для всяких  , называется единичной матрицей порядка  .

Единичную матрицу можно определить как матрицу  , у которой  , где   - символ Кронекера.

Единичная матрица является частным случаем скалярной матрицы.

Обозначение

Единичная матрица размера   обычно обозначается   и имеет вид:

Так же используется и другое обозначение:  .

Если из контекста ясно, какого размера матрица, то нижний индекс (указывающий порядок) опускается:  ,  .

Свойства

• Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице:

• Квадратная матрица в нулевой степени дает единичную матрицу того же размера:

• При умножении матрицы на обратную ей тоже получается единичная матрица:

• Единичная матрица получается при умножении ортогональной матрицы на её транспонированную матрицу:

• Определитель единичной матрицы равен единице:

.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы

• , где   обозначает определитель.

•  для любых двух обратимых матриц   и  .

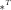•  где   обозначает транспонированную матрицу.

•  для любого коэффициента   .

• Если необходимо решить систему линейных уравнений  , (b — ненулевой вектор) где   — искомый вектор, и если   существует, то  . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.