29. Теорема и формулы Крамера.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Описание метода

Для системы   линейных уравнений с   неизвестными (над произвольным полем)

с определителем матрицы системы  , отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что   отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы   и  , либо набор 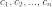  состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

30. Решение линейных систем с помощью обратной матрицы

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с   неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:

, где   — основная матрица системы,   и   — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на   — матрицу, обратную к матрице  : 

Так как  , получаем  . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулюопределителя матрицы A:

.

Для однородной системы линейных уравнений, то есть когда вектор  , действительно обратное правило: система   имеет нетривиальное (то есть ненулевое) решение только если  . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

31. Метод Гаусса для решения линейных систем.

Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме.Для того чтобы решить систему уравнений

  выписывают расширенную матрицу этой системы  и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы   будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы.