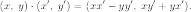34. Собственные вектора и собственные значения.

   Собственные векторы и собственные значения линейного оператора 

     Ненулевой вектор   называется собственным вектором линейного оператора 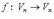 , если   (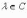  для комплексного  ), такое, что   Число   называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.

     Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор   имеет координатный столбец X, то   или 

     Собственные числа   линейного оператора   - корни характеристического уравнения  , где   - матрица оператора f,   - символ Кронекера.

     Для каждого собственного значения   соответствующие собственные векторы могут быть найдены из матричного уравнения   или соответствующей ему системы линейных уравнений

     Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид

где   - соответствующие собственные значения.

35. Комплексные числа. Алгебра к.Ч.

Ко́мпле́ксные чи́сла (устар. Мнимые числа), — расширение множества вещественных чисел, обычно обозначается  . Любое комплексное число может быть представлено как формальная сумма  , где   и   — вещественные числа,   — мнимая единица.

Комплексное число   можно определить как упорядоченную пару вещественных чисел  . Введём операции сложения и умножения таких пар следующим образом:

• 

• 

Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида  , причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой  единица —   а мнимая единица —   На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен  , то есть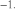 

Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно.

Действия над комплексными числами

• Сравнение

 означает, что   и   (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

• Сложение

• Вычитание

• Умножение

• Деление

36. Тригонометрическая форма к.Ч.

Обозначим к.ч. в качестве радиус-вектора на комплексной плоскости (рис. 13.1). Определим как модуль к.ч., угол между осью  и радиус-вектором , отсчитывание которого осуществляется в положительном направлении.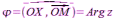 назовем аргументом к.ч. Понятно, что находится неоднозначно. Основным значением будем именовать , который удовлетворяет неравенствам или В этом случае

Заметим, что для аргумент не определен. Из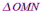 (рис. 13.1) получаем:

 

(13.1)

 

т.е. имеет вид

Подобная форма записи определяется как тригонометрическая форма к.ч.

Осуществляя переход от алгебраической к тригонометрической форме применим формулы (13.1) и соотношения

 

Пример: обозначить в тригонометрической форме.