3 . Характеристики вращательного движения тела при его плоском движении не зависят от выбора полюса.

Доказательство

Пусть положение подвижной системы координат определяет система

   осей   Bx₁y₁    и    уравнения     X_B  = X_B (t)   ;   Y_B = Y_B(t)  ;   ₁  = ₁(t) .  

       Покажем на чертеже прежнюю систему координатных осей с полюсом   в  точке А;   перенесем эти оси параллельно самим себе в точку В и обозначим угол между новой осью Вx₁  и  старой осью  Аx через  .  

 Так как обе системы координат связаны с точками твердого тела,  то   угол    при движении тела  остается постоянным  и  в любой момент времени выполняется равенство

 ₁  =    +  .

         Дифференцируя по времени уравнение вращательного движения подвижной системы координат,  получим :

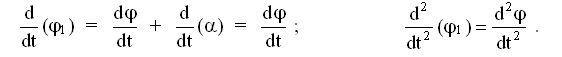
 Теорема доказана.

За полюс можно принимать любую точку тела.  Это утверждение окажется очень полезным для решения всех задач, связанных с определением скоростей  и  ускорений  точек  тел  при  их  плоском  движении.

Формулировки  теорем,  с помощью которых определяются скорости и ускорения точек тел при их плоском движении, аналогичны.     Поэтому сформулируем  и докажем  эти теоремы одну за другой. 

   Скорость  любой  точки  тела  при  плоском  движении  равна геометрической  сумме  скорости  полюса  и  скорости  во  вращении   точки  относительно  полюса.

             Ускорение   любой  точки  тела  при  плоском  движении  равно геометрической  сумме  ускорения  полюса и  ускорения  во  вращении точки  относительно  полюса.

  В записи эти теоремы имеют следующий  вид:

 =  +  =   +   ;

  =   +  =    +  .

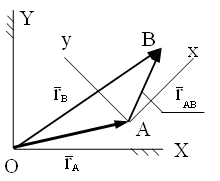
                          Для доказательства теорем определим положение точек  А  и В  относительно  неподвижной системы  отсчета радиусами-векторами    и  ,  а  точки  сечения  соединим вектором .

В любой момент движения сечения  является справедливым  векторное равенство       =   +  .

Продифференцируем это векторное равенство по времени:

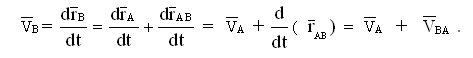
При  постоянстве модуля вектора  производная по времени от этого вектора во вращающейся вместе с телом системе координатных осей равна скорости вращения конца вектора  (т. В) относительно точки А.      

Обозначать эту скорость принято символом  . Определяется эта скорость векторным произведением вектора угловой скорости вращения  координатных осей  и  вектора, соединяющего точку В  с полюсом .

          Вектор угловой скорости  тела  при  его плоском  движении  перпендикулярен  плоскости,  в  которой  движется  сечение  тела.       На  чертеже  этот  вектор  не  изображают.

         Первая теорема доказана.  Для  доказательства теоремы об ускорениях точек  продифференцируем  по  времени  теорему  о  сложении  скоростей.

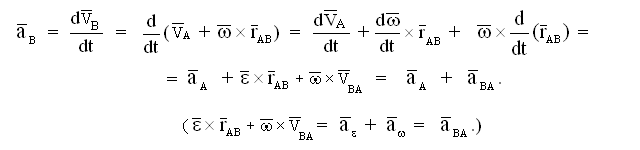
          Так как геометрическая сумма вращательного и осестремительного ускорений определяет полное ускорение т. В   в  ее вращении относительно полюса,  можно считать доказанной  и  вторую теорему.  Остается теперь внимательно разобраться с каждым из полученных векторных равенств и подумать об эффективном  применении этих равенств и следствий из них при решении задач.

     Начнем с теоремы о сложении скоростей  (плакак 13к)

  Возьмем и построим векторное  равенство  = + , связывающее скорость точки В произвольного отрезка АВ со скоростью полюса при плоском движении фигуры .

        Для определения скорости т. В  вектор скорости полюса  -    перенесем  параллельно  самому себе  в т. В и сложим по правилу  векторного параллелограмма с вектором скорости  во вращении   т. В  относительно полюса.   

     Вектор  определим по величине угловой скорости

                                         вращения фигуры и  расстоянию от  т. В  до полюса   (  ).      

  Направлен  перпендикулярно АВ.

  Из  теоремы   можно  получить несколько  очень полезных  для решения задач следствий.

                  Следствие 1.   Проекции скоростей точек тела при его плоском движении на прямую, соединяющую точки,  равны.

 Добавим, что следствие о равенстве проекций скоростей точек тел  на  соединяющую  их  прямую

справедливо и при любых других видах движения твердых тел.

  Следствие 2.  Разность проекций скоростей точек прямолинейного отрезка АВ на перпендикуляр к  АВ   равна скорости во вращении одной точки относительно другой.

          Из   V_By  = V_Ay   +  V_BA   получаем    V_By  - V_Ay   =  V_BA      и  ...  удобную формулу для определения угловой скорости фигуры при ее плоском движении по скоростям двух ее точек.

.

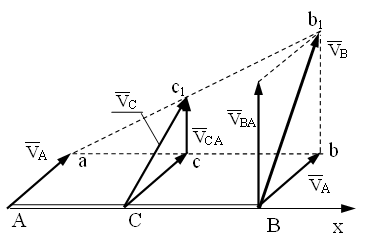
         Следствие 3.   Концы векторов скоростей точек прямолинейного отрезка  лежат на одной прямой  и делят отрезок между концами векторов скоростей крайних точек на части в том же отношении, в каком точки делят сам отрезок.

          Для доказательства этого положения соединим концы векторов скоростей   точек  А и В  отрезком   аb₁   и определим скорость еще одной точки отрезка - вектор скорости точки  С.

 В соответствии с теоремой      =     +   .

       Для  всех точек отрезка  АВ  скорость полюса одинакова  и  равна  .

Концы  векторов скорости полюса для всех точек отрезка лежат на прямой ab,  параллельной АВ.

 

         Вращательные скорости точек относительно полюса пропорциональны  их расстояниям до полюса.  В треугольнике аbb₁ с высотой, равной вектору ,  концы векторов вращательных  скоростей  вследствие  их пропорциональности  расстояниям от точки а  лежат на гипотенузе  треугольника  -  линии  ab₁.  На этой же прямой после сложения векторов  и будет находиться и конец вектора скорости точки С.        А  из подобия треугольников   асс₁  и  аbb₁  следует, что                      

.

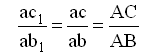Следствие 4.   В любой момент непоступательного движения плоской фигуры  на плоскости,  связанной с фигурой, существует точка, скорость которой равна нулю.

         Точку  эту называют мгновенным центром скоростей ( принятое сокращение - М.Ц.С. ) и обозначают, как правило, буквой  Р.

         Доказательство следующее.   Векторы  скоростей  точек плоскости, связанной с фигурой, определяются  векторной  суммой двух векторов, один из которых одинаков для всех точек  плоскости, а другой зависит от положения точки на плоскости.  Значит, на плоскости должна существовать точка,  где вектор скорости во вращении относительно полюса равен по  величине,  но  направлен противоположно вектору  скорости  полюса.  Эта точка и будет иметь скорость, равную нулю,  т.е. являться  мгновенным центром скоростей.

 

       Вектор скорости точки  В  равен по модулю произведению угловой скорости вращения фигуры на ее расстояние до мгновенного центра скоростей.   Направлен вектор скорости  т.  В  перпендикулярно отрезку,  соединяющему точку с М.Ц.С.

        Аналогично можно определить величину и направление скорости любой другой точки фигуры и   ... сделать  следующие  выводы :

           1.   При выборе в качестве полюса мгновенного центра скоростей величины и направления скоростей точек тела при его плоском движении определяются точно так же,  как и при вращательном.  Отличием является то,  что для каждого момента движения тела положение мгновенной оси вращения необходимо находить.   Соответственно необходимо находить и расстояния точек до этой оси.

          2.   Скорости всех точек фигуры при ее плоском движении пропорциональны их расстояниям до М.Ц.С.  и перпендикулярны  радиусам  вращения  -  т.е.  отрезкам, соединяющим точки с М.Ц.С.

          3.   Если уметь определять положение мгновенных центров скоростей звеньев  плоских  механизмов,  то  задачи  на  определение  скоростей  точек  и угловых скоростей звеньев  этих механизмов окажутся ничуть не сложнее аналогичных задач на вращательное движение связанных между собой тел.

             Все типовые случаи определения положения М.Ц.С. известны. В этом отношении случай, рассмотренный на рисунке выше, не является типичным.     Угловые скорости звеньев плоских механизмов в задачах  обычно являются искомыми величинами.    И определяются они,  как правило,  по известной скорости одной  из точек фигуры  и ее расстоянию до  М.Ц.С.

К типовым  же случаям определения   М.Ц.С.  относят следующие:

 

1.   Качение колеса без скольжения по неподвижной поверхности.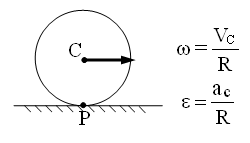

        

          В каждый момент движения тела  при его качении без скольжения 

                М.Ц.С. -  это точка  касания тела и неподвижной поверхности.

    Угловая скорость колеса определяется из  отношения  скорости  центра  колеса  к  его  радиусу.

 

2.   Случай,  когда  известны  направления  движения  двух  точек тела,   

и  эти  направления  н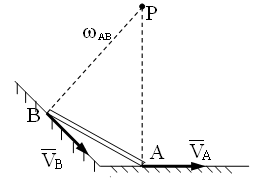 е  параллельны.

         М.Ц.С.  находится на пересечении перпендикуляров к векторам скоростей точек.   В этом случае по известной скорости одной из точек и ее расстоянию до М.Ц.С.  сначала определяют угловую скорость  и направление вращения фигуры,  а затем определяют величину скорости другой точки и направление вектора скорости.

 

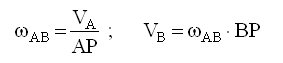
3. Случай, когда векторы скоростей точек параллельны между собой

и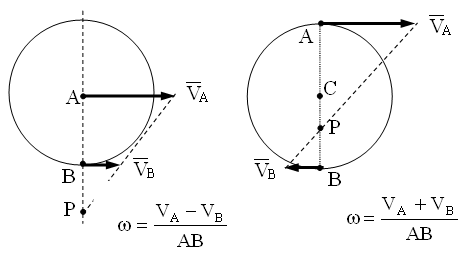 перпендикулярны  отрезку,  соединяющему  точки.    

        Этот случай часто встречается,  когда определяются  угловые скорости тел качения 

 

     М.Ц.С.   находится на пересечении  линии,  соединяющей точки,  и линии,  соединяющей концы векторов скоростей точек.  Величины скоростей точек в этом случае должны быть известны.

 

         При противоположном направлении  векторов скоростей  М.Ц.С.  расположен между точками, скорости которых известны; при одинаковом направлении -  со стороны меньшей скорости и на продолжении отрезка,  соединяющего точки.

      Угловые скорости тел в этом случае по скоростям  двух точек могут определяться  сразу (следствие 2) по формулам,  приведенным  рядом  с  рисунками.   Находить  расстояния точек   до   М.Ц.С.  в этом случае,  если  это не требуется для определения скоростей каких-либо других точек,  необязательно.

        4. Случай, когда векторы скоростей точек параллельны между собой и не перпендикулярны отрезку, соединяющему  точки. 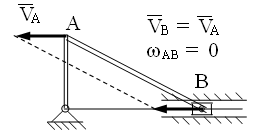                                           В этом случае принято говорить о мгновенно поступательном движении тела.  А  это значит, что в данный момент движения фигуры  (звена АВ).

1)  угловая  скорость  тела равна нулю;

     2)  М.Ц.С. находится в бесконечности ;

     3)  скорости всех точек тела равны между собой.

    Следует добавить также, что равенство скоростей наблюдается только в данный момент движения тела.     Ускорения точек тела различны.

           Рассмотрим  таким же образом  ( плакат 14к ) теорему о сложении ускорений точек в  плоском  движении  и  построим  на рисунке  векторное  равенство 

   =  + .

    В соответствии с теоремой для определения ускорения точки  В  по ускорению полюса  А  необходимо:

1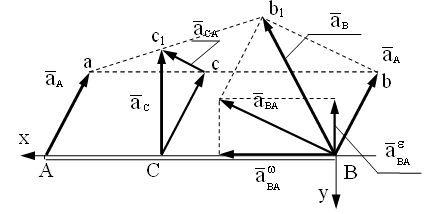 ) вектор ускорения полюса    перенести в точку В ;

 

 2)  рассчитать по величине и построить на чертеже в том же масштабе векторы и ,  а затем и полное ускорение   ; 

3)  сложить  в  т. В   векторы   и  либо по правилу векторного параллелограмма,  либо по правилу векторного многоугольника.

          Из  рисунка видно,  что построение этого векторного равенства немногим отличается от построения предыдущего.  Только вектор  был  перпендикулярен   АВ, а вектор   образует с АB  угол , зависящий от угловой скорости  и  углового ускорения фигуры.

         1.   Концы векторов ускорений точек прямолинейного отрезка лежат на прямой, соединяющей концы векторов ускорений крайних точек,  и  делят отрезок  прямой  на части в том же отношении, в каком  точки делят сам отрезок .

         Доказывается это абсолютно так же, как следствие из предыдущей теоремы.   Достаточно посмотреть на рисунок  и определить ускорение какой-либо еще точки отрезка АВ.

         2.   В любой момент движения плоской фигуры (за исключением случая ее поступательного движения) на плоскости, связанной с фигурой,  существует точка, ускорение которой равно нулю.  Точку  эту называют мгновенным центром ускорений  (принятое сокращение - М.Ц.У.)   и обозначают на чертеже,  как правило,  буквой  Q.

                   И это положение  доказывается точно так же,  как  и положение о существовании  М.Ц.С. .

         Найдем  на  рисунке  положение  М.Ц.У.  по ускорению полюса и характеристикам вращательного движения фигуры - угловой скорости и угловому  ускорению.

         Определив  таким  образом  ускорения  нескольких  точек  фигуры,  из теоремы  об  ускорениях  точек  тел  при их плоском движении  также можно  сделать  определенные  выводы.

         1.   Ускорения точек  тела  при  его плоском  движении  в  каждый  момент  движения  распределены так,  как будто тело вращается относительно оси,  проходящей через мгновенный центр  ускорений.

       2.   Ускорения всех точек тела пропорциональны их расстояниям до   М.Ц.У.  и образуют с отрезками,  соединяющими точки с М.Ц.У.,  равные  углы  μ.

             Полезные для решения задач выводы можно сделать и  из проекций векторного равенства 

     =  +      на  координатные оси,  направленные вдоль  АВ  и  перпендикулярно к  АВ.    Их  мы рассмотрим  позже  -   при обсуждении  задач  в  главе  2.

           И, наконец,  мгновенный центр ускорений  не  совпадает с мгновенным центром скоростей .    М.Ц.С.   и  М.Ц.У.   -   это  разные  точки  плоскости.

При    V_P  =  0    a_р    0;     при    a_Q  =  0     V_Q    0.