Относительным называют движение точки, рассматриваемое по отношению к подвижной системе отсчета .
То есть движение точки по некоторому телу, которое само перемещается каким-либо образом относительно вводимой для решения задачи неподвижной системы отсчета.
В движении по телу рассматриваемая точка может перемещаться либо по прямой, либо по кривой. Эту траекторию (мы будем называть ее относительной) видит наблюдатель, физически (или в большинстве задач мысленно) связанный с движущимся телом. То есть, наблюдатель, как бы находящийся в подвижной системе координат.
Скорость и ускорение точки при ее движении по телу (т.е. относительно подвижной системы отсчета) называют относительной скоростью и относительным ускорением и обозначают символами Vr и ar c индексом r.
(Индекс в данном случае от слова “relative”. Вспомните его перевод.)
Абсолютным называют движение точки относительно неподвижной системы отсчета.
Это движение видит наблюдатель, находящийся в неподвижной системе отсчета. Траектория точки здесь называется абсолютной, а скорость и ускорение точки относительно неподвижной системы отсчета называют абсолютной скоростью и абсолютным ускорением точки. Их принято обозначать символами Va и aa с индексом а.
Переносным для точки, совершающей сложное движение, называют движение подвижной системы отсчета ( и всех связанных с ней точек ) относительно неподвижной системы отсчета.
Неподвижный наблюдатель переносное движение видит, как движение тела, по которому перемещается совершающая сложное движение точка.
Скорости различных точек тела при его в общем случае непоступательном движении различны. Поэтому под переносной скоростью и переносным ускорением точки понимают скорость и ускорение той точки подвижной системы отсчета (то есть движущегося тела), где находится в данный момент точка, сложное движение которой рассматривается .
Переносную скорость и переносное ускорение точки принято обозначать символами Ve и ae с индексом - е . ( Индекс здесь от глагола “entreinen” - т.е. увлекать с собой.)
При изучении сложного движения точки в кинематике доказываются две теоремы: теорема об определении абсолютной скорости точки и теорема об определении ее абсолютного ускорения. Последняя для случая произвольного переносного движения была доказана французским математиком и механиком Кориолисом и с тех пор носит его имя. Мы докажем эти теоремы одну за другой. Предварительно сформулируем их.
Теорема 1. Абсолютная скорость точки в сложном движении равна векторной сумме ее относительной и переносной скоростей .
Теорема 2. ( теорема Кориолиса )
Абсолютное ускорение точки при непоступательном переносном движении равно векторной сумме трех ускорений - относительного, переносного и поворотного .
(Последнее называют ускорением Кориолиса и обозначают символом ас .)
В записи эти теоремы имеют вид :
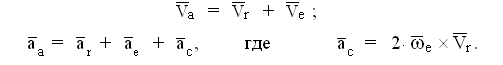
Примем его за основу и совместим для доказательства начало подвижной и неподвижной системы отсчета в одной точке.
При доказательстве рассмотрим сложное движение точки, которая движется по некоторой кривой на поверхности сферы , вращающейся относительно проходящей через начало неподвижной системы отсчета оси.
Как было сказано ранее, начало подвижной, связанной со сферой, системы координат, совместим с началом неподвижной системы отсчета.
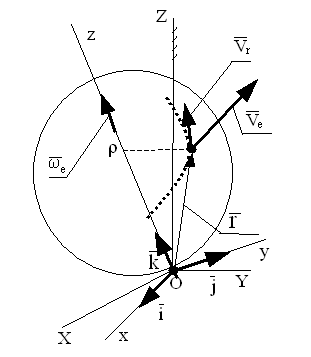
Орты подвижной системы координатных осей обозначим, как обычно, символами , и . Орт направим вдоль оси переносного вращения тела.
Вдоль
этой же оси направлен вектор угловой
скорости переносного вращения
-
.
Положение
точки относительно начала отсчета
определим радиус-вектором -
.
На основании введенных понятий движение точки по сфере будем рассматривать как ее относительное движение; вращение сферы для точки будем считать переносным движением. Движение точки относительно неподвижной системы координат будем рассматривать как абсолютное.
В относительном движении в подвижной системе отсчета будут изменяться только координаты точки - x, y и z.
При координатном способе задания движения скорость и ускорение точки мы уже определяли выражениями :
;
К рассмотренным ранее выражениям добавились только новые индексы в обозначениях величин V и a.
В переносном движении изменяются направления ортов и , связанных с вращающимся шаром координатных осей x и y. Эти орты вращаются вокруг оси Оz ( оси вращения шара ) с угловой скоростью переносного вращения.
Формулы для определения скорости и ускорения любой точки вращающегося тела, положение которой относительно оси вращения задано радиус-вектором, нам известны. Следовательно, по определению, переносная скорость и переносное ускорение точки должны определяться выражениями:
;
.
А теперь, учитывая то, что введенный нами радиус-вектор описывает движение точки не только относительно подвижной, но неподвижной системы отсчета, найдем абсолютную скорость и абсолютное ускорение точки по формулам:
В отличие от рассмотренного ранее случая дифференцируем выражение, определяющее радиус-вектор, как сумму произведений переменных величин. При преобразовании получаемых выражений вспомним формулы Пуассона.
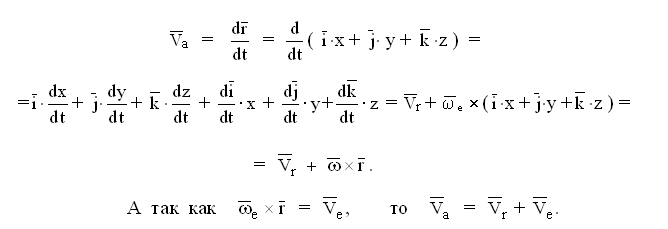
Следовательно, первая теорема доказана.
Для доказательства теоремы Кориолиса возьмем вторую производную от радиус-вектора движущейся точки.
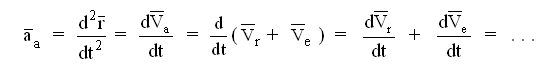
Только
для того, чтобы получаемое
выражение для определения абсолютного
ускорения не получалось слишком
громоздким, запишем определение
производных от
и
отдельно.
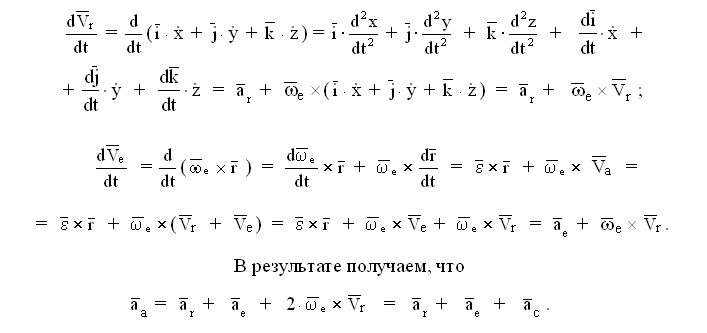
Итак, теорема доказана. В ходе доказательства получен любопытный результат. При дифференцировании по времени относительной и переносной скоростей кроме относительного и переносного ускорений нами были получены две совершенно одинаковые добавки. Их сумма и была названа поворотным (кориолисовым) ускорением.
Что же характеризует это ускорение ? Ответ на этот вопрос легко получить, рассмотрев совсем простой случай сложного движения точки, когда эта точка перемещается с постоянной по величине скоростью по радиусу равномерно вращающегося диска. Рассмотрим этот случай на рисунке ниже.
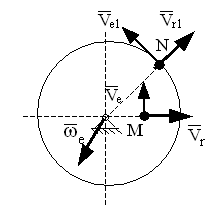
Пусть за некоторый промежуток времени диск повернется на некоторый
угол φ а точка переместится по радиусу из точки М в точку N.
Сравним
векторы
и
,
построенные в каждой из точек.
Мы увидим, что :
1. Вектор при повороте диска изменил свое направление.
2. Вектор кроме обычного при вращательном движении тела
изменения по направлению изменился и по величине.
Не будем доказывать, что рассматриваемые изменения одинаковы, а просто отметим, что кориолисово ускорение точки при непоступательном переносном движении характеризует изменение сразу двух скоростей - - относительной по направлению и переносной по величине .
Эти изменения - следствие вращения подвижной системы координат и перемещения точки относительно оси вращения.
Остается научиться только находить это новое для нас ускорение по величине и направлению; и рассмотреть все случаи, когда это ускорение равно нулю.
Модуль кориолисова ускорения находится, как модуль векторного произведения рассматриваемых векторов.
1) e = 0, т.е. когда подвижная система отсчета движется поступательно;
2) Vr = 0 - тривиальный случай;
3)
=
0 - когда точка движется
параллельно оси переносного вращения.
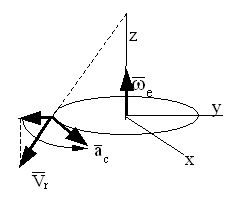
Для определения направления вектора кориолисова ускорения можно использовать правило, в соответствии с которым определяется направление вектора, являющегося векторным произведением двух векторов.
Но значительно проще и быстрее можно определять направление этого вектора с помощью правила Н. Е. Жуковского.
Для определения направления вектора кориолисова ускорения необходимо вектор относительной скорости точки спроектировать на плоскость, перпендикулярную оси переносного вращения, и повернуть проекцию вектора в этой плоскости по направлению вращения на 900.