Московский авиационный институт

(национальный исследовательский университет)

Курсовая работа

по математическому анализу

Вариант № 10

Выполнил: студент гр. 30-103 С

Поляков Александр Романович

Проверил:

Лебедев Максим Витальевич

Москва 2011/12 уч. год

Оглавление

Теория………………………………………………………………….3

Точки разрыва и их классификация……………………………………………………...3

Основные сведения. Тригонометрические ряды Фурье для функций с периодом 2π…………………….3

Тригонометрический ряд. Ряд Фурье……………………………………………………………………………4

Достаточные признаки разложимости функции в ряд Фурье………………………………………………….8

Ряды Фурье для четных и нечетных функций с периодом 2π…………………………………………………9

Тригонометрические ряды Фурье для функций любого периода…………………………………………..11

Ряд Фурье четной и нечетной функций любого периода Т (Т = 2l)………………………………...……12

Комплексная форма ряда Фурье………………………………………………………………………………12

Комплексная форма ряда Фурье периодической функции периода Т=2l…………………………………...14

Интеграл Фурье…………………………………………………………………………………………………….14

Интеграл Фурье для четной и нечетной функций……………………………………………………………..17

Интеграл Фурье в комплексной форме……………………………………………………………………...…18

Преобразование Фурье………………………………………………………………………………………….20

Теория.

Точки разрыва и их классификация.

Пусть функция ƒ(x) определена в некоторой окрестности точки x₀, кроме, быть может, самой точки x_0. Из приведенного ранее определения точки разрыва функции получаем, что точка x₀ является точкой разрыва функции ƒ(x), если выполняется одно из условий: или функция ƒ(x) определена в точке x₀, но не является непрерывной в этой точке, или функция ƒ(x) не определена в точке x₀.

В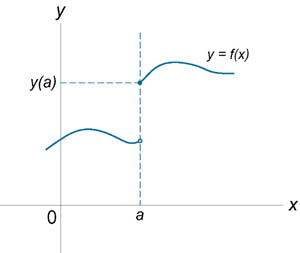 первом случае точка x₀ принадлежит области определения функции, во втором случае x₀ не принадлежит области определения функции. Заметим, что для основных элементарных функций возможен только второй случай.

П

Рис. 1

усть x₀ − точка разрыва функции ƒ(x). При этом x₀ называется точкой разрыва первого рода, если функция ƒ(x) имеет конечные пределы справа и слева в этой точке. Во всех остальных случаях х₀ называется точкой разрыва второго рода. Если x₀ − точка разрыва первого рода функции ƒ(x), то график этой функции в

точке x₀ может иметь лишь конечный скачок (см. рис. 1). Если же x₀ − точка разрыва второго рода функции ƒ(x), то, по крайней мере, один из пределов справа или слева в точке x₀ не существует или равен бесконечности.

Основные сведения. Тригонометрические ряды Фурье для функций с периодом.

Функция ƒ(x), определенная на всей числовой оси, кроме, быть может, изолированных точек, называется периодической, если существует такое число Т (Т≠0), что при любом значении х выполняется равенство

ƒ(х+Т)= ƒ(x) (1)

Ч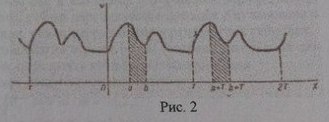 исло Т в этом случае называется периодом функции. Как следует из определения периодической функции, для построения графика такой функции достаточно построить ее график на отрезке [0, Т] и периодически продолжить его на всю числовую ось (рис. 2). (Прибавление числа к аргументу функции означает сдвиг графика этой функции вдоль оси ОХ.)

Из определения также следует, что если Т − период функции, то ее периодом также будет nT, где n − любое целое число. Обычно за период Т принимают наименьшее положительное число, удовлетворяющее равенству (1).

Отметим следующие свойства периодических функции:

1) Сумма, разность, произведение и частное периодических функций периода Т есть периодические функции периода Т.

2) Если функция ƒ(x) имеет период Т, то функция ƒ(ах) имеет период T/a

3) Если ƒ(x) − периодическая функция периода Т, то равны любые два интеграла от этой функции, взятые по промежуткам длины Т (при этом предполагается, что эти интегралы существуют), т.е. при любых а и b справедливо равенство

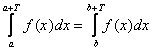
(геометрически для неотрицательных функций имеем равенство площадей, рис 2).

Действительно,

_{a + T h h + T a + T}

∫ ƒ(x)dx = ∫ ƒ(x)dx + ∫ ƒ(x)dx + ∫ ƒ(x)dx

^{a a b b + T}

Преобразуем теперь интеграл

_{a + T}

∫ ƒ(x)dx

^{b + T}

Полагая х=u+T:

_{a + T a a}

∫ ƒ(x)dx = ∫ ƒ(u + T)du ∫ ƒ(u)dx

^{b + T b b}

(при этом мы воспользовались периодичностью функции ƒ(u)). И окончательно получаем:

_{a + T b b + T a h + T}

∫ ƒ(x)dx = ∫ ƒ(x)dx + ∫ ƒ(x)dx + ∫ ƒ(x)dx= ∫ ƒ(x)dx

^{a a b b h}