17. Типы элементов, используемых в мкэ.
На практике используются три типа элементов: симплекс-элемент, комплекс-элемент и мультиплекс-элемент [17].
Симплекс - элементам соответствуют полиномы, содержащие константу и линейные члены. Одномерный симплекс-элемент аппроксимирует функцию линией: (х) = 1 +2 x. Полином, аппроксимирующий поведение функции в пределах треугольного симплекс-элемента, дается уравнением плоскости: (х) = 1 +2x+2y .
Комплекс–элементам соответствуют полиномиальные функции, содержащие константу, линейные члены, члены второго и более высоких порядков. Форма комплекс – элементов может быть такой же как у симплекс - элементов, но с дополнительными граничными или внутренними узлами. Интерполяционный полином для 2-мерного треугольного комплекс – элемента с шестью узлами имеет вид:
.
Для мультиплекс – элементов также используются полиномы, содержащие члены высокого порядка, Однако, для обеспечения непрерывности при переходе от одного мультиплекс – элемента к другому границы элементов должны быть параллельны осям координат.
Одномерный симплекс-элемент.
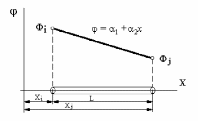
Одномерный симплекс – элемент представляет собой прямолинейный отрезок длины L с двумя узлами – по одному на каждом конце отрезка (рисунок 3.1.2). Узлы обозначаются индексами i и j, значения функции в узлах – через Фi и Фj соответственно.
|
Рис. 3.1.2 |
Начало системы координат располагается вне КЭ. Полиномиальная функция для скалярной величины (например, температуры – Т или давления – Р) такова:
= 1 +2 x
Коэффициенты 1 и 2 определяются с помощью условий в узловых точках:
= Фi при x = Xi и = Фj при x = Xj.
Эти узловые условия приводят к системе двух уравнений:
Фi = 1 +2 Xi; Фj = 1 +2
решение которой дает:
1= (Фi Xj - Фj Xi)/L; 2 = (Фj - Фi )/L
Подставляя найденные значения 1 и 2 в формулу (9.3), получим:
= (ФiXj-ФjXi)/L +{(Фj-Фi)/L}x
Данное уравнение может быть переписано в виде:
= [(Xj-x)/L]Фi+[(x-Xi)/L]Фj
Линейные функции от х в формуле называются функциями формы или интерполяционными функциями. Далее эти функции обозначаются через N. Каждая функция формы должна быть снабжена нижним индексом для обозначения узла, к которому она относится. Произвольную функцию формы будем обозначать через N. В формулу входят следующие функции формы:
-
Ni =
Xj-x
;
и
Nj =
x-Xi
L
L
Используя эти функции формы, запишем выражение (9.5) в матричной форме:
-
= NiФi + NjФj = [N]{Ф} = [Ni Nj]
Фi
= [Ni Nj] [Фi Фj]Т
Фj
Функция Ni = 1 в узле с номером i и равна нулю в j-м узле. Аналогично функция Nj = 1 в узле с номером j и равна нулю в i-м узле. Эти значения характерны для функций формы. Они равны 1 в одном определенном узле и обращаются в 0 в остальных узлах.
Пример 3.1.1. Одномерный симплекс-элемент используется для аппроксимации температуры в стержне. Узлы 1 и 2 имеют координаты 1,5 и 6 см соответственно. Известно, что температура в узлах 1 и 2 равна 120 и 90 градусов соответственно. Требуется определить температуру в точке х = 4 см и градиент температуры внутри элемента.
Решение: Пользуясь выражением (9.5) для одномерного симплекс – элемента, можно записать закон изменения температуры внутри КЭ:
-
t =
(Xj-x)
Ti +
(x-Xi)
Tj
L
L
Данные КЭ: Xi=1,5 см; Ti=120oC; X j=6,0 см;
Tj=90oC; x=4 см; L = (Xj – Xj ) = 4,5 см.
Подставляя данные в формулу для температуры получаем:
-
t =
(1,5 - 4)
120o +
(4 – 1,5)
90o = 103,33 oC
4,5
4,5
Для градиента температуры имеем:
-
dt
= -
Ti
+
Tj
= -
120o
+
90o
= -6,67 oC/см
dx
L
L
4,5
4,5