§2.4 Соединение звеньев и преобразование структурных схем

Математическая модель системы содержит в себе информацию о структуре и свойствах отдельных элементов САУ. Структурная схема, являясь графическим изображением математической модели, дает наглядное представление о звеньях, входящих в систему. Звено, как уже отмечалось, на структурной схеме условно обозначают в виде прямоугольника с указанием входных и выходных переменных, а также оператора внутри него. Если оператором является передаточная функция, полученная с использованием преобразования Лапласа, то входные и выходные переменные записывают в форме изображений. Если переменные рассматриваются как функции времени, то оператор определяется уравнением (системой уравнений), описывающим работу элемента (системы).

Наиболее удобным способом объединения математических моделей отдельных элементов с целью получения уравнения динамики или передаточных функций замкнутой системы в инженерной практике считается метод структурных преобразований, позволяющий с помощью ряда правил громоздкую структуру свести («свернуть») к простой, удобной для получения эквивалентных передаточных функций. Такое преобразование равносильно исключению промежуточных переменных в заданной математической модели.

Структурные преобразования предполагают, прежде всего, выделение и замену часто встречающихся типовых соединений звеньев эквивалентными передаточными функциями.

Типовые соединения звеньев. К типовым относят последовательное, параллельное и параллельное встречное (с обратной связью) соединения звеньев.

а ) х(р) х₁(р) у(р)

б) в)

y₁(p) y(p) e(p) y(p)

x(p) y(p)

y₁(p)

y₂(p)

Рис.2.15 Типовые соединения звеньев: последовательное (а), параллельное (б),

с отрицательной обратной связью (в)

При последовательном соединении звеньев выходная величина одного звена является входной величиной другого (рис.2.15,а). При получении эквивалентной передаточной функции соединения W(р) будем исходить из определения передаточной функции:

W₂(p)= или y(p)=W₂(p)x₁(p).

Заменяя x₁(p), окончательно получим

y(p)=W₁(p)W₂(p)x(p) или W(p)=W₁(p)W₂(p).

Если последовательно соединено звеньев, то

W(p)= (2.12)

т.е. передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев.

Следует подчеркнуть, что при последовательном соединении минимально-фазовых звеньев полученная система также будет минимально–фазовой, т.е. ее передаточная функция не будет иметь ни нулей, ни полюсов с положительной вещественной частью. Эквивалентная передаточная функция будет иметь диполь, если нуль одного звена компенсирует полюс другого.

При параллельном соединении на входы всех звеньев подается одна и та же величина, а выходные величины суммируются с соответствующими знаками (рис.2.15,б). Здесь и далее суммирующее звено будем изображать в виде круга, разделенного на четыре сектора. Если к сектору подается «вычитаемое», то его затемняют (рис.2.15,в) или перед соответствующим входом ставят минус.

Из схемы рис.2.15,б следует, что

y(p)=y₁(p) + y₂(p)=W₁(p) x(p) + W₂(p) x(p),

или .

В общем случае

(2.13)

т.е. передаточная функция параллельно соединенных звеньев равна алгебраической сумме передаточных функций всех звеньев, входящих в соединение. Если и , то

.

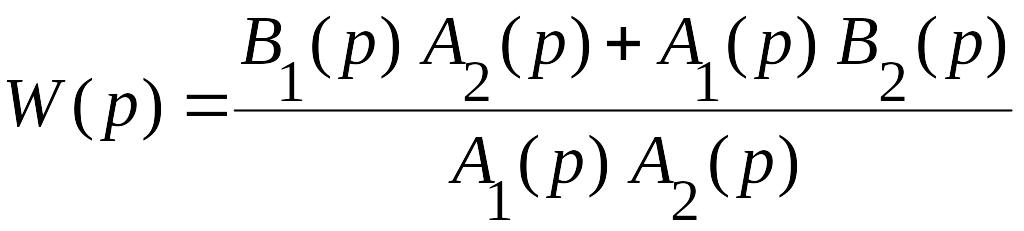Следовательно при параллельном соединении устойчивых звеньев эквивалентное звено также оказывается устойчивым, т.к. общий знаменатель суммы дробей не может иметь никаких корней, кроме корней слагаемых. Однако параллельное соединение минимально-фазовых звеньев может создать неминимально–фазовую систему. Эквивалентная передаточная функция имеет диполь, если звенья имеют одинаковые полюсы.

Соединение с обратной связью (параллельное встречное соединение) (рис.2.15,в) включает в себя цепь прямой передачи сигнала, в которую в рассматриваемом примере входит звено W₁(p), и обратную связь со звеном W₂(p). Если знак сигнала обратной связи y₁(p) положителен, то обратная связь называется положительной; в противном случае – отрицательной.

В автоматике наибольшее применение нашли системы с отрицательной обратной связью. В этих системах сигнал рассогласования е(р) равен

e(p)=v(p) – y₁(p),

где v(p) – входной сигнал.

Для систем с положительной обратной связью

e(p)=v(p)+y₁(p).

Эти уравнения называют уравнениями замыкания или уравнениями сравнивающего элемента.

Система с обратной связью является замкнутой. Передаточные функции замкнутых систем будем обозначать двумя индексами, первый из которых определяет выходную координату, а второй – входную. При этом передаточная функция системы, показанной на рис.2.15,в, будет иметь обозначение W_yv(p).

Для вывода формулы, связывающей W_yv(p) с W₁(p) и W₂(p), исключим из уравнения замыкания y₁(p) и e(p), имея в виду, что

y₁(p)= W₂(p) y(p),

e(p)= .

Для системы с отрицательной обратной связью получим

= ,

или . (2.14)

Для системы с положительной обратной связью в знаменателе будет знак минус. Таким образом, передаточная функция замкнутой системы с отрицательной обратной связью равна передаточной функции прямой цепи, деленной на единицу плюс произведение передаточных функций, образующих замкнутый контур. Произведение передаточных функций, входящих в прямую цепь передачи сигнала и обратную связь, называют передаточной функцией W(p) разомкнутого контура:

W(p)=W₁(p) W₂(p).

Из передаточной функции (2.14) следует, что нули W_yv(p) совпадают с нулями W₁(p) и полюсами W₂(p), однако полюсы функции W_yv(p) в общем случае отличаются от полюсов W₁(p) и W₂(p).

Передаточная функция

(2.15)

имеет диполь, если нуль звена прямого канала равен полюсу звена обратной связи. При наличии диполя в W(p) разомкнутого контура диполь будет и в передаточной функции замкнутой системы. Все типовые соединения звеньев помимо указанных ситуаций имеют диполи, если одно из звеньев соединения имеет диполь.

Знаменатель (2.15) является характеристическим полиномом замкнутой системы

(2.16)

Приравнивая к нулю, получим характеристическое уравнение

(2.17)

Из выражения для комплексного коэффициента передачи

следует, что в области частот, в которой выполняется условие

,

можно пренебречь обратной связью, полагая

.

Усиление разомкнутого контура считается малым, т.е. , если

,

что обычно имеет место в области высоких частот.

В области частот, где усиление велико

частотная характеристика системы определяется звеном обратной связи

.

Правила преобразования структурных схем. Структурные преобразования рационально выполнять в следующей последовательности: типовые соединения звеньев заменяют эквивалентными передаточными функциями; переносят звенья через сумматоры или узлы ветвлений сигналов или сумматоры через узлы ветвлений так, чтобы получить вновь типовые соединения. Эти операции продолжают до сведения исходной структуры, в зависимости от поставленной цели, к простейшим замкнутой или разомкнутой схемам. Преобразования обычно упрощаются, если звенья переносят через сумматоры или узлы ветвлений так, чтобы можно было объединить соседние сумматоры или узлы ветвлений.

Если ввести понятие направления ветвления, указывающее направление разделения (ветвления) сигнала на составляющие, то правила перемещения звена через узел и сумматор можно обобщить. Направление разделения (ветвления) сигнала будем указывать двойной стрелкой, а передачи сигнала – обычной стрелкой. Правила структурных преобразований удобно свести в таблицу 2.2.

Динамическая эквивалентность структур до и после преобразования может быть проверена с помощью алгебраических уравнений, описывающих эти схемы (см.таблицу 2.2).

Таблица 2.2