§2.3 Типовые звенья и их характеристики

Системы и соответствующие им звенья могут описываться дифференциальными уравнениями высокого порядка. Собственные операторы и операторы воздействия уравнений высокого порядка, как известно из курса алгебры, можно разложить на множители не выше второго порядка:

.

Для минимально–фазовых звеньев, т.е. звеньев, у которых нули и полюсы не имеют положительных вещественных частей, существует однозначная связь между и , и . Поэтому анализ и синтез минимально фазовых САУ можно проводить, используя, например, только ВЧХ или АЧХ . Обычно используют АЧХ.

Минимально–фазовые звенья не выше второго порядка относят к обыкновенным типовым динамическим звеньям.

Неминимально фазовые звенья, неустойчивые звенья (один или несколько полюсов имеют положительную вещественную часть), звенья с распределенными параметрами (иррациональные – с подкоренными выражениями) и трансцендентные звенья (содержат ) образуют группу особых типовых динамических звеньев. К этой группе иногда относят и дискретные звенья с модулированным сигналом. Особые звенья составляют основу особых линейных систем управления: САУ с переменными параметрами, с запаздыванием и распределенными параметрами.

В этом параграфе рассматриваются обыкновенные типовые динамические звенья, которые для сокращения именуются просто типовыми звеньями, и трансцендентное звено – звено запаздывания.

Типовые звенья являются основными составными частями алгоритмических структур непрерывных систем управления, поэтому знания их характеристик существенно облегчает анализ и синтез систем.

Общие свойства типовых звеньев и их классификация. Для типовых звеньев характерно наличие одной входной и одной выходной координат. Типовые звенья являются звеньями направленного действия, т.е. звеньями, в которых входная переменная влияет на выходную.

Передаточная функция любого из типовых звеньев является частным случаем следующей передаточной функции:

.

Типовые звенья подразделяются на позиционные (статические), интегрирующие и дифференцирующие.

Приведенная передаточная функция соответствует наиболее сложному из типовых позиционных звеньев. Наибольший практический интерес представляют простейшие (элементарные) позиционные звенья:

- безынерционное (пропорциональное);

- апериодическое (инерционное) 1-го порядка;

- колебательное;

- консервативное.

Если относительный коэффициент демпфирования , характеризующий колебательность звена, становится равным или превышает 1, то колебательное звено переходит в апериодическое звено второго порядка:

К типовым интегрирующим звеньям относятся:

– идеальное,

– реальное (инерционное).

Типовые дифференцирующие звенья также разделяются на идеальные и реальные

Свойства всех звеньев будем изучать в следующей последовательности.

Исходя из определения передаточной функции

,

где и - изображение входной и выходной координат, записываем уравнение связи

Заменяя в W(p) оператор p на символ дифференцирования и одновременно меняя y(p) на y(t) и x(p) на x(t), получаем оригинал уравнения связи. Пусть W(p)=b(p)/c(p), тогда уравнение связи имеет вид:

c(p)y(t)=b(p)x(t), где р=d/dt.

Используя обратные преобразования Лапласа, определяем переходную и весовую функции ; .

Заменяя в W(p) оператор p на j , получим комплексный коэффициент передачи .

Записывая W(j ) в показательной W(j )=A( )e и алгебраической формах W(j )=U( )+jV( ), определим амплитудно–частотную A( ), фазо–частотную , вещественную частотную и мнимую частотную функции. По полученным выражениям построим временные и частотные характеристики, включая логарифмическую амплитудно–частотную характеристику (ЛАЧХ):

L( )=20 lg .

Пропорциональное звено. Связь между мгновенными значениями входной x(t) и выходной y(t) координат пропорционального (безынерционного) звена описывается алгебраическим уравнением.

Полагая х(t)=K1₀(t) и х(t)= (t), будем иметь:

h(t)=K1₀(t); W(t)=K (t).

Частотные характеристики

W (j )=W(p) =K; A( )= ;

p=j

=arg W(j )=0; U( )=K; V( )=0; L( )=20 lgA( )=20 lgK.

Важный результат следует из анализа A( ) и : безынерционное звено пропускает сигналы любой частоты с одинаковым коэффициентом передачи (усиления или ослабления) и не создает фазового сдвига между входным и выходным сигналами. Характеристики безынерционного звена приведены на рис.2.5.

Следует отметить, что понятие безынерционного звена является математической идеализацией, поскольку все реальные технические элементы обладают определенной инерционностью, препятствующей мгновенной передаче энергии или вещества со входа на выход элемента. Если инерционность элемента на два-три порядка меньше, чем у остальных элементов рассматриваемой системы, то его можно считать безынерционным. К безынерционным элементам часто относят: операционный усилитель, используемый в режиме масштабного усилителя; блок умножения дискретных сигналов; редуктор; делитель напряжения; тахогенератор, используемый в качестве датчика частоты вращения инерционного объекта.

Рис.2.5 Характеристики безынерционного звена

Апериодическое звено первого порядка. Исходя из определения передаточной функции ,

получим уравнение связи (Tp+1)y(p)=Kx(p).

Заменяя y(p) на y(t), x(p) на x(t) и принимая p за символ дифференцирования, получим дифференциальное уравнение (Tp+1)y(t)=Kx(t), где p= .

Используя таблицы обратного преобразования Лапласа, определим переходную и весовую функции

;

.

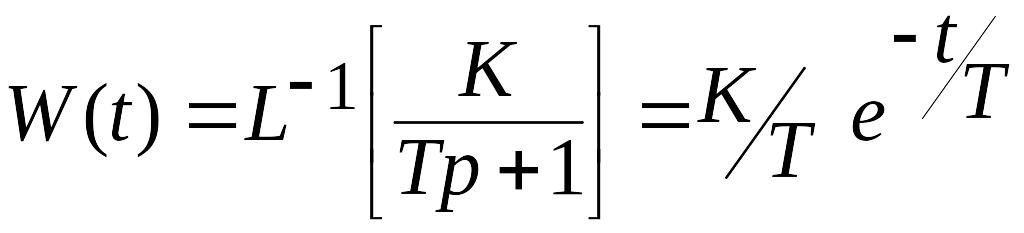Аналогичный результат, естественно, должен получиться, если дифференциальное уравнение решать классическим способом, в соответствии с которым при x(t)=1₀(t) решение неоднородного уравнения – равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения : .

задается в виде экспоненты , где c – постоянная интегрирования, – корень характеристического уравнения. проще найти, рассматривая установившийся режим работы, т.е. полагая . При этом , окончательно получаем с учетом нулевых начальных условий , где символ опущен.

Комплексный коэффициент передачи

,

т.е. ; .

АЧХ является модулем , т.е.

,

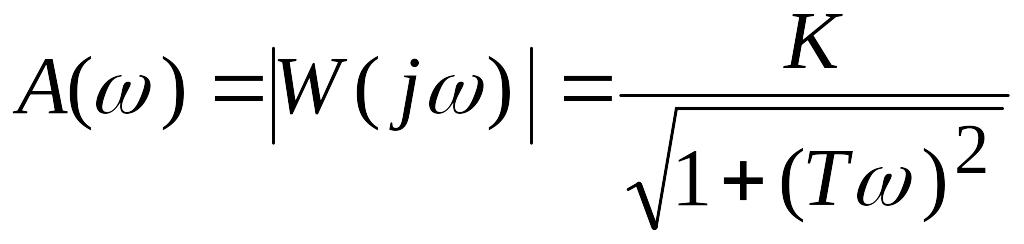а ФЧХ – аргументом : .