§10. Численное интегрирование. Формулы Ньютона-Котеса. Оценка погрешности квадратурных формул

При изложении ответа на этот вопрос следует дать математическую постановку задачи численного интегрирования и идею ее решения, ввести понятия квадратурной формулы, получить формулы Ньютона-Котеса и их частные случаи, вывести оценку погрешности квадратурных формул.

Задача численного интегрирования функции заключается в вычислении значений определенного интеграла, когда известен ряд значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой, двойного – механической кубатурой. Соответствующие формулы называются квадратурными и кубатурными.

Обычный прием механической квадратуры заключается в том, что данную функцию f(x) на рассматриваемом отрезке [a,b] заменяют интерполирующей или другой аппроксимирующей функцией φ(x) простого вида (например, полиномом), а затем приближенно полагают

. (22)

φ(x) такова, что интеграл в правой части (22) вычисляется непосредственно. Формулы вида (22) для приближенного вычисления интегралов, которые получаются заменой подынтегральной функции интерполяционным полиномом Лагранжа с равноотстоящими узлами, называются формулами Ньютона-Котеса.

Пусть , , . Заменяя функцию f(x) полиномом Лагранжа, получим приближенную квадратурную формулу:

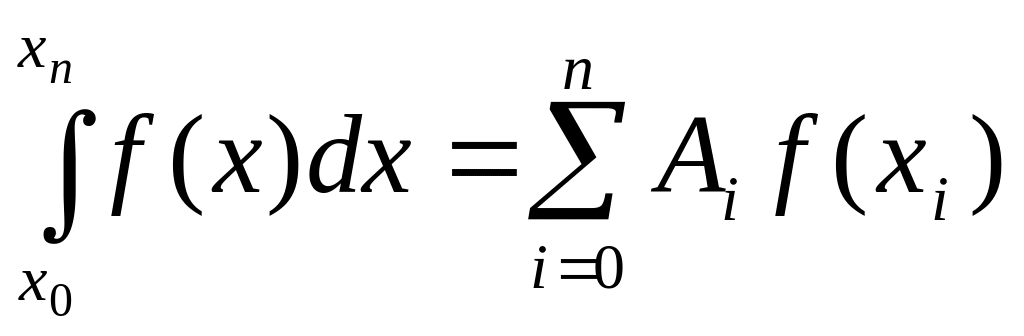, (23)

где A_i – некоторые постоянные коэффициенты. Получим для них явные выражения. Запишем полином Лагранжа в виде:

,

где . Введя обозначения и , получим

.

Отсюда .

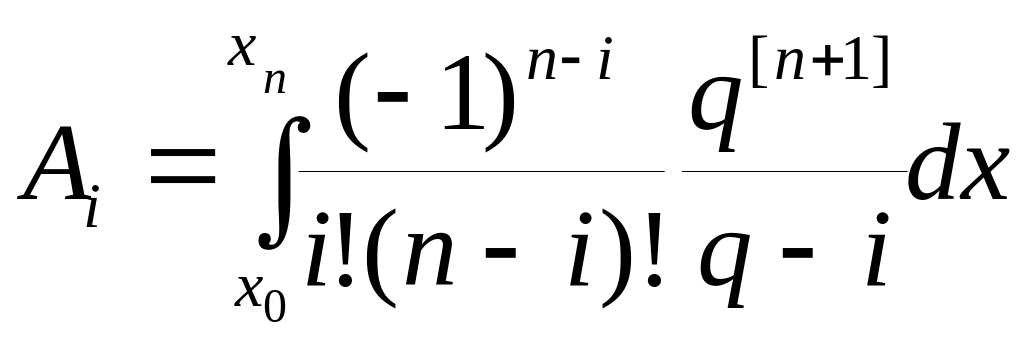Так как , сделав замену переменной в определенном интеграле, получим . Используя выражение , записывают , i= 0, 1, …, n, где , - постоянные, называемые коэффициентами Котеса. Квадратурная формула (23) при этом приобретает вид . H_i не зависят ни от подынтегральной функции, ни от промежутка интегрирования и могут быть вычислены раз навсегда. Нетрудно убедиться, что 1) , 2) H_i=H_n-i.

Частными случаями формул Ньютона-Котеса являются формула трапеций (при n=1) и формула Симпсона (n=2), которые на практике используются в виде обобщенной формулы трапеций:

, (24)

где m – число разбиений отрезка интегрирования, и обобщенной формулы Симпсона

. (25)

Заметим, что в формуле Симпсона число разбиений отрезка интегрирования является четным.

§11. Классификация и общая характеристика методов решения дифференциальных уравнений. Хорошо и плохо обусловленные задачи

При изложении ответа на этот вопрос следует дать определения основным понятиям теории дифференциальных уравнений: дифференциальное уравнение, обыкновенное и в частных производных; его общее и частное решение, постановка задачи для дифференциального уравнения, дополнительные условия; методы решения, их классификация и общая характеристика, понятие устойчивости задачи.

Уравнения, в которых неизвестные функции входят под знак производной, называют дифференциальными. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Дифференциальным уравнением с частными производными называется уравнение, включающее, по меньшей мере, одну частную производную от неизвестной функции двух или более независимых переменных.

Дифференциальное уравнение, как обыкновенное, так и с частными производными, имеет в общем случае бесчисленное множество решений. Поэтому, если физический процесс описывается с помощью дифференциального уравнения, то для однозначной характеристики этого процесса к уравнению нужно присоединить какие-то дополнительные данные. Таким образом, полная математическая постановка задачи содержит дифференциальное уравнение и дополнительные условия, позволяющие выделить единственное решение среди семейства решений этого уравнения. Дополнительные условия задаются обычно на границе области G. Эти дополнительные данные в простейшем случае состоят из начальных и краевых (граничных) условий. В сущности, различить их можно лишь в том случае, когда одна из независимых переменных играет роль времени, а другая – пространственной координаты (для случая двух независимых переменных). При этом условия, относящиеся к начальному моменту времени, называются начальными, а условия, относящиеся к фиксированным значениям координат (обычно это координаты граничных точек рассматриваемого линейного континуума), - краевыми. Решение требуется найти в некоторой области изменения независимых переменных G(t, x,…). Методы решения можно разделить на точные, приближенные аналитические и численные.

К точным относятся методы, позволяющие выразить решение дифференциального уравнения через элементарные функции либо представить его при помощи квадратур от элементарных функций. Нахождение точного общего решения дифференциального уравнения облегчает качественное исследование этого решения и его дальнейшую обработку. Однако классы уравнений, для которых разработаны методы получения точных решений, узки и охватывают лишь малую часть возникающих на практике задач. Например, доказано, что решение уравнения не выражается через элементарные функции, а уравнение можно точно проинтегрировать и найти общее решение .Однако для вычисления значения надо численно решить трансцендентное уравнение, таким образом, задача сводится к не менее сложной.

Приближенными аналитическими будем называть методы, в которых решение получается как предел некоторой последовательности , где выражаются через элементарные функции или с помощью квадратур. При конечном значении n получаем приближенное выражение для .

Численные методы – это алгоритмы вычисления приближенных значений искомого решения на некоторой выбранной конечной сетке аргументов. Решение при этом получается в виде таблицы.

Приближенные аналитические и численные методы не позволяют найти общего решения дифференциального уравнения, они могут дать только какое-то частное решение. Это их основной недостаток. Зато эти методы применимы к очень широким классам уравнений и всем типам задач для них. Поэтому с появлением быстродействующей вычислительной техники эти методы стали основным способом решения конкретных практических задач.

Численные методы можно применять только к корректно поставленным (или регуляризованным) задачам. Однако для успешного применения этих методов формального выполнения условий корректности может оказаться недостаточным. Надо, чтобы задача была хорошо обусловленной (устойчивой), т.е. малые изменения исходных данных приводили бы к малым изменениям результатов. Если это не так, т.е. задача плохо обусловлена (слабо устойчива), то небольшие изменения исходных данных или эквивалентные им вычислительные погрешности могут сильно исказить решение.

В качестве примера плохой обусловленности рассмотрим задачу: . Общее решение: , из начального условия находим С=0, следовательно, .

Изменим начальное условие: . Тогда С=10^-6 и , т.е. решение изменилось очень сильно.