§4. Решение систем линейных алгебраических уравнений.

Классификация численных методов

При изложении ответа на этот вопрос следует отметить, что разработано множество различных численных методов решения систем линейных алгебраических уравнений. Выбор того или иного метода в конкретном случае определяется свойствами матрицы системы. Охарактеризовать прямые и итерационные методы, указать достоинства и недостатки методов, относящихся к указанным классам, привести примеры.

К решению систем линейных алгебраических уравнений с большим числом неизвестных приводят многие практически важные задачи. Разработано множество методов, предназначенных для решения систем с матрицей того или иного вида. Все эти методы можно разделить на два больших класса: прямые (или точные) и итерационные.

Прямые методы дают решение системы за конечное число арифметических операций. Если коэффициенты системы не содержат погрешностей, а арифметические операции выполняются точно (без округления), то решение получается точным. К прямым методам относятся: метод Гаусса и его многочисленные модификации (например, метод главного элемента, метод квадратного корня, метод отражений, метод прогонки и т.д.), метод Крамера, методы ортогонализации. Недостатки прямых методов: иногда требуется выполнение неприемлемо большого числа арифметических и логических операций; погрешности округления могут очень сильно исказить результат.

Итерационные методы позволяют получить приближенное решение с любой заданной точностью ε. Они дают искомое решение как предел последовательности приближений и различаются способами построения таких последовательностей. Недостатком этих методов является то, что построенные последовательности нередко оказываются расходящимися, т.е. конечного предела таких последовательностей может не существовать. Поэтому оказывается необходимым исследование сходимости. К итерационным методам относятся метод простой итерации, метод Зейделя, релаксационные методы, методы подпространств Крылова и многие другие.

§5. Метод Гаусса решения систем линейных алгебраических уравнений и его модификации

При изложении ответа на этот вопрос следует записать систему линейных алгебраических уравнений, рассказать о прямом и обратном ходе метода Гаусса, записать формулы прямого и обратного хода, перечислить некоторые модификации метода Гаусса и более подробно остановиться на методе трехдиагональной прогонки.

Дана система линейных алгебраических уравнений

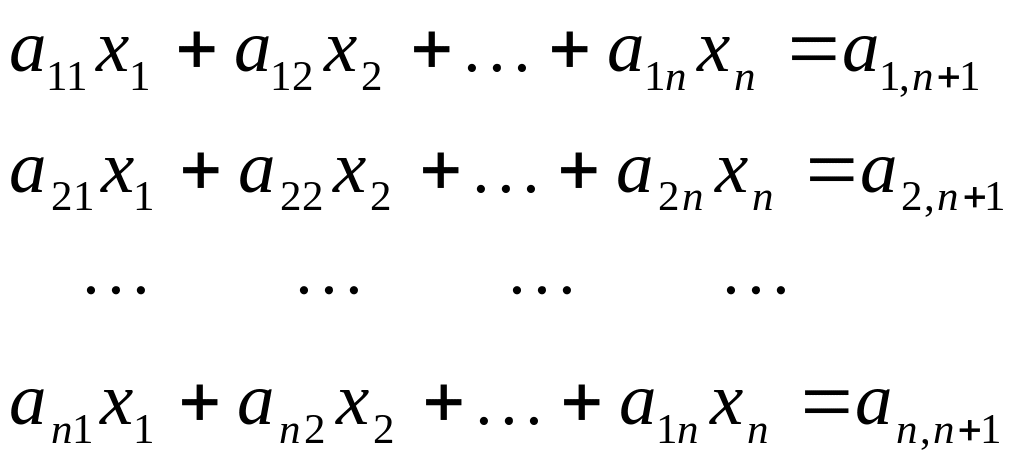
с квадратной неособенной матрицей, - неизвестные. Метод Гаусса (метод последовательного исключения неизвестных) состоит из прямого и обратного хода. В результате прямого хода матрица системы приводится к треугольному виду, а обратного - вычисляются значения неизвестных.

Формулы прямого хода метода Гаусса имеют вид

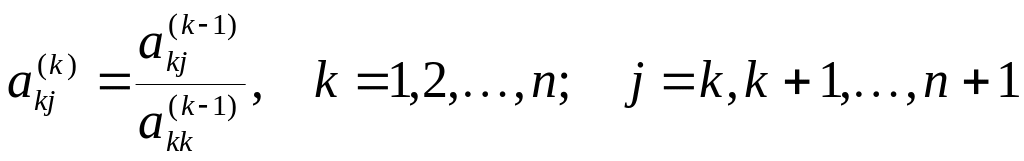
Формулы обратного хода метода Гаусса имеют вид

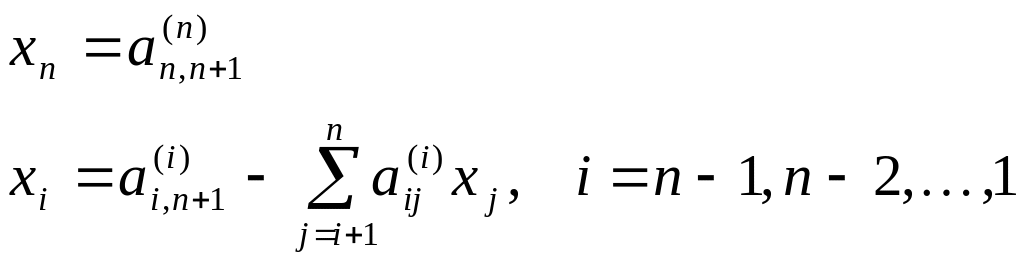
Метод Гаусса имеет множество модификаций, обусловленных, главным образом, свойствами матрицы системы: метод Гаусса с выбором главного элемента, метод квадратного корня, метод отражений и т.д. Очень часто используется метод прогонки, который применяется для решения систем с трехдиагональной матрицей. В целях экономии памяти компьютера такую систему записывают в виде: 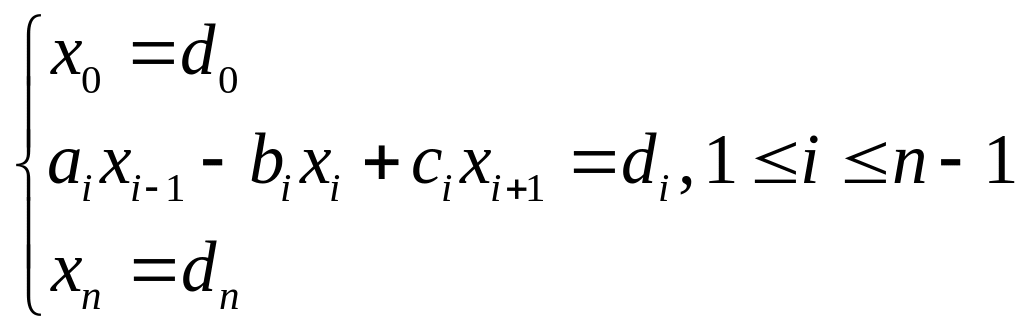(7)

Так как прогонка – частный случай метода Гаусса, различают прямую прогонку и обратную прогонку. Прямой ход сводится к исключению элементов a_i. В результате получается система, содержащая в каждом уравнении только два неизвестных x_i и x_i+1. Поэтому формулы обратного хода имеют вид:

(8)

Таким образом, в ходе прямой прогонки следует определить коэффициенты p_i+1 и q_i+1. Для этого в формуле (8) уменьшим индекс i на 1:

(9)

и подставим выражение (9) в уравнение (7): .

Отсюда

(10)

Таким образом, формулы прямого хода имеют вид:

Для определения значений p₁ и q_1. используем первое уравнение системы (7): . Отсюда p₁ = 0 и q₁ = d₀. Значение x_n получаем из последнего уравнения системы (7).