
- •2. Интерполирование при помощи алгебраических полиномов.
- •3. Интерполяционный полином Лагранжа.
- •4. Интерполяционный полином Ньютона.
- •5. Оценка остаточного члена интерполяционного полинома.
- •6. Численное интегрирование
- •7. Применение полинома Лагранжа
- •8. Формулы прямоугольников
- •9. Формула трапеций
- •10. Формула Симпсона
- •11. Оценка погрешности квадратурных формул
- •16.Аппроксимация обыкновенных и частных производных с помощью разложения в ряд Тейлора и ее порядок.
- •17, 18. Некорректность численного дифференцирования
- •20. Метод прогонки решения систем линейных алгебраических уравнений с трехдиагональной матрицей
- •21. Постановка задач для уравнений в частных производных
- •22. Классификация уравнений в частных производных второго порядка
- •23, 24. Метод сеток (метод конечных разностей) решения краевых задач для уравнений второго порядка в частных производных
- •XI,yi,,.
- •25. Аппроксимация дифференциальных уравнений разностными
Интерполирование функции. Общие понятия
На практике часто встречаются функции f(x), заданными для некоторого конечного множества значений аргументаxна отрезке [a,b],x0=a,xm=bтаблицами их значений:x= x0,x1,x2, …,xm, f(x) =y0,y1,y2, …,ym
Здесь y0=f(x0),y1=f(x1), …,ym=f(xm).
Такая таблица может быть получена, например, в результате измерения некоторой величины в определенные моменты времени.
В процессе расчетов иногда необходимымы значения f(x) для промежуточных значений аргумента, которых нет в таблице. В этом случае функциюf(x) заменяют приближенной функцией, например, строят функцию φ(x), которая в заданных точкахx0,x1, …,xm принимает значенияy0,y1, …,ym, а в остальных точках отрезка [a,b] приближенно представляет функциюf(x) с той или иной степенью точности. В расчетах функция φ(x) заменяет функциюf(x).
Задача построения такой функции φ(x) и оценки ее близости к функцииf(x) называется задачейинтерполирования. Функция φ(x) называетсяинтерполирующей функцией.
Интерполирование применяется и в том случае, когда известно аналитическое представление функции f(x), но вычисление каждого значения является трудно вычисляемым.
Итак, построение интерполирующей функции при заданных значениях y0,y1,y2, …,ymфункцииf(x) в точкахx0,x1,x2, …,xmотрезка [a,b] означает определение такой функцииφ(x), чтоφ(x)f(x) приx[a,b]φ(xi) =f(xi) =yi, приxi[a,b],i = 0, 1, …,m
Точки
![]() называютсяузлами интерполяции. А
их совокупность –интерполяционной
сеткой.
называютсяузлами интерполяции. А
их совокупность –интерполяционной
сеткой.
Для построения
интерполирующей функции используют
определенные системы линейно-независимых
функций, находящихся на этом отрезке:
φi(x),i = 0, 1, 2, …, записывая
функциюφ(x) в виде
линейной комбинации![]() ,
гдеa0,a1,a2, …,an– числа.
,
гдеa0,a1,a2, …,an– числа.
Определенные на
отрезке [a,b]
функцииφi(x),i
= 0, 1, 2, …,n, называются
линейно-зависимыми, если существуют
постоянныеa0,a1,a2,
…,an,
не равные нулю одновременно и такие,
что![]() для всехx[a,b].
В противном случае функцииφi(x),i
= 0, 1, 2, …,n, называются
линейно независимыми.
для всехx[a,b].
В противном случае функцииφi(x),i
= 0, 1, 2, …,n, называются
линейно независимыми.
Определенные на отрезке [a,b] функцииφi(x),i = 0, 1, 2, …,n, являются на отрезке [a,b] линейно зависимыми тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других.
Примерами таких систем определенных и линейно-независимых на отрезке [a,b] функций являются:
1) последовательность степеней x: 1,x, x2,x3, …;
2) последовательность тригонометрических функций: 1, sinx,cosx,sin2x,cos2x, …;
3) последовательность
показательных функций: 1,
![]() ,
,![]() ,
…, где {αi}
– некоторая числовая последовательность,
и т.д.
,
…, где {αi}
– некоторая числовая последовательность,
и т.д.
В случае построения
интерполирующей функции с помощью
определенной системы линейно-независимых
функций φi(x),i
= 0, 1, 2, … задача интерполирования
заключается в определении констант![]() ,
удов - их равенствам
,
удов - их равенствам![]() .
(1)
.
(1)
и оценке близости между функциями f и φ.
Таким образом, для
определения коэффициентов aiимеем систему изm+1
уравнений сn+1
неизвестными. Матрица этой системы
имеет вид: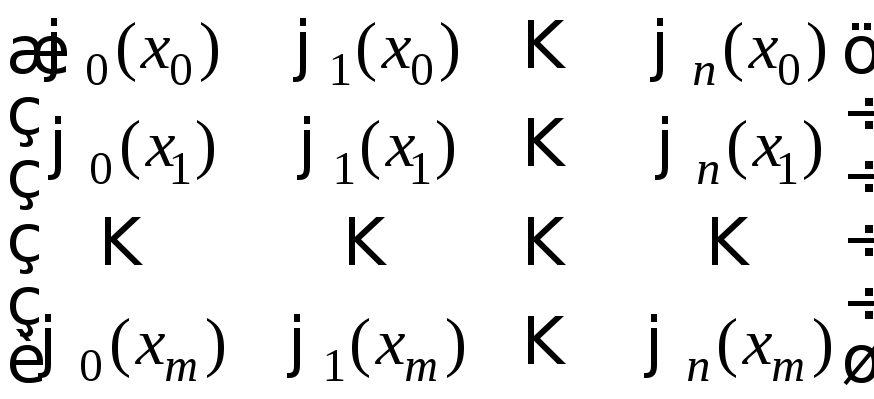
Для того, чтобы система линейных уравнений имела решение при любой правой части, достаточно, чтобы ранг ее матрицы был равен m+1. При этомn≥m. Решение будет однозначным приn=m.
Будем предполагать, что n =mи определитель системы (1) отличен от нуля. Тогда при любыхf(xj) система (1) будет иметь единственное решение.
2. Интерполирование при помощи алгебраических полиномов.
Интерполяция
алгебраическими
многочленами функцииf(x)наотрезке[a,
b]— построениемногочленаPn(x)степени
меньшей или равнойn, принимающего
в узлах интерполяции x0, x1,
...,xn значения f(xi):![]()
Система уравнений, определяющихкоэффициентытакого многочлена, имеет вид
![]()
Её определителемявляетсяопределитель Вандермонда
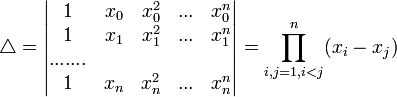
Он отличен от нуляпри всяких попарно различных значенияхxi, и интерполирование функцииfпо её значениям в узлахxiс помощью многочленаPn(x)всегда возможно и единственно.
3. Интерполяционный полином Лагранжа.
Полином Лагранжа
![]() имеет вид
имеет вид![]() ,
,
где
![]() ,i = 0, 1, …,n.
,i = 0, 1, …,n.
Имеем
![]() ,
i k,
,
i k,
![]() ,
i = 0, 1, …,n.
,
i = 0, 1, …,n.
Поэтому Ln(xi) =li (xi).
Коэффициент ciнаходятся из равенстваLn(xi) =yi.
Из этого равенства
следует
![]() .
.
С учетом этого
имеем:
![]() .
.
Чтобы записать
полином Ln(x)
в более компактном виде, вводится
обозначение![]() .
.
Тогда
![]() (3)
(3)
4. Интерполяционный полином Ньютона.
Полином Ньютона
имеет вид:
![]()
Коэффициенты
![]() находятся из равенствPn(xi)
=yi=f(xi):
находятся из равенствPn(xi)
=yi=f(xi):
a0=y0,
![]() =
=
![]() ,в числителе исправитьfнаy.
,в числителе исправитьfнаy.
….
![]() =
=![]()
….
Здесь
![]() разделенная
разность k-го
порядка.
разделенная
разность k-го
порядка.
С учетом этого
можно записать
![]() ,
,
В случае равноотстоящих
узлов интерполяции, т.е. когда
![]() ,
имеем
,
имеем
![]() (8)
(8)
где
![]() конечная
разность 1-го порядка.
конечная
разность 1-го порядка.
![]() =
=
![]()
![]() =
=
![]() 2-го порядка,
2-го порядка,
![]() =
=
![]()
![]() =
=
![]() 3-го
3-го
…
![]() конечная
разность k-го
порядка, k=2, 3,
...
конечная
разность k-го
порядка, k=2, 3,
...
Или
![]()
5. Оценка остаточного члена интерполяционного полинома.
Погрешность
интерполяционного полинома
![]() определяется выражением
определяется выражением![]() .
.
В узлах интерполяции
![]() .
В остальных точках
.
В остальных точках![]() .
.
Для получения
формулы оценки погрешности предположим,
что функция
![]() являетсяn+1 раз
непрерывно дифференцируемой, и рассмотрим
функцию
являетсяn+1 раз
непрерывно дифференцируемой, и рассмотрим
функцию![]() (5)
(5)
Эта функция
принимает в n+1 узлах
интерполяцииxiнулевые значения (u(xi)
= 0, т.к.Pn(xi)
=f(xi),n(xi)
= 0). Подберем коэффициентkтак, чтобы в некой точке![]() функцияu(x)
также принимала нулевое значение:
функцияu(x)
также принимала нулевое значение:![]() .(6)
.(6)
Предположим, что
![]() .
Тогда функция
.
Тогда функция![]() принимает нулевые значения на концах
каждого из (n+1) интервала
[
принимает нулевые значения на концах
каждого из (n+1) интервала
[![]() ],
[
],
[![]() ],…,[
],…,[![]() ],[
],[![]() ],…,[
],…,[![]() ].
Тогда согласно теореме (если непрерывно
дифференцируемая функция на концах
отрезка принимает одинаковые значения,
то внутри отрезка найдется по крайней
мере одна точка, в которой производная
равна нулю) первая производная
].
Тогда согласно теореме (если непрерывно
дифференцируемая функция на концах
отрезка принимает одинаковые значения,
то внутри отрезка найдется по крайней
мере одна точка, в которой производная
равна нулю) первая производная![]() имеет по крайней мереn+1
нулевое значение, вторая производная
имеет по крайней мереn+1
нулевое значение, вторая производная![]() имеет по крайней мереnи, наконец, (n+1)-я
производная
имеет по крайней мереnи, наконец, (n+1)-я
производная![]() имеет по крайней мере одно. Пусть
имеет по крайней мере одно. Пусть![]() .
Продифференцируем выражение (5) (n+1)
раз:
.
Продифференцируем выражение (5) (n+1)
раз:![]()
![]()
Подставив
![]() ,
получим
,
получим![]()
Отсюда
![]() (7)
(7)
Приравнивая правые
части равенств (6) и (7), получим
![]() .
.
Учитывая, что
![]() произвольная точка
из [a,b],
то можно записать
произвольная точка
из [a,b],
то можно записать![]() .
.
Введя обозначение
![]() ,
получим окончательно
,
получим окончательно![]() .
.
6. Численное интегрирование
Численное
интегрирование является одним из методов
вычисления определенного интеграла
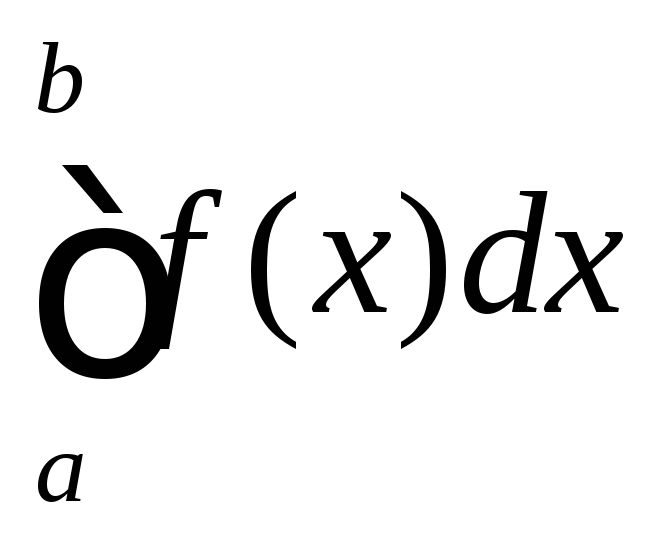 .
.
Если функция f(x)
непрерывна на отрезке [a,
b] и известна ее
первообразнаяf(x),
то можно воспользоваться формулой
Ньютона-Лейбница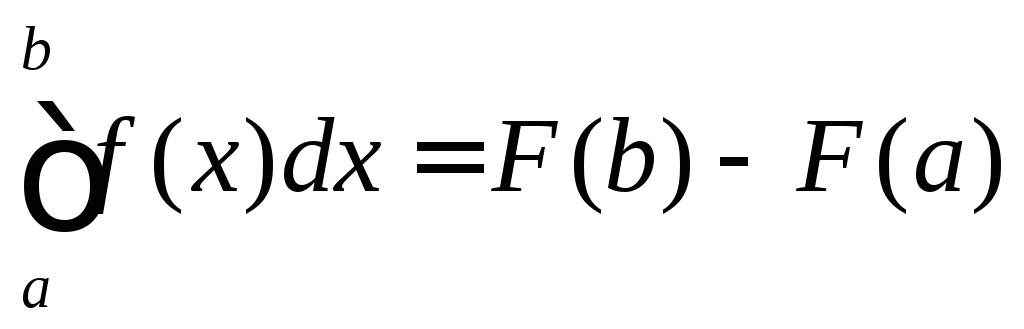 (1)
(1)
Однако зачастую первообразная f(x) неизвестна или является слишком сложной. В таких случаях, а также тогда, когда подынтегральная функцияf(x) задана таблично, и применяют численные методы.
Вычисление однократного интеграла называется механической квадратурой, а двойного –механической кубатурой. Соответствующие формулы называютсяквадратурными и кубатурными.
Обычный прием механической квадратуры заключается в том, что заданную таблично функцию f(x) на рассматриваемом отрезке [a,b] заменяют интерполирующей или другой аппроксимирующей функцией φ(x) простого вида (например, полиномом), а затем, с учетом того, чтоf(x) φ(x), приближенно полагают
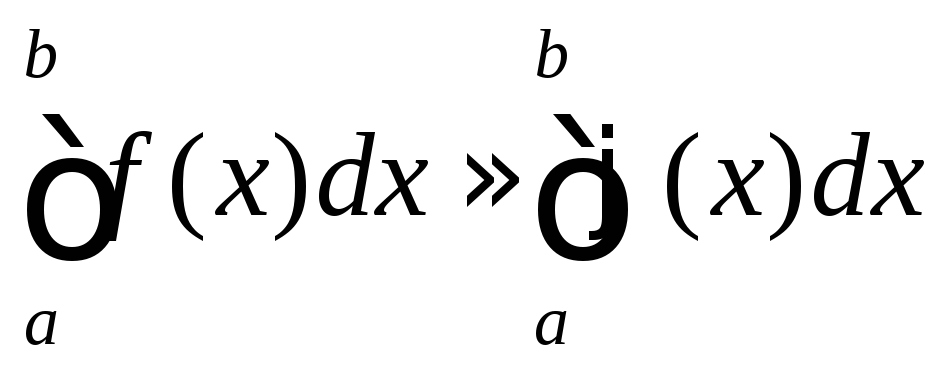 .
(2)
.
(2)
Обычно φ(x) такова, что интеграл в правой части (2) вычисляется непосредственно по формуле (1).
