16.Аппроксимация обыкновенных и частных производных с помощью разложения в ряд Тейлора и ее порядок.

Наиболее простые аппроксимационные выражения для производных функции f(x) получаются, когда в формуле (1) имеется только один член (т.е. когдаm=k):

(2)

…

Оценим погрешность этих выражений. Для этого воспользуемся разложением в ряд Тейлора

f(x_i) =f(x) +f (x) (x_ix) +f (x) (x_ix)²/ 2!+ … + f^(p)(x) (x_i  x)^p / p! + …

Имеем

f (x₀) = f (x) + f  (x) (x₀  x) + f  (x) (x₀  x)² / 2! + f⁽³⁾(x) (x₀  x)³ / 3! + …

f (x₁) = f (x) + f  (x) (x₁  x) + f  (x) (x₁  x)² / 2! +f⁽³⁾(x) (x₁x)³/ 3! + …

Отсюда

f (x₁)  f (x₀) = f  (x) (x₁  x₀) + f  (x) [(x₁  x)²  (x₀  x)²] / 2! + …

+ …

С учетом этого,

Аналогично можно показать, что

Исследуем точность выражения k-той производной функцииf(x), определяемой формулой (1), т.е. когда

Имеем

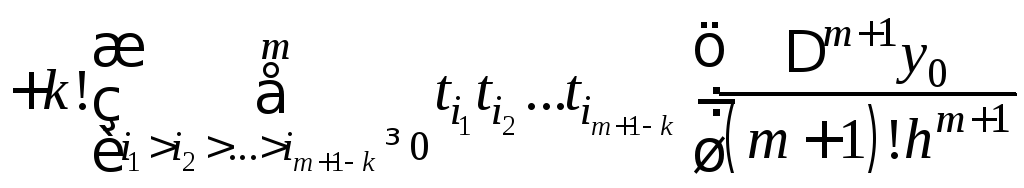
Аппроксимация полиномом (m+1)-го порядка точнее, чем полиномомm-го. Поэтому в качестве погрешности равенстваможно принять последнее слагаемое этого выражения. Если шаг таблицы достаточно мал, то можно записать

= 

 

т.е. =

=,

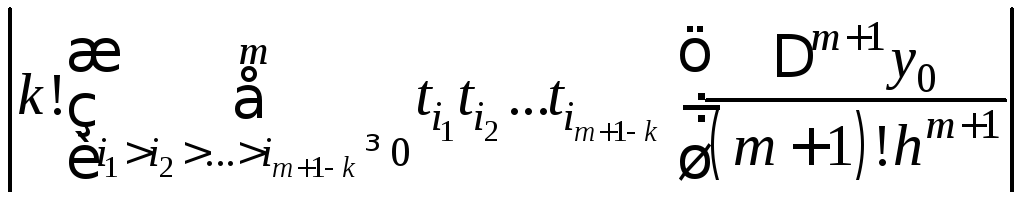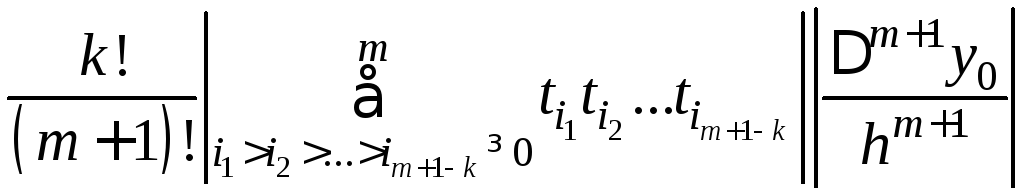
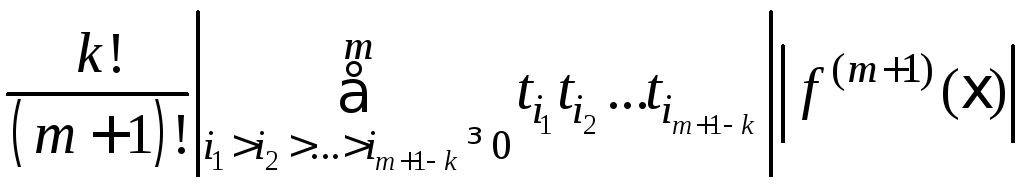где x₀x_m.

Учитывая, что xx_ix_mx₀=mh, можно записать

= 

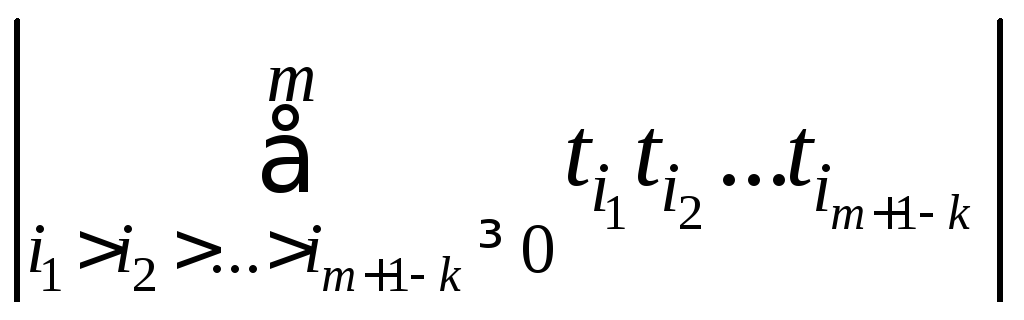 m^m+1kh^m+1k=O(h^m+1k)

С учетом этого получаем O(h^m+1k)

Таким образом, порядок точности формулы (1) по отношению к шагу hравен числу узлов интерполяцииm+1 минус порядок производнойk. Поэтому минимальное число узлов, необходимое для вычисленияk-й производной, равноk+1. В этом случае имеем формулы (2), аппроксимирующие производные с первым порядком точности. Эти выводы соответствуют общему принципу: при почленном дифференцировании ряда скорость его сходимости уменьшается.

17, 18. Некорректность численного дифференцирования

Рассмотрим погрешности численного дифференцирования. Выражение для производной k-го порядка можно записать следующим образом

=(3)

Здесь

c_i(x) =O(1),R_k(x) =O(h^m+1k)d_k(x)h^m+1k,d_k(x) =O(1).

Остаточный член R_k(x) определяет погрешность равенстваи неограниченно убывает приh → 0.

Обычно точные значения y(x_i) неизвестны, так что вместо (3) имеем

=

где y*(x) =y(x) + δy(x), т.е

=

Где

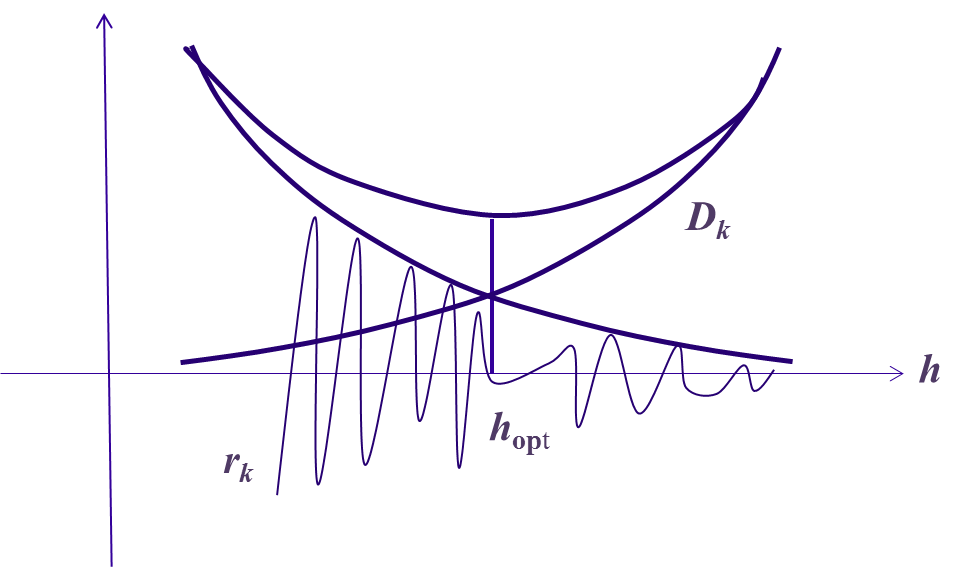
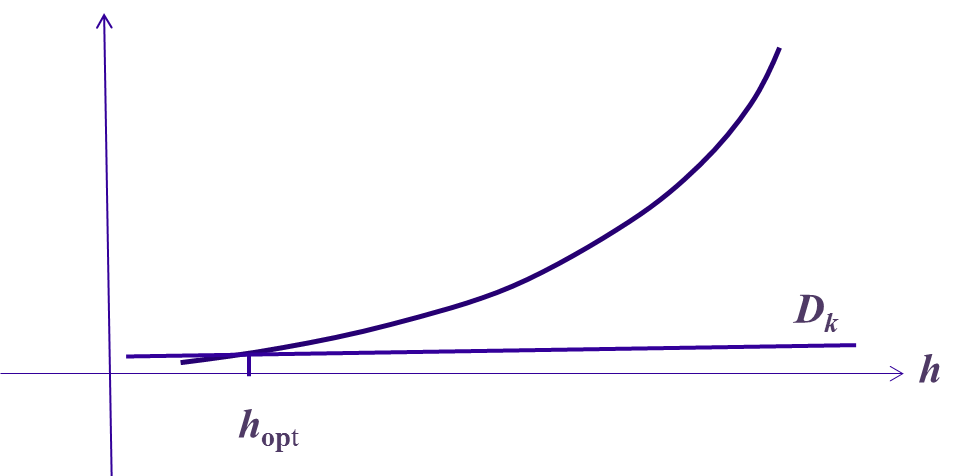
Рис.1. Погрешности дифференцирования. Рис.2. Погрешности интерполирования.

Погрешность δy(x) определяется либо погрешностью измерений, либо погрешностью вычислений (например, если сложно вычисляемая функция заменяется легко вычисляемой). В обоих случаях ее точный вид неизвестен. Ее мажоранта, где > 0, неограниченно возрастает приh→0. Фактически погрешностьнерегулярно зависит от величины шага, беспорядочно осциллируя в границах, определенных мажорантой. Пока шаг достаточно велик, имеем мажоранта< мажоранты, поэтому при его убывании, хотя мажорантаи растет, мажоранта полной погрешностиубывает за счет уменьшения мажоранты. При дальнейшем уменьшении шага погрешностьстановится заметной, что проявляется в не вполне регулярной зависимости производнойот величины шагаh. Наконец, при достаточно малом шаге погрешностьстановится преобладающей, и при дальнейшем уменьшении шага величина производнойстановится все менее достоверной. Полная погрешность определяется мажорантой суммыR_k+r_k. Оптимальным будет шагh_opt, соответствующий минимуму этой кривой.

Шаг h < h_optневыгоден, а меньшая погрешность, вообще говоря, недостижима (хотя отдельные вычисления случайно могут оказаться более точными, мы об этом не сможем узнать).

Минимальная ошибка тем меньше, чем меньше погрешность входных данных. При δy(x) → 0 можно получить сколь угодно высокую точность результата, если шагhстремится к нулю, будучи всегда не менееh_opt(δ) (h≥h_opt(δ)). Но если допуститьh<h_opt(δ), то результат предельного перехода может оказаться неправильным.

Эта тонкость связана с некорректностью задачи численного дифференцирования. Пусть погрешность входных данных

.

Тогда погрешность первой производной

.

При m→∞ погрешность функции в Чебышевской норменеограниченно убывает (), а погрешность производной в той же норме неограниченно растет (). Таким образом, малым изменениям входных данных соответствуют неограниченно большие изменения значения производной, т.е. операция численного дифференцирования некорректна. Особенно сильно это сказывается при вычислении производных высокого порядка.

Изложенный выше способ определения оптимального шага и запрещение вести расчет с шагом меньше оптимального есть способ регуляризации численного дифференцирования, называемый регуляризацией по шагу.

19. ЧисленнОе решениЕ краевых задач для обыкновенных дифференциальных уравнений

Краевая задача для обыкновенного дифференциального уравнения – это задача отыскания частного решения этого уравнения на отрезке [a,b], в которой дополнительные условия накладываются на значения искомой функции более чем в одной точке этого отрезка. Очевидно, что поставить краевую задачу возможно для уравнения порядка не ниже второго. Точное решение удается найти крайне редко. Одним из наиболее употребительных на практике численным методом решения краевых задач является метод конечных разностей. Он является общим методом для решения начально-краевых задач и позволяет без трудоемких выкладок, пользуясь сеткой с относительно большой длиной шага, получить достаточные для практических целей сведения о решении. Метод конечных разностей является численным методом, т.е. дает искомое решение в виде таблицы чисел.

Рассмотрим этот метод на примере решения краевой задачи для линейного дифференциального уравнения второго порядка , (1)

где p(x), q(x) и F(x) – заданные функции при на отрезке [a,b] с краевыми условиями одного из двух типов:(2a)

или (2b)

Будем предполагать, что заданные функции p(x),q(x) иF(x) имеют на [a,b] непрерывные производные второго порядка,q(x)≤0; α₀, β₀≥0,. При этих условиях решения краевых задач (1)-(2a) и (1)-(2b) будут иметь непрерывные производные до четвертого порядка включительно. Интервал (a,b), в котором требуется найти решение, разобьем наnравных частей длиныh=(b-a)/n. При этом точки разбиения имеют абсциссы. Совокупность этих точек называетсясеткойна интервале (a,b), сами точки –узлами, а величинаh – шагом сетки. y_i=y(x_i). В каждом из узловx₁,x₂, …,x_n-1заменим производные, входящие в уравнение, комбинацией значений решения в некоторых узлах сетки по формулам численного дифференцирования. Для получения этих формул рассмотрим разложения в ряды Тейлора

(3)

(4)

Пренебрегая в формуле (3) слагаемыми порядка hвыше первого, получаем приближенное выражение для первой производной(5)

Используя таким же образом формулу (4), получаем следующее приближенное выражение для первой производной (6)

Формула (5) называется аппроксимацией первой производной разностями вперед, а формула (6) – аппроксимациейразностями назад.

Вычитая равенство (4) из равенства (3) и пренебрегая слагаемыми порядка hвыше второго, получаем аппроксимацию первой производной с помощьюцентральных разностей:(7)

Таким образом, формулы (5) и (6) имеют точность порядка h, а формула (7) - порядкаh².

Складывая равенства (3) и (4) и пренебрегая слагаемыми порядка hвыше второго, получаем аппроксимацию второй производной:(8)

Формула (8) имеет точность порядка h².

Аналогично можно получить аппроксимацию производной любого порядка.

Подставим эти соотношения в уравнение (1):

или , (9)

где ,,,.

Запишем алгебраические уравнения вида (9) в каждой точке x_i, i=1,2,…,n-1 рассматриваемой сетки. В результате получим систему n-1 линейных алгебраических уравнений с n+1 неизвестными y₀, y₁, … y_n. Недостающие два уравнения можно получить, используя краевые условия (2a) или (2b).

Решая систему линейных алгебраических уравнений, найдем приближенное решение краевой задачи (1)-(2).

При таком подходе необходимо ответить на три вопроса:

1. Существует ли решение алгебраической системы типа (9)?

2. Как найти такое решение?

3. Сходится ли разностное решение к точному при ?

Существование. В системе (9) ,при. Таким образом, система имеет свойство диагонального преобладания. При этом ее решение существует и единственно.

Способ решения. Система (9) является трехдиагональной. Для решения таких систем разработан специальный метод прогонки, являющийся модификацией метода Гаусса.

Сходимость. Можно доказать, что при достаточно гладких и ограниченных коэффициентах уравнения (1) погрешность разностной схемы имеет порядок .