XI,yi,,.

При h = lсетка называетсяквадратной.

Узлы, расположенные внутри области G(т.е. не лежащие на границе), называютсявнутренними.Множество таких узлов обозначим_h. Узлы, находящиеся на границе, называютсяграничными. Их совокупность обозначим γ_h. Таким образом, объединение_hγ_hпредставляет собой разностную сетку.

Численное решение задачи (1), (2) методом конечных разностей заключается в отыскании определенной на множестве узлов _hγ_hсеточной функцииw_ij, являющейся приближением для значений функцииu(x,y) в соответствующих узлах, т.е. в отыскании значенийw_iju_ij=u(x_i,y_j) при (x_i, y_j)_hγ_h.

Для этого в каждом внутреннем узле сетки производные заменяются (аппроксимируются) разностными отношениями для сеточной функции w_ij. В результате такой замены в дифференциальном уравнении (1), определенном в областиG, получается совокупность конечно-разностных уравнений, определенных в узлах сетки_h. Эта совокупность разностных уравнений совместно с соотношениями, аппроксимирующими граничные условия на множестве узлов γ_h, называетсяразностной схемой.

Разностная схема представляет собой систему алгебраических уравнений.

Конфигурацию узлов, используемую для построения разностного уравнения в узле ij, называютшаблоном.

Разностная схема строится таким образом, чтобы получаемые в результате решения ее системы алгебраических уравнений (как правило, линейных) значения w_ijбыли бы приближенными значениямиu_ij, такими, что

 w_iju_ij_h0 приh, l0.

Другими словами, разностная схема строится так, чтобы по мере измельчения сетки численное решение в ее узлах становилось бы все более близким к решению краевой задачи. Имея сеточную функцию w_ij, близкую кu_ij, можно, используя, например, полиномиальную интерполяцию, получить определенную в областиGфункцию, являющуюся приближением для решенияu(x,y) краевой задачи (1), (2).

25. Аппроксимация дифференциальных уравнений разностными

Аппроксимация дифференциальных уравнений разностными заключается в том, что каждая производная, входящая в дифференциальное уравнение и краевые условия, заменяется (аппроксимируется) каким-либо разностным отношением. Такая замена осуществляется во всех внутренних узлах сетки и на границе сеточной области.

Аппроксимация производных не является однозначной. Ее можно осуществлять, применяя интерполяционные полиномы. И в этом случае она не однозначна. Например, учитывая, что

, ,,

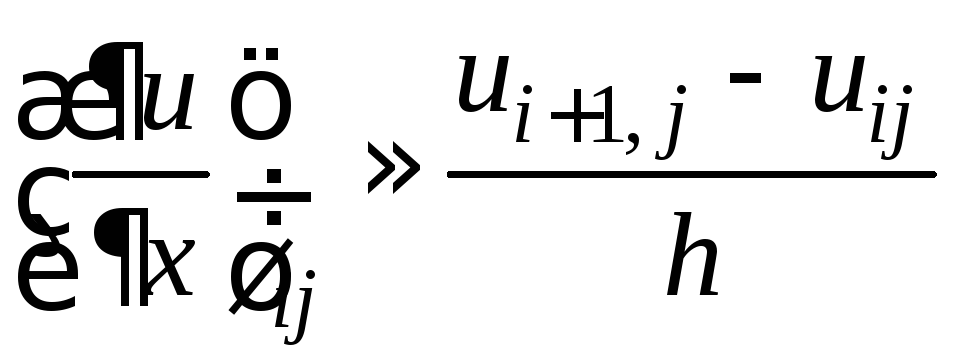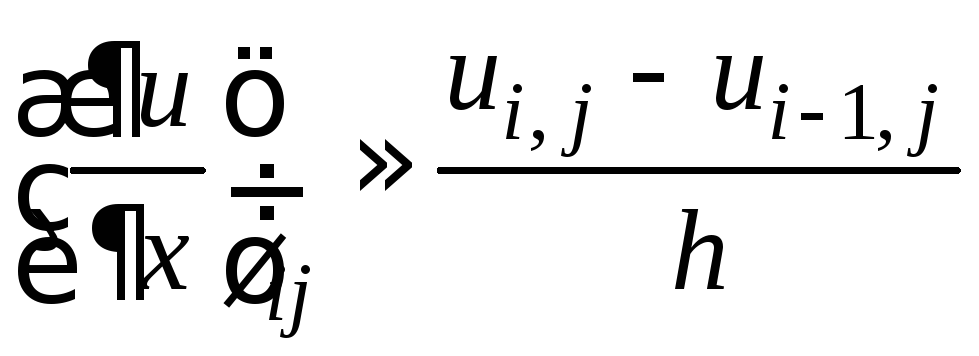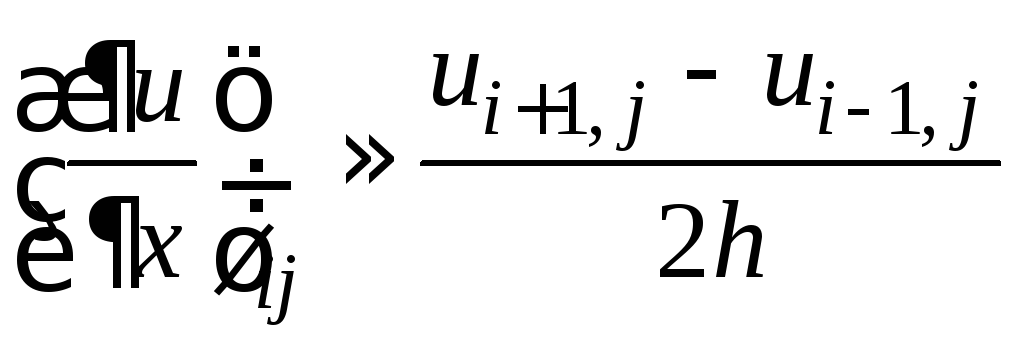и что w_iju_ij, производнуюможно заменить следующими тремя разностными отношениями (h=x_i+1x_iтакже конечная разность):

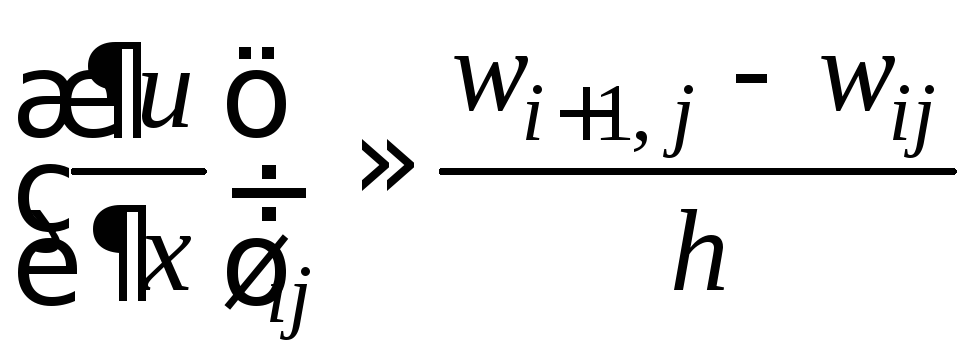(разностное отношение «вперед»),

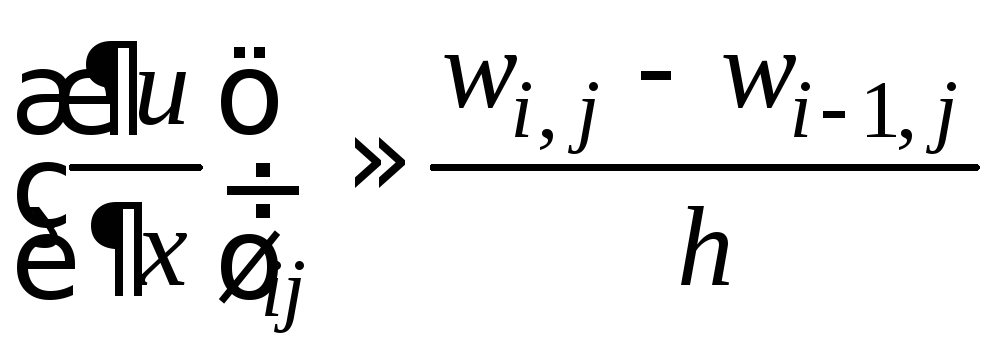(разностное отношение «назад»),

(центральное разностное отношение)

Аналогично для производной можно принять

, ,.

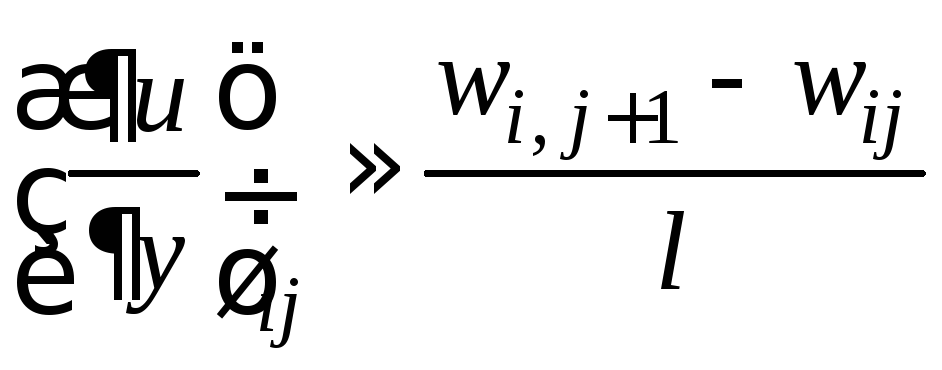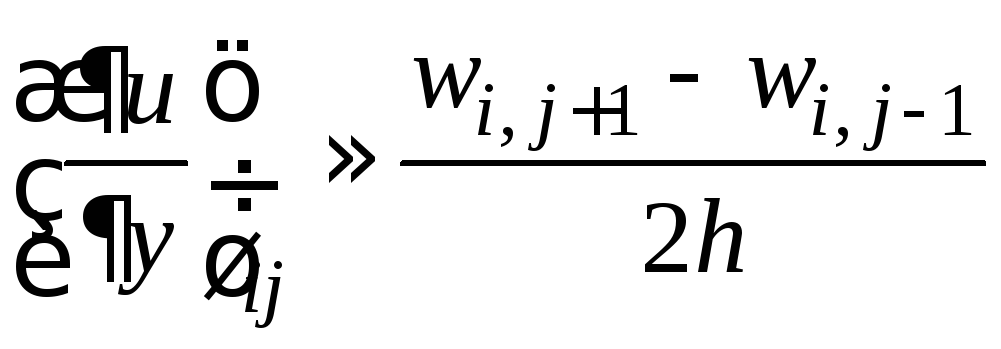Следуя такой же логике, частные производные второго порядка можно записать в виде

, .

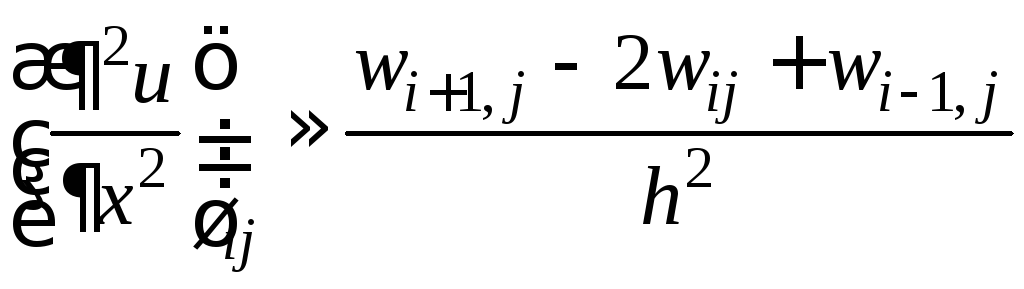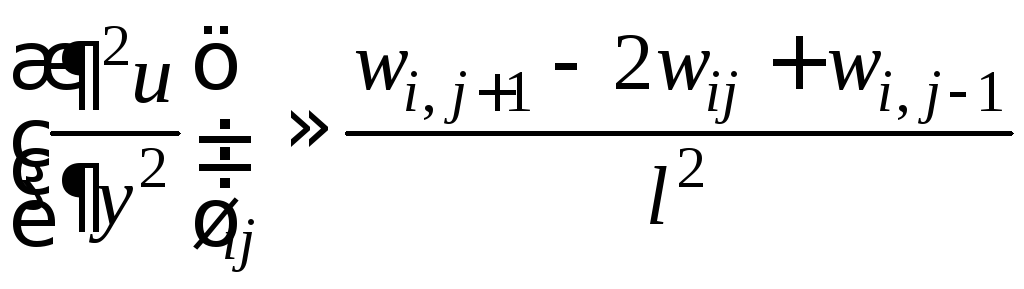В этом случае уравнение Лапласа (1) в узле ijзаменится следующим разностным уравнением

.

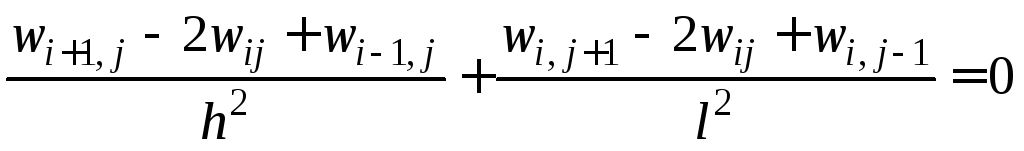Использованный при получении данного равенства шаблон носит название «пятиточечный шаблон крест».

Погрешность разностного уравнения, аппроксимирующего дифференциальное, определяется путем замены в разностном уравнении функции w_ij(приближенное численное решение) на функциюu_ij(точное численное решение) и последующей оценкой невязки_hполученного таким образом выражения с выражением дифференциального оператора в узлеijв рамках какой-либо сеточной нормы. В рассматриваемом случае уравнения Лапласа имеем

,

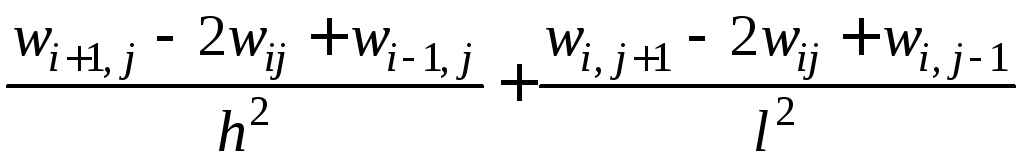
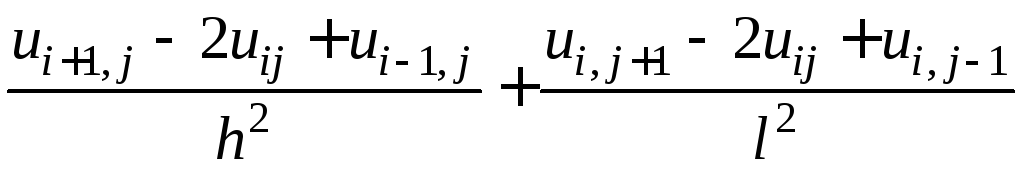_ij=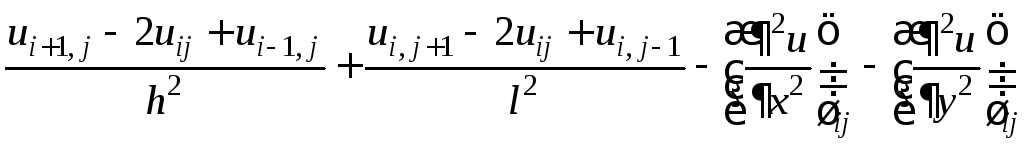

 _h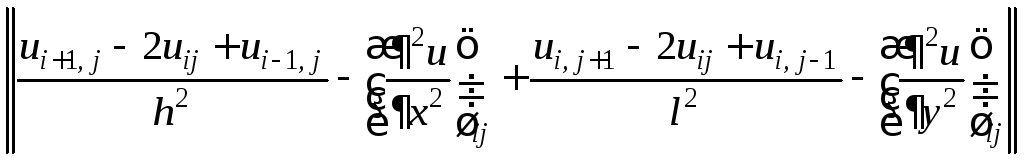==O(h²+l²)

Таким образом, схема крест для уравнения Лапласа имеет второй порядок аппроксимации относительно шагов сетки в обоих направлениях.

16