20. Метод прогонки решения систем линейных алгебраических уравнений с трехдиагональной матрицей

Наиболее важным частным случаем метода Гаусса решения систем линейных алгебраических уравнений является метод прогонки, применяемый к системам с трехдиагональной матрицей. Такие системы обычно записывают в каноническом виде:

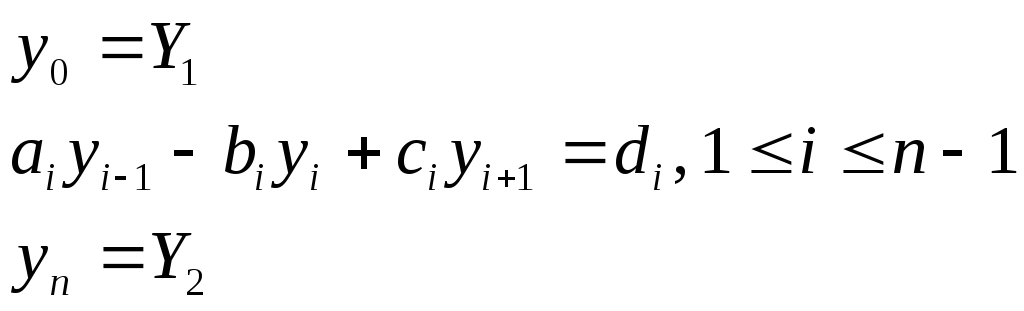(1)

Так как прогонка – частный случай метода Гаусса, различают прямую прогонку и обратную прогонку.

Прямой ход сводится к исключению элементов a_i. В результате получается система, содержащая в каждом уравнении только два неизвестныхy_iиy_i+1. Поэтому формулы обратного хода имеют вид:

(2)

Таким образом, в ходе прямой прогонки следует определить коэффициенты α_i+1иβ_i+1.

Уменьшим в формуле (2) индекс iна 1:(3)

и подставим выражение (3) в уравнение (1): .

Отсюда (4)

Для того, чтобы выражение (4) совпало с выражением (2), следует приравнять коэффициенты. Так получаем формулы прямого хода: (5)

Для начала вычислений прямой прогонки требуются значения α₁и β_1.Используя первое уравнение системы (1), получаем,

следовательно, α₁=0 и β₁=1, а для начала вычислений обратной прогонки требуется значениеy_n, которое дает последнее уравнение системы (1). Таким образом, при решении краевой задачи граничные условия дополняют разностную схему.

Покажем, что если выполнено условие преобладания диагональных элементов (6)

(причем хотя бы при одном iимеет место строгое неравенство), то в формулах прямого хода (5) не возникает деления на 0, и, следовательно, система (1) имеет единственное решение. Для этого предположим, что | α_i|<1 при некотором значении индекса. Тогда

Так как α₁=0, по индукции получаем, что | α_i|<1 при любом значенииi, а значит,для любогоi– что и требовалось доказать.

При выполнении условия (6) формулы прогонки устойчивы относительно ошибок округления и позволяют успешно решать системы уравнений с несколькими сотнями и тысячами неизвестных.

Условие (6) является достаточным, но не необходимым условием устойчивости прогонки. В практических расчетах для хорошо обусловленных систем типа (1) прогонка часто оказывается устойчивой даже при нарушении условия диагонального преобладания.

Вычисления по формулам прогонки (5), (4) требуют всего 3nячеек памяти и 9nарифметических операций (тогда как метод Гаусса с выбором главного элемента требуетn² ячеек памяти и ~2/3 n³ арифметических операций). Таким образом, метод прогонки значительно экономнее общего метода исключения неизвестных.

Метод прогонки позволяет найти и определитель матрицы исходной системы. Так как при исключении элементов a_iполучается система вида,

То .

21. Постановка задач для уравнений в частных производных

Независимыми переменными в физических задачах обычно являются время tи пространственные координатыx,y,z. Решениеu(x,y,z, t) ишется в некоторой области изменения независимых переменныхG(x,y,z, t) вида

G (x, y, z, t) = g (x, y, z)  [t₀, T],

т.е. в пространственной области g(x,y,z) на отрезке времениt₀tT.

Полная математическая постановка (формулировка) задачивключает дифференциальное уравнение и дополнительные условия, позволяющие выделить единственное решение среди семейства решений дифференциального уравнения. Дополнительные условия обычно задаются приt=t₀внутри областиg(x,y,z) и на ее границе(x,y,z) приtt₀.

Дополнительные условия, задаваемые внутри области g(x,y,z) приt = t₀, называютсяначальными условиями, а дополнительные условия, задаваемые на границе(x,y,z),граничными или краевыми условиями.

Задачу, у которой имеются только начальные условия, называют задачей Коши.

Задачу, у которой имеются только граничные е условия, называют краевойзадачей.

Задачу с начальными и граничными условиями называют смешанной краевой задачейилинестационарной краевой задачей.

Ограничимся рассмотрением корректно поставленных задач, т.е. таких задач, когда для некоторого класса начальных и граничных данных решение (в заданном классе функций) существует, единственно и непрерывно зависит от этих данных. Будем также предполагать, что решение непрерывно зависит от всех коэффициентов уравнения.