22. Классификация уравнений в частных производных второго порядка

Наиболее общее уравнение второго порядка с частными производными в случае двухнезависимых переменныхx,yимеет следующий вид

F(x, y, u_x, u_y, u_xx, u_xy, u_yy) = 0

а в случае переменных x,t– следующийF(x, t, u_x, u_t, u_xx, u_xt, u_tt) = 0.

В первом случае неизвестной функцией является функция u = u(x,y), а во втором – функцияu = u(x,t).

Различие этих и других уравнений состоит лишь в обозначении переменных.

Уравнения второго порядка классифицируются по знаку выражения (дискриминанта) B²– AC:

B²– AC < 0 –эллиптическийтип,

B²– AC = 0 –параболическийтип,

B²– AC > 0 –гиперболическийтип.

Физические процессы, описываемые разными типами уравнений, существенно отличаются друг от друга. Соответственно, постановки задач для них имеют свои особенности.

Заметим, что уравнение с переменными коэффициентами может иметь разный тип в разных точках x,t.

Уравнения с постоянными коэффициентами приводятся к следующим каноническим формам

u_xx+u_yy+au=f(x,y) (эллиптическийтип),

u_tu_xx+au=f(t,x) (параболическийтип)

u_ttu_xx+au=f(t,x) (гиперболическийтип),

Будем рассматривать простейшие формы этих уравнений

u_xx+u_yy= 0 (уравнениеЛапласа),

u_tu_xx= 0 (уравнениетеплопроводности)

u_ttu_xx= 0 (волновоеуравнение),

Для приведенных простейших уравнений второго порядка имеем соответственно

 AC< 0,AC= 0,AC> 0,

поэтому первое из них является эллиптическим, второе –параболическим, третье –гиперболическим.

Решения уравнения Лапласа называются гармоническими функциями. Например,u=ax+by+c,u=a(x²y²) +bx+cy+d.

Для уравнения Лапласа задается область с замкнутой границей и рассматриваются три вида краевых условий:

1-го рода (задача Дирихле) u_=(x,y), (x,y),

2-го рода (задача Неймана) u/n_=(x,y), (x,y),

и 3-го рода (смешанная краевая задача) (u+u/n)_=(x,y), (x,y),,константы.

Для волнового уравнения и уравнения теплопроводности задаются начальные условия при t=t₀.

При этом, если <x<, то получается задача Коши. Если жеa<x<b, то на концах отрезка [a,b] задаются граничные условия одного из трех указанных видов и задачаназывается начально-краевой или смешанной задачей Коши.

23, 24. Метод сеток (метод конечных разностей) решения краевых задач для уравнений второго порядка в частных производных

Рассмотрение метода конечных разностей начнем со следующей задачи Дирихле для уравнения Лапласа: найти решение u(x,y) уравнения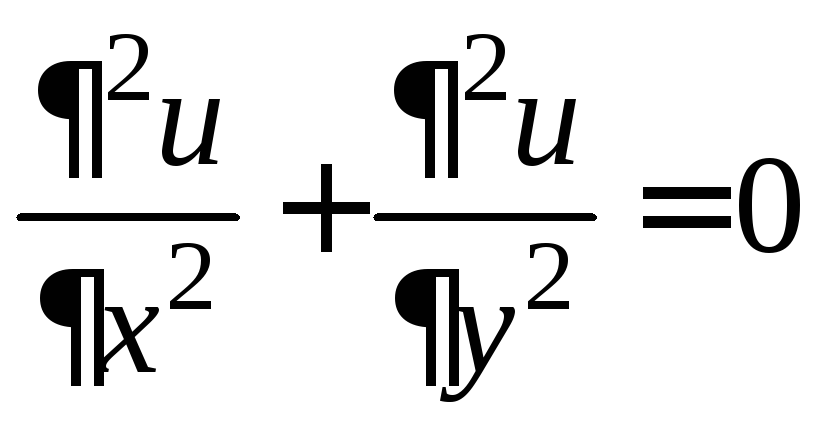(1)

в некоторой прямоугольной области G = [a, b] x [c, d] плоскости x, y при

, (2)

где функция φ (x, y) непрерывна на границе Г прямоугольника G.

Область Gс границей Г покроем прямоугольной сеткой. Для этого в плоскостиx,yпостроим два семейства параллельных прямых

; .

Здесь x₀=a,y₀=c– координаты левого нижнего угла прямоугольникаG,x_I=b, y_J=d– координаты его правого верхнего угла,h= (x_Ix₀)/Iиl= (y_Jy₀)/J–шаги сеткипо направлениямx иy соответственно.

Узлами сетки являются точки пересечения указанных прямых, имеющие координаты