7. Применение полинома Лагранжа

Пусть в n+1 узлахx_i,i=0, 1, …,nотрезка [a,b] известны значенияy_i=f(x_i), функцииy= f(x). Тогда, как известно, можно построить интерполяционный полином Лагранжа,

где ,i = 0, 1, …,n.

Имеем ,i k,

, i = 0, 1, …,n.

Поэтому L_n(x_i) =l_i (x_i).

Коэффициент c_iнаходятся из равенстваL_n(x_i) =y_i.

Из этого равенства следует .

С учетом этого имеем: .

Для того, чтобы записать полином L_n(x) в более компактном виде, вводится обозначение

.

Тогда 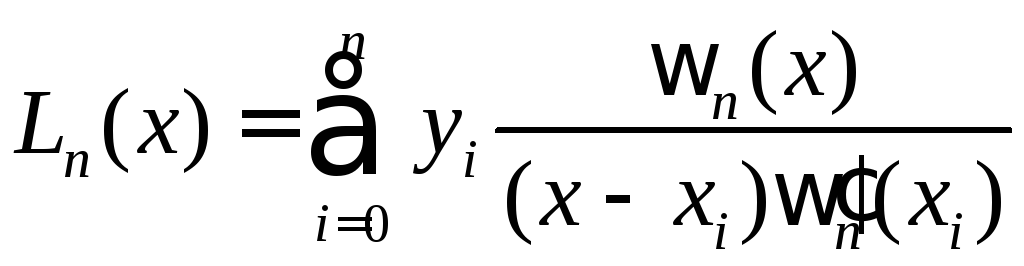(3)

При использовании полинома Лагранжа для расчета интеграла полагают

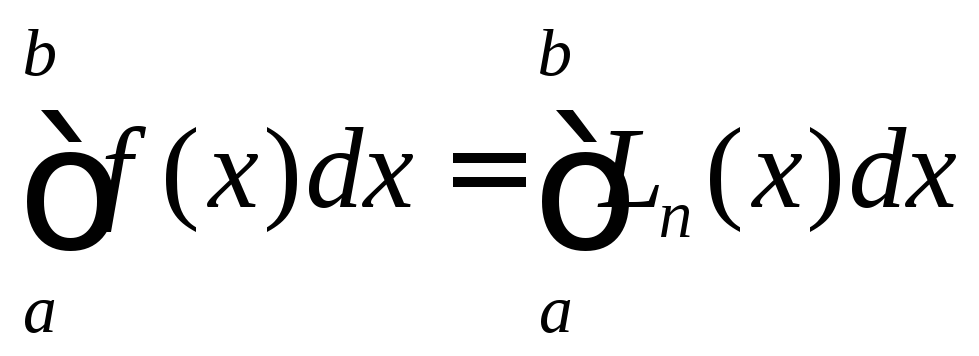(4)

Отсюда следует квадратурная формула 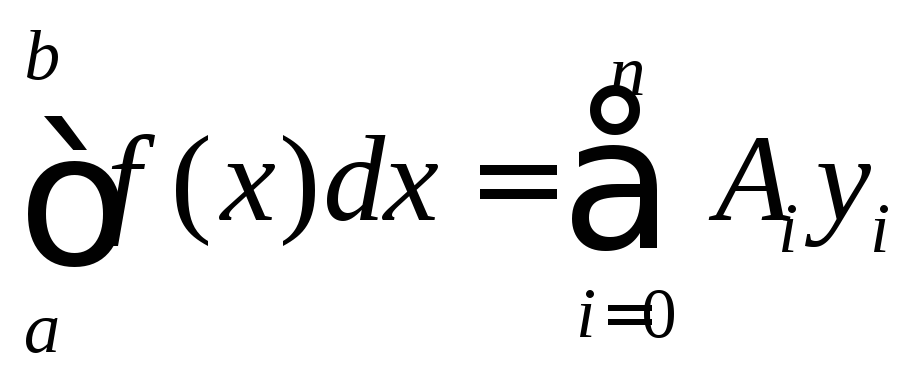, (5)

Где 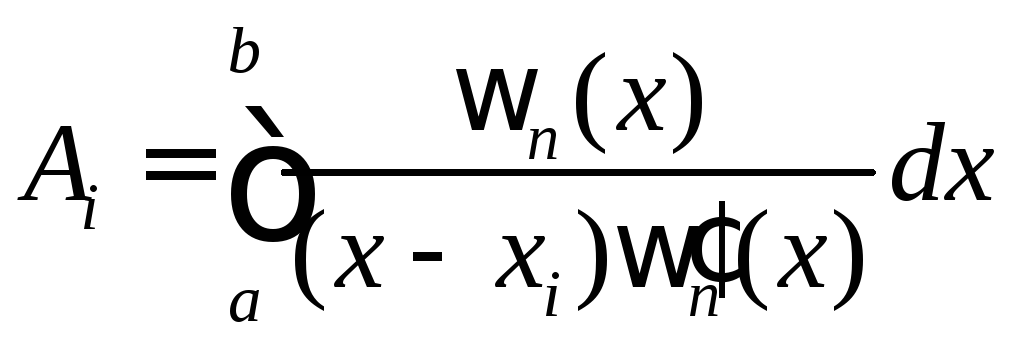,i =0, 1, …,n. (6)

Если пределы интегрирования aиb являются узлами интерполирования, то квадратурная формула (5) называется формулойзамкнутого типа, иначе –открытого.

Тогда

n=0:(7a)

n= 1:,(7b)

n= 2:, , (7c)

…

8. Формулы прямоугольников

Применяя формулу (5) при n=0 с учетом того, что в этом случае, согласно (7а),A₀=b–a, получаем

,

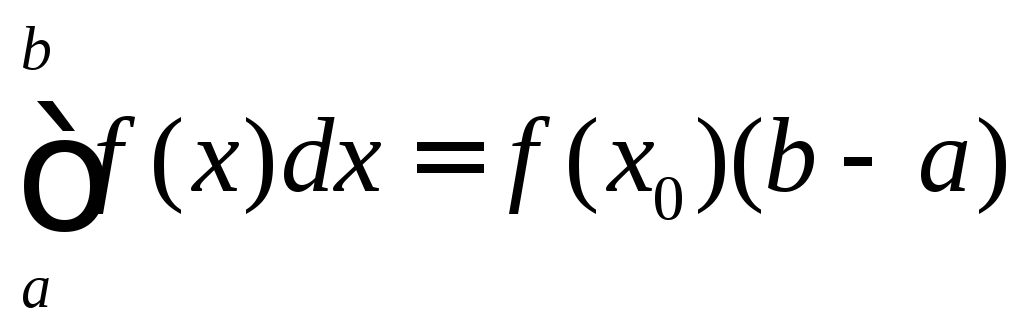где x₀– произвольная точка из отрезка [a,b]. Наиболее часто эта формула применяется, когдаx₀=aилиx₀=b. В первом случае получается формула левых прямоугольников

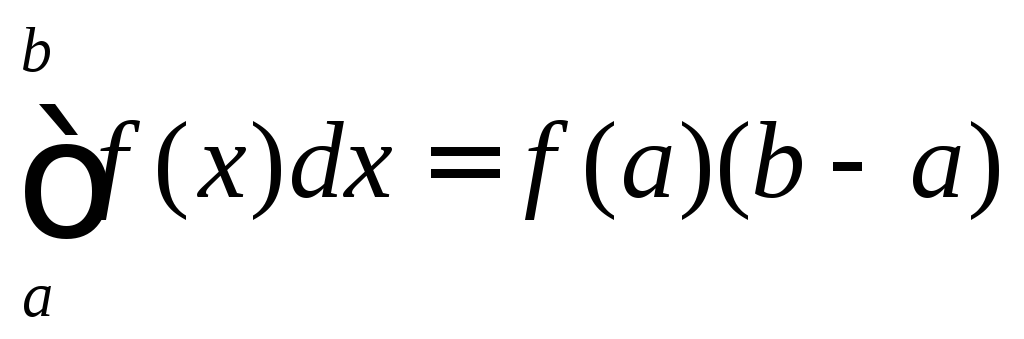
во втором случае – формула правых прямоугольников

При практическом применении формул прямоугольников отрезок интегрирования [a,b] разбивают наmравных частей и, пользуясь тем, что,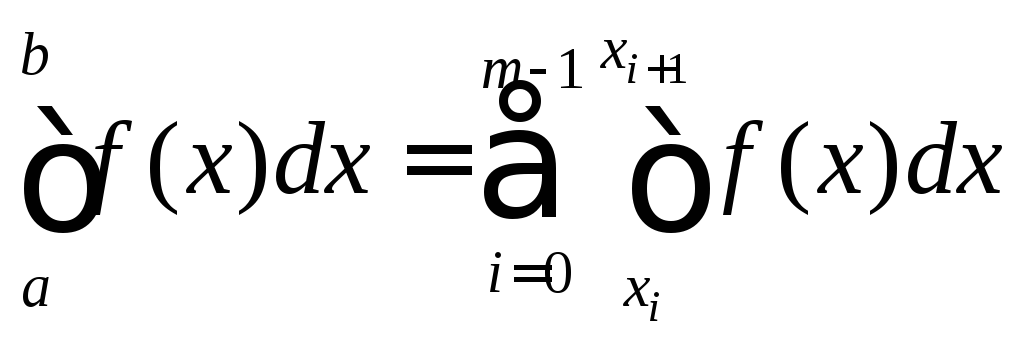

применяют формулы прямоугольников на каждом из отрезков [x_i,x_i+1]. В результате получается обобщенные формулы прямоугольников:

и

.

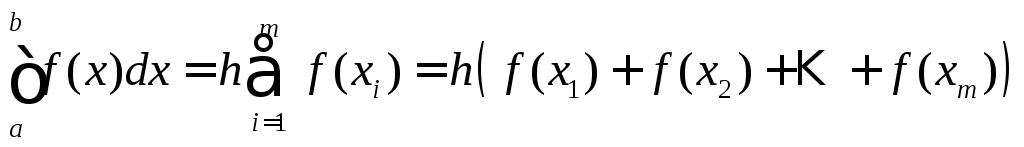9. Формула трапеций

Рассмотрим применение формулы (5) при n=1 тогда, когдаx₀=aиx₁=b. В таком случае получим из (7b)A₀=A₁= (b–a)/2 и формула (5) сведется к следующей

Эта формула называется формулой трапеций. Геометрический смысл формулы трапеций заключается в том, что подынтегральная функция y=f(x) заменяется прямойy= [[f(b)f(a)] / (ba)] (xa), т.е. прямой, соединяющей точки с ординатамиf(a) иf(b). За приближенное значение искомой площади принимается площадь трапеции.

Обобщенная формула трапеций имеет вид:

.

Геометрически это означает, что криволинейная трапеция разбивается на mтрапеций, а криваяy= f(x) заменяется ломаной.

10. Формула Симпсона

Рассмотрим применение формулы (5) при n = 2, когдаx₀=a,x₁=a+h,x₂=a+ 2h=b. В таком случае из (7с) получим

=======,

, ,

Подставляя эти выражения в (5), получим квадратурную формулу Симпсона

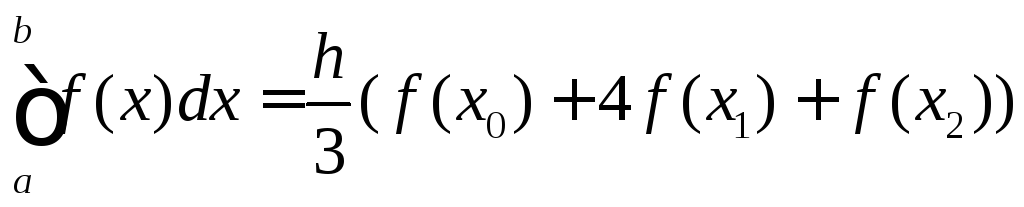
Обобщенная формула Симпсона имеет вид =

=

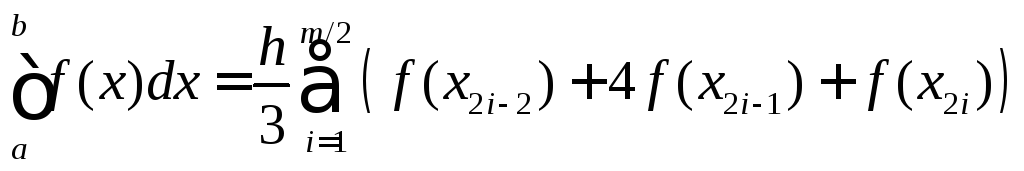В этой формуле число mявляется четным.

Геометрический смысл формулы Симпсона заключается в том, что подынтегральная функция заменяется параболой (полиномом степени n = 2), проведенной через точки с ординатамиf(a),f[(a+b)/2],f(b). Для обобщенной формулы Симпсона подынтегральная функция заменяется набором парабол, проведенных через каждые три соседние точки.

11. Оценка погрешности квадратурных формул

Имеем

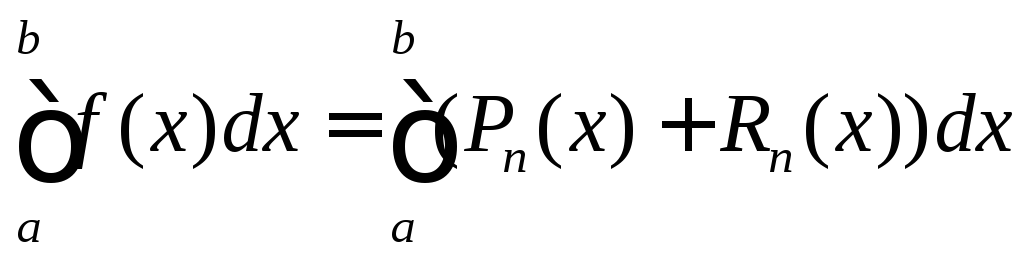
где P_n(x) интерполяционный полином степениn, аR_n– его погрешность. Тогда погрешность соответствующей квадратурной формулы равна.

Явное выражение для погрешности интерполяционного полинома было получено ранее .

Отсюда следует =

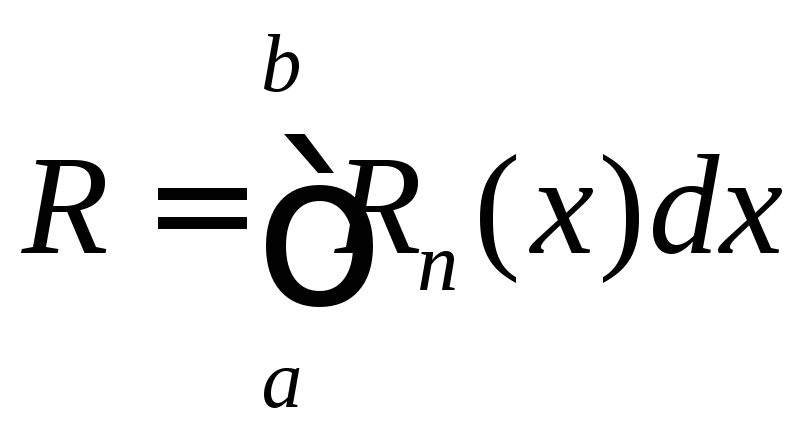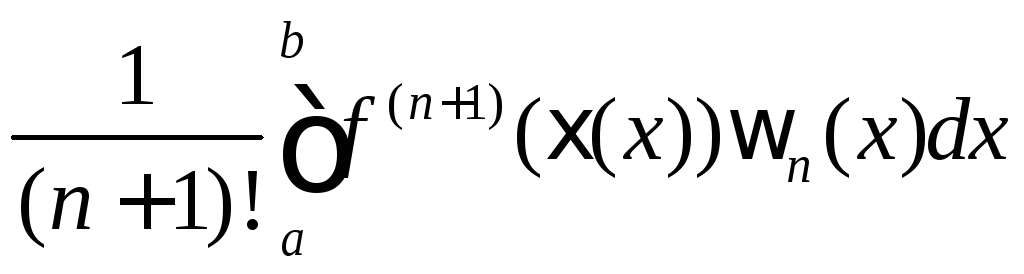
С учетом этого получаются формулы для оценки погрешности Здесь.

12. Оценка погрешности квадратурных формул прямоугольников

Для формулы прямоугольников (n= 0) имеем=

и Здесь.

Для обобщенной формулы прямоугольников имеем следующее выражение оценки погрешности ,

13. Оценка погрешности квадратурной формулы трапеций.

Для формулы трапеций (n= 1) имеем

=

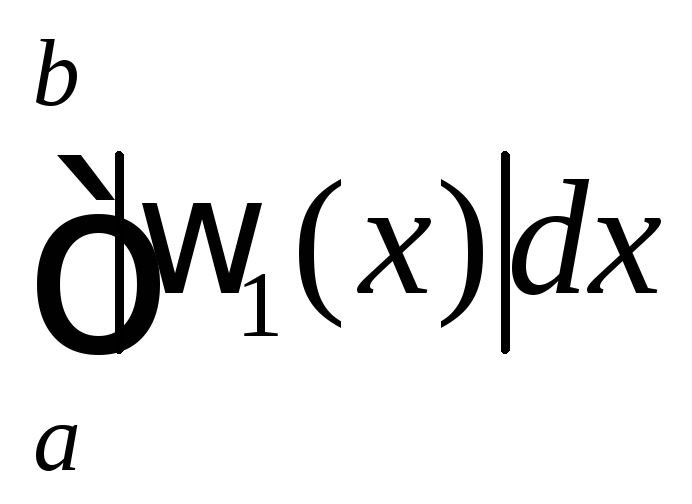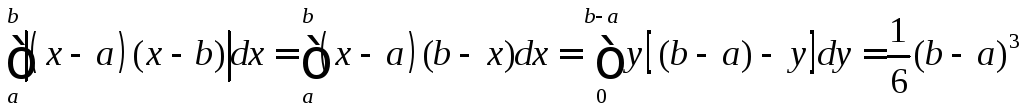
И

Здесь .

для обобщенной формулы трапеций – следующее , (8)

14.Оценка погрешности квадратурной формулы Симпсона.

Для формулы Симпсона (n= 2,x₀=a,x₁=a+h,x₂=a+ 2h=b) имеем

====

Отсюда следует

а для обобщенной формулы Симпсона – следующее (9)

Здесь h– расстояние между равноотстоящими узлами.

Более глубокий анализ показывает, что для обобщенной формулы Симпсона справедлива также и следующая оценка: (9)

15. Численное дифференцирование

Численное дифференцирование применяется, если функцию y=f(x) трудно или невозможно продифференцировать аналитически – например, если она задана таблично. Численное дифференцирование используется также при решении дифференциальных уравнений разностными методами.

При численном дифференцировании функцию f(x), заданную на отрезке [a, b], аппроксимируют на этом отрезке легко вычисляемой функцией φ(x) и полагают, что. При этом можно использовать различные способы аппроксимации. Рассмотрим аппроксимацию интерполяционным полиномом Ньютона.

Пусть на отрезке [a, b] известноn+1 значениеy_i^* =f(x_i^*) функцииf(x) в точкахx=x_i^*,i= 0, 1, …,n,x₀^*=a,x_n^*=b,x_i+1^*=x_i^*+hи пусть требуется приближенно определитьk-ю производнуюf^(k)(x) в некоторой точкеxотрезка [a, b], такой, чтоx_I^*xx_I+1^*, где 0In1.

Выберем среди множества {x_i^*}m+1 последовательно расположенных узловx_R^*,x_R+1^*,x_R+2^*, …,x_R+m^*, таких, чтоx_R^*xx_R+m^*. Введя обозначенияx₀=x_R^*,x₁=x_R+1^*,x₂=x_R+2^*, …,x_m=x_R+m^*,t_i=xx_i,y_i =f(x_i),i = 0, 1, …,m, запишем полином Ньютона степениm:

= =

=

При аппроксимации интерполяционным полиномом Ньютона полагается (1)

Здесь

…

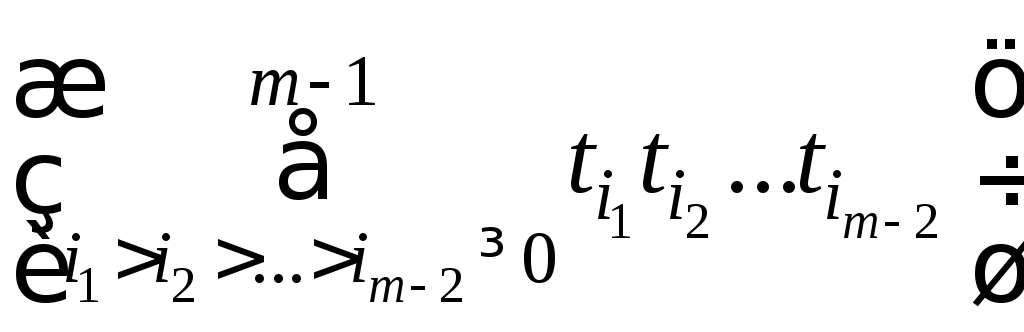
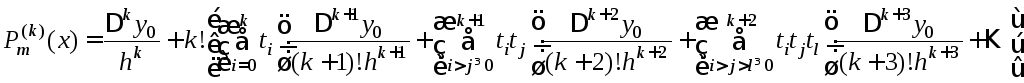
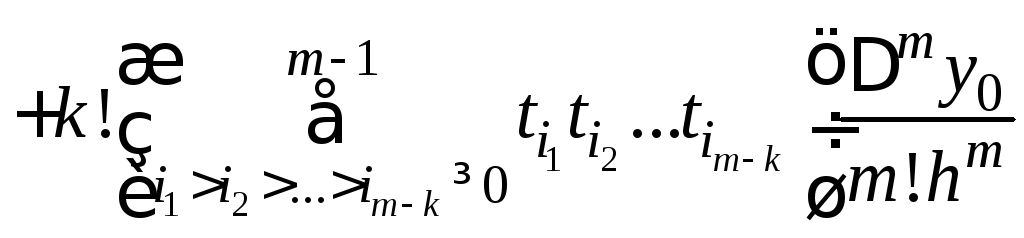
В этой сумме mk+1 слагаемых.