
- •Введение
- •I. Методические указания к ответам на теоретические вопросы
- •§1. Этапы научного исследования. Роль и место вычислительного эксперимента и численных методов
- •§2. Основные понятия теории погрешностей. Общая формула вычисления погрешности
- •§3. Метод Ньютона решения алгебраических и трансцендентных уравнений
- •§4. Решение систем линейных алгебраических уравнений.
- •§5. Метод Гаусса решения систем линейных алгебраических уравнений и его модификации
- •§6. Метод простой итерации решения систем линейных алгебраических уравнений
- •§7. Алгебраическое интерполирование. Исследование существования и единственности интерполяционного полинома
- •§8. Интерполяционный полином Лагранжа.
- •§9. Численное интерполирование. Полином Ньютона
- •§10. Численное интегрирование. Формулы Ньютона-Котеса. Оценка погрешности квадратурных формул
- •§11. Классификация и общая характеристика методов решения дифференциальных уравнений. Хорошо и плохо обусловленные задачи
- •§12. Метод Эйлера. Алгоритм и оценка погрешности
- •§13. Метод Рунге-Кутта. Алгоритм и оценка погрешности
- •§14. Численные методы решения краевых задач для обыкновенных дифференциальных уравнений
- •§15. Идея метода сеток решения уравнений в частных производных
- •§16. Аппроксимация дифференциального уравнения разностным и ее порядок. Устойчивость. Сходимость
- •§17. Метод сеток решения краевых задач для дифференциальных уравнений эллиптического типа
- •II. Методические указания к решению задач
- •Список рекомендуемой литературы
§6. Метод простой итерации решения систем линейных алгебраических уравнений
При изложении ответа на этот вопрос следует записать систему линейных алгебраических уравнений, привести ее к виду, удобному для построения итерационного процесса, записать алгоритм (вычислительную схему) метода простой итерации, доказать теорему о достаточном условии сходимости и получить оценку приближения. Кроме того, необходимо знать определение канонической нормы и уметь привести примеры норм.
Дана система линейных алгебраических уравнений
![]() .
(11)
.
(11)
Здесь матрица A – заданная квадратная неособенная матрица, так что система (11) имеет единственное решение, b – заданный вектор (правая часть), x – искомый вектор. Эквивалентными преобразованиями приведем систему (11) к виду x=αx+β, (12)
где α – матрица той же размерности, что и А, а β – вектор, так что решение системы (11) является решением системы (12) и, наоборот, решение системы (12) является решением системы (11).
Выберем некоторый начальный вектор x0 и построим итерационный процесс, который называется методом простой итерации
xk+1= αxk+β, k=0, 1, … (13)
Достаточное
условие сходимости метода простой
итерации дает следующая теорема:
Процесс итерации (13) для приведенной
системы (12) сходится к ее единственному
решению, если какая-нибудь каноническая
норма матрицы α меньше 1:
![]() .
.
Условие
завершения вычислений выводится с
помощью оценки погрешности
k-го
приближения xk,
которая имеет вид:
![]()
Поэтому
для получения решения xk
системы (12) с точностью ε вычисления
следует продолжать до выполнения условия
![]() .
.
§7. Алгебраическое интерполирование. Исследование существования и единственности интерполяционного полинома
При
изложении ответа на этот вопрос следует
дать математическую постановку задачи
интерполирования, определения
интерполяционной функции, узлов
интерполяции, алгебраического
интерполирования, показать линейную
независимость степенных функций
![]() ,
доказать
единственность
интерполяционного полинома для данной
таблицы значений функции.
,
доказать
единственность
интерполяционного полинома для данной
таблицы значений функции.
Математическая
постановка задачи интерполирования
заключается в следующем. Пусть R
- пространство действительных функций,
определенных на отрезке [a,b],
и {φi}
- заданная конечная или счетная система
функций из R,
такая, что их любая конечная подсистема
является линейно-независимой. Для данной
конечной совокупности точек
![]() (xi≠xj
при i≠j),
принадлежащих отрезку [a,b],
и данной функции f(x)
из R
найти функцию φ, являющуюся линейной
комбинацией функций {φi},
так, чтобы в заданных точках значения
f
и φ совпадали.
Другими словами, определить константы
(xi≠xj
при i≠j),
принадлежащих отрезку [a,b],
и данной функции f(x)
из R
найти функцию φ, являющуюся линейной
комбинацией функций {φi},
так, чтобы в заданных точках значения
f
и φ совпадали.
Другими словами, определить константы
![]() так, чтобы
так, чтобы
![]() .
(14)
.
(14)
Функция
![]() называется интерполирующей
функцией,
а точки
- узлами
интерполяции.
называется интерполирующей
функцией,
а точки
- узлами
интерполяции.
Если {φi} являются степенями , то говорят об алгебраической интерполяции, а функцию φ(x) называют интерполяционным полиномом. При m=n для любого набора значений f(xj) можно построить интерполяционный полином степени n и притом только один. Действительно, в этом случае определитель системы линейных алгебраических уравнений (14)
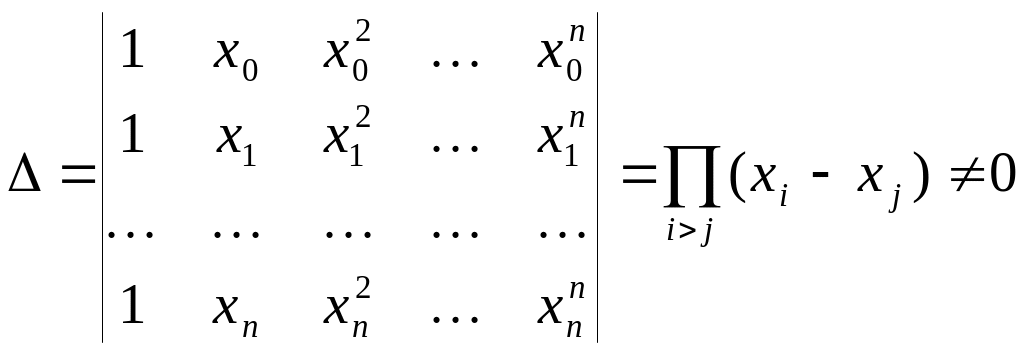
является определителем Вандермонда и отличен от нуля, так как среди узлов интерполяции нет двух совпадающих. Следовательно, решение системы (14) существует, единственно и коэффициенты интерполяционного полинома определяются однозначно.
