3. Фазовий об’єм у  - просторі.

В СФ принципово важливою є така характеристика системи як фазовий об’єм класичної системи. Обчислимо цей об’єм для ідеального газу.

Об’єм фазового простору однієї частинки, яка вільно рухається в об’ємі V фізичного простору і має енергію в інтервалі від 0 до , дорівнює

(5)

Координати x, y, z обмежені розмірами посудини, в якій знаходиться газ. Положення частинки ніяк не зв’язано з її імпульсом, тому інтегрувати можна незалежно

.

Оскільки , то якщо імпульс частинки p знаходиться в межах

, де .

Можливі будь-які напрямки руху, тому

.

Однак в будь-який момент

Звідси видно, що всі допустимі мікростани частинки заповнюють у підпросторі імпульсів - простору сферу радіусом . Її об’єм дорівнює

Для фазового об’єму одержуємо

(6)

Звідси випливає, що мікростанам з енергіями від до відповідає елементарний об’єм - простору.

(7)

Фазовий об’єм ідеального газу

Нехай в посудині об’ємом V знаходиться ідеальний газ, який складається з N однакових частинок. Знайдемо фазовий об’єм цієї системи якщо її енергія може набувати значень в межах від 0 до E.

Кожна частинка може знаходитись в будь-якій точці об’єму V і мати будь-який напрямок руху (молекулярний хаос). Взаємодія при зіткненнях між частинками викликає зміну їх енергії, але всі допустимі значення енергії однієї частинки лежать в межах від 0 до E.

Внаслідок незалежності координат і імпульсів частинок фазовий об’єм системи

(8)

Координати всіх частинок змінюються незалежно в межах об’єму V, який займає газ. Тому

Енергія системи дорівнює сумі кінетичних енергій частинок. При цьому повинна виконуватись нерівність

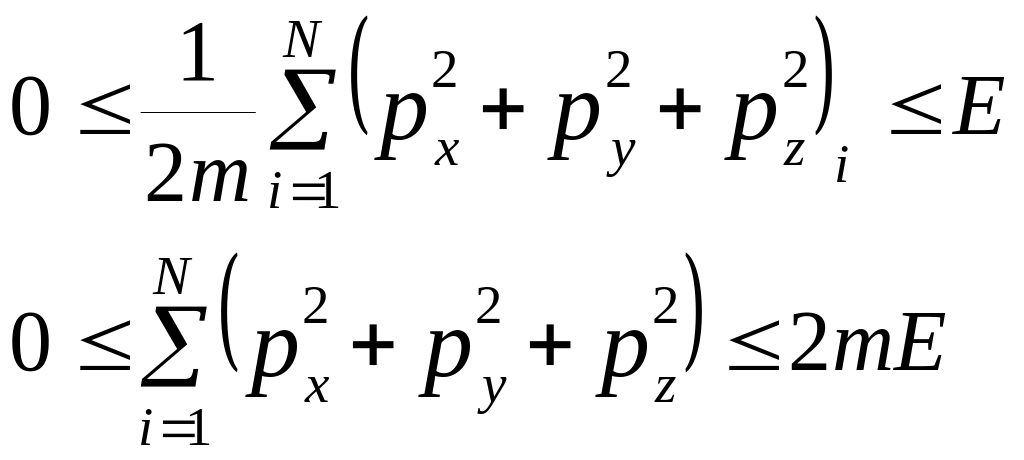або (9)

Кожна з проекцій імпульсу може мати значення в межах від до . Отже нерівність (9) виділяє у просторі імпульсів сферу радіусом з центром у початку координат. Інтеграл по імпульсах рівний об’єму цієї сфери.

З міркувань розмірності об’єм 3N - вимірної кулі повинен бути пропорційним .

Тоді одержимо

(10)

де Д_N - сталий множник (коефіцієнт пропорційності), який не залежить від енергії і об’єму системи.

Елементарний об’єм, що припадає на інтервал енергії системи

(11)

3. Задання мікростану квантової системи.

Згідно квантової механіки координати p і q не можуть бути визначені одночасно (принцип невизначеності Гейзенберга) тому класичне розуміння фазового простору втрачає свій зміст. В квантовій статистичній фізиці мікроскопічні стани системи визначаються як стани у квантовомеханічному розумінні. Ці мікро стани описуються хвильовими функціями , які разом з допустимими значеннями енергії знаходяться з рівняння Шредінгера

(12)

де - гамільтоніан системи.

Таким чином, мікроскопічні стани системи з точки зору квантової статистичної фізики це сукупність дискретних квантових станів.

Хвильові функції залежать від координат всіх частинок. Для цілей статистичної фізики знати хвильові функції не обов’язково : досить знати рівні енергії , кратність їх виродження та квантові числа в які повністю визначають стан системи.

Рівняння (11) можна розв’язати лише наближено. Виключенням є ідеальний газ, в якому взаємодією між частинками можна знехтувати. В такому випадку хвильову функцію системи можна представити як добуток хвильових функцій окремих частинок a рівняння ( ) “розпадається” на сукупність рівнянь Шредінгера для окремих частинок (одночастинкових рівнянь).

Розглянемо ідеальний газ, молекули якого вільно рухаються в посудині кубічної форми з ребром a. Всі молекули знаходяться в однакових умовах і тому розв’язавши одне з одночастинкових рівнянь знайдемо всі стани, в яких може знаходитись будь-яка молекула. Як відомо з квантової механіки, стани молекул за умов розглядуваної задачі визначаються трійкою квантових чисел що незалежно набувають знань, рівних числам натурального ряду.

Енергія i – тої молекул рівна

(13)

Очевидно .