
- •Основний постулат і основна ідея статистичної фізики
- •Розподіл Максвела – приклад статистичного розподілу.
- •Фізичний зміст параметрів розподілу Максвела.
- •Тепер запишемо вирази для густини імовірності
- •Властивості і застосування максвелівського розподілу. Розподіл компонента швидкості
- •Розподіл Больцмана.
- •Мікроскопічний опис макроскопічних систем
- •Мікроскопічний опис класичної системи.
- •Фазовий простір.
- •Фазовий об’єм у - просторі.
- •Фазовий об’єм ідеального газу
- •Внаслідок незалежності координат і імпульсів частинок фазовий об’єм системи
- •Задання мікростану квантової системи.
- •Енергія всього газу системи
- •Розрахунок числа можливих станів для ідеального газу.
- •Співвідношення невизначеностей і число квантових станів.
- •Закони статистичного розподілу для систем багатьох частинок
- •Залежність функції розподілу від енергії системи.
- •2. Мікроканонічний розподіл.
- •Канонічний розподіл Гіббса.
- •Великий канонічний розподіл Гіббса.
- •Квантові статистики.
- •06601, Київ-30, вул. Пирогова, 9.
Розподіл Максвела – приклад статистичного розподілу.
Перший крок у розробці загальних методів обчислення статистичних середніх зробив у 1959 році Джемс Максвел, ввівши до фізики поняття імовірності.
Максвел поставив таке завдання: визначити середнє число частинок, швидкості яких лежать в заданих межах, після великого числа зіткнень між великою кількістю частинок. Він розв’язав цю задачу, але головною його заслугою була постановка нової проблеми.
Розглянемо задачу Максвела для ідеального газу, що знаходиться в стані термодинамічної рівноваги. Припустимо, що молекули рівномірно розподілені в просторі (в посудині, де вони знаходяться) а їх швидкості рівномірно розподілені за всіма напрямками (припущення про молекулярний хаос).
Встановлення молекулярного хаосу зумовлено взаємодією між молекулами.
Зважаючи
на рівномірний розподіл молекул у
просторі, надалі розглядатимемо лише
тривимірний “простір швидкостей”, у
якому кожна точка відповідає молекулі
з строго заданою швидкістю
![]() о має компоненти
о має компоненти
vx; vy; vz.
|
![]() ,
,
де
![]() - густина імовірності для vx.
В силу ізотропності простору швидкостей
функції густини імовірностей (функціональні
залежності) для vy
і vz
будуть такі ж.
- густина імовірності для vx.
В силу ізотропності простору швидкостей
функції густини імовірностей (функціональні
залежності) для vy
і vz
будуть такі ж.
Імовірність того, що кінець радіуса-вектора компонентами якого є vx; vy; vz, знаходиться в елементарному паралелепіпеді з сторонами dvx; dvy; dvz в околі точки з координатами (vx; vy; vz) можна представити так
|
(1) |
де
![]() ,
,
![]() - густина імовірності того, що швидкість
має абсолютну величну
- густина імовірності того, що швидкість
має абсолютну величну
![]() з компонентами vx;
vy
і vz,
а не якимись іншими.
з компонентами vx;
vy
і vz,
а не якимись іншими.
З припущення про молекулярний хаос випливає незалежність значень компонентів швидкості, а отже і незалежність їх імовірностей. В зв’язку з цим імовірність (1) можна також записати так (за теоремою про множення імовірностей незалежних подій)
|
(2) |
Порівняння (1) і (2) дає
|
(3) |
Для
того, щоб з цього функціонального
рівняння визначити функції
![]() і
і
![]() ,
зробимо так:
,
зробимо так:
а) прологарифмуємо вираз (3)
|
(4) |
б) знайдемо похідну від (4) по vx
|
(5) |
в) введемо позначення
![]()
тоді (5) матиме вигляд:
|
(6) |
г) диференціюючи (6) по vy або vz, одержуємо
![]()
Приймемо, що
![]() ,
де
,
де
![]() - суть додатна величина, множник 2
приєднаємо для зручності, а знак мінус
потрібен для того, щоб виконувалась
умова нормування.
- суть додатна величина, множник 2
приєднаємо для зручності, а знак мінус
потрібен для того, щоб виконувалась
умова нормування.
Тоді,
в силу (6),
![]() або
або
|
(7) |
де
![]() .
.
Таким чином, з умови ізотропності і умови незалежності руху вздовж взаємно перпендикулярних осей випливає, що імовірність того, що, компонент швидкості vx знаходиться в інтервалі від vx до vx+dvx, визначається співвідношенням
![]() ,
,
де С і - деякі параметри (сталі), які повинні бути визначені за допомогою додаткових умов.


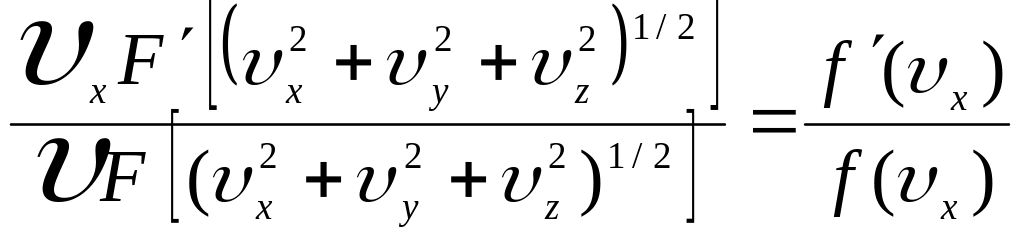 ,
,