
- •Основний постулат і основна ідея статистичної фізики
- •Розподіл Максвела – приклад статистичного розподілу.
- •Фізичний зміст параметрів розподілу Максвела.
- •Тепер запишемо вирази для густини імовірності
- •Властивості і застосування максвелівського розподілу. Розподіл компонента швидкості
- •Розподіл Больцмана.
- •Мікроскопічний опис макроскопічних систем
- •Мікроскопічний опис класичної системи.
- •Фазовий простір.
- •Фазовий об’єм у - просторі.
- •Фазовий об’єм ідеального газу
- •Внаслідок незалежності координат і імпульсів частинок фазовий об’єм системи
- •Задання мікростану квантової системи.
- •Енергія всього газу системи
- •Розрахунок числа можливих станів для ідеального газу.
- •Співвідношення невизначеностей і число квантових станів.
- •Закони статистичного розподілу для систем багатьох частинок
- •Залежність функції розподілу від енергії системи.
- •2. Мікроканонічний розподіл.
- •Канонічний розподіл Гіббса.
- •Великий канонічний розподіл Гіббса.
- •Квантові статистики.
- •06601, Київ-30, вул. Пирогова, 9.
Канонічний розподіл Гіббса.
Для розв’язання конкретних задач зручніше розглядати не енергетично ізольовані системи, а системи, які знаходяться в тепловому контакті з оточуючим середовищем, температура якого стала (з термостатом), або розглядати системи, які можуть обмінюватись з термостатом енергією і частинками.
Розглянемо
замкнену систему з жорсткими стінками
(N=const,
V=const),
яка обмінюється енергією з термостатом
і разом з ним утворює велику квантову
ізольовану систему. Енергія системи не
має строго фіксованого значення.
Статистичний ансамбль у такому випадку
називається канонічним. Поставимо
питання про те, яка імовірність знайти
нашу систему в станах з енергією між
![]()
![]() .
.
Енергії великої системи, термостата і системи пов’язані співвідношенням
![]() (9)
(9)
де
![]() - енергія термостата в k-тому
стані;
- енергія термостата в k-тому
стані;
![]() - енергія системи в і-тому
стані; знак “
- енергія системи в і-тому
стані; знак “![]() ”
підкреслює той факт, що енергія великої
системи незмінна, а енергією взаємодії
ми нехтуємо.
Останнє означає, що систему і термостат
можна вважати незалежними протягом
тривалого часу. Квазінезалежна система
може знаходитися у будь-якому із станів
з енергією
,
а термостат – у станах з енергією
.
Зміна мікростану системи при незмінній
енергії не впливає на стан термостата
і навпаки.
”
підкреслює той факт, що енергія великої
системи незмінна, а енергією взаємодії
ми нехтуємо.
Останнє означає, що систему і термостат
можна вважати незалежними протягом
тривалого часу. Квазінезалежна система
може знаходитися у будь-якому із станів
з енергією
,
а термостат – у станах з енергією
.
Зміна мікростану системи при незмінній
енергії не впливає на стан термостата
і навпаки.
Кожному
інтервалу енергії великої системи,
термостату і системи відповідає певне
число квантових станів. Наприклад, число
доступних квантових станів, які
відповідають енергії системи в межах
від
до
![]() будемо позначати
будемо позначати
![]() .
Як ми уже раніше з’ясували,
.
Як ми уже раніше з’ясували,
![]() ~
.
З цього випливає така властивість
:
якщо
є система, що складається з двох незалежних
частин, і число станів кожної з них рівне
~
.
З цього випливає така властивість
:
якщо
є система, що складається з двох незалежних
частин, і число станів кожної з них рівне
![]() і
і
![]() ,
то число станів складної системи рівне
,
то число станів складної системи рівне
![]()
![]() .
.
Наша
велика система знаходиться в стані
рівноваги (за умовою). Отже, до неї можна
застосувати постулат про мікроканонічний
розподіл. З цього постулату випливає,
що імовірність знаходження великої
системи в будь-якому з доступних станів
одна і та ж і рівна 1/![]() .
Нас цікавить імовірність того, що система
знаходиться в станах з енергією
(від
до
).
Ці стани мають місце тоді лише, коли
енергія великої системи не просто
дорівнює Е,
а ще й енергія термостату має певне
значення:
.
Нас цікавить імовірність того, що система
знаходиться в станах з енергією
(від
до
).
Ці стани мають місце тоді лише, коли
енергія великої системи не просто
дорівнює Е,
а ще й енергія термостату має певне
значення:
![]() .
Тому шукана може бути одержана сумуванням
1/
по всіх станах, для яких енергія системи
, а енергія термостату
:
.
Тому шукана може бути одержана сумуванням
1/
по всіх станах, для яких енергія системи
, а енергія термостату
:
![]() ,
,
де const – не залежить від .
Певне число доступних станів великої системи, в яких енергія квазінезалежної системи рівна , виражається добутком
![]() .
.
Отже, шукану імовірність можна представити так
![]() (10)
(10)
Для
того, щоб розподіл (10) набув конкретного
вигляду, необхідно розкрити залежність
![]() від
.
Це можна зробити, розклавши
від
.
Це можна зробити, розклавши
![]() в ряд Тейлора і обмежившись першим
членом розкладу. Перш ніж це робити,
представимо число станів так:
в ряд Тейлора і обмежившись першим
членом розкладу. Перш ніж це робити,
представимо число станів так:
![]()
![]() ,
(11)
,
(11)
де
![]() - нова функція (
- нова функція (![]() ).
).
Розкладемо в ряд Тейлора:
![]() ,
,
де
![]()
Підставляючи, одержимо:
![]() ,
(12)
,
(12)
де
під const
розуміємо
добуток коефіцієнта пропорційності і
величини
![]() , яка не залежить від
і властивостей квазінезалежної системи.
Ця стала може бути знайдена з умови
нормування:
, яка не залежить від
і властивостей квазінезалежної системи.
Ця стала може бути знайдена з умови
нормування:
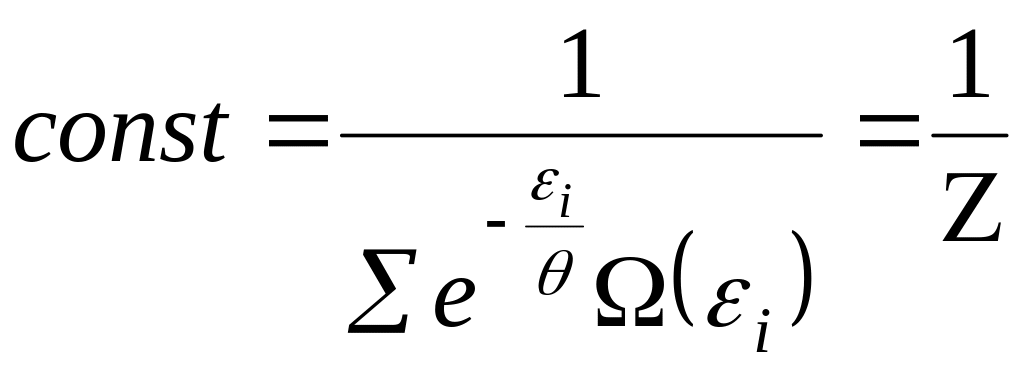
Остаточно одержимо
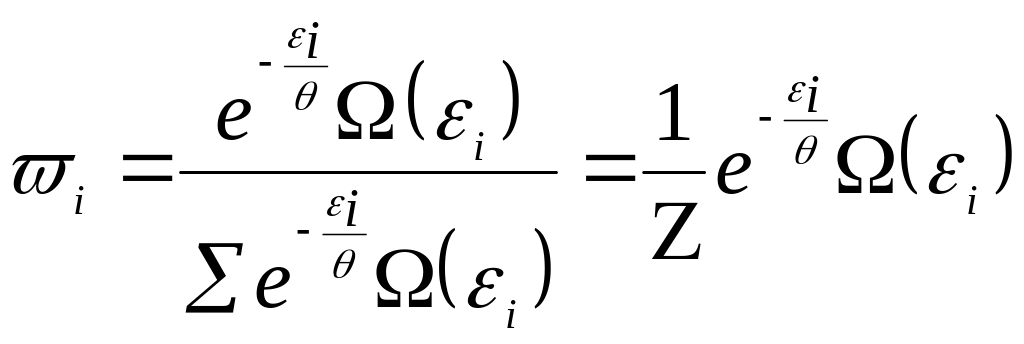 (13)
(13)
Величина
![]() одержала назву модуля розподілу або
статистичної температури. Сума
одержала назву модуля розподілу або
статистичної температури. Сума
![]() називається “статистичною сумою” або
“сумою за станами”.
називається “статистичною сумою” або
“сумою за станами”.
Зауважимо, що ми одержали канонічний розподіл Гіббса з мікроканонічного розподілу для великої системи.
Для класичної квазінезалежної системи канонічний розподіл має такий вигляд
![]() .
(14)
.
(14)
Статистичний інтеграл визначається з умови нормування
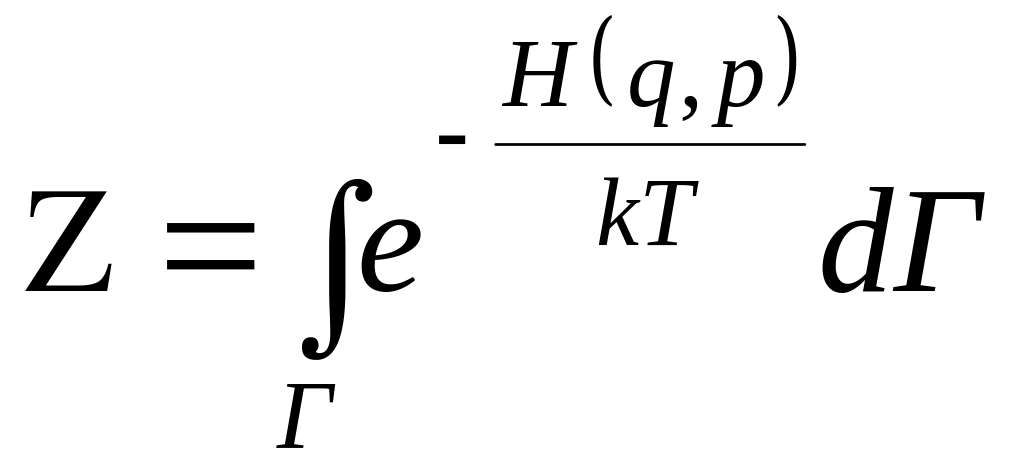 .
.
Статистичний інтеграл пов’язаний з вільною енергією системи:
![]() .
.
Тоді канонічний розподіл Гіббса набуває вигляд
![]() (15)
(15)
