
- •Задачи линейного программирования
- •Постановка задачи
- •Задачи для решения
- •1.2. Свойства решений задач линейного программирования
- •Графический метод решения задач линейного программирования Случай двух переменных
- •Случай многих переменных
- •1.4.2.Симплексный метод
- •Этап 1. Определение начального опорного плана.
- •Случай вырождения
- •Задачи для решения
- •Метод искусственного базиса
- •Задачи для решения
- •1.5. Теория двойственности в линейном программировании
- •1.5.1. Постановка задачи
- •Некоторые частные случаи
- •1.5.2. Основные теоремы двойственности
- •Задачи для решения
- •1.5.3. Геометрическая интерпретация двойственных задач
- •1.5.4. Двойственный симплекс – метод
- •Этап 1. Определение начального опорного плана (псевдоплана).
- •Этап 2. Определение оптимального плана.
- •Задачи для решения
- •1.6. Экономическая интерпретация двойственности
- •1.6.1. Анализ моделей на чувствительность.
- •Использование графического метода.
- •Использование симплекс-метода.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Применение компьютера Инструкция по использованию надстройки «Поиск решения»
- •1.10. Решение задачи с использованием
Задачи для решения
4. Найти решение задач методом искусственного базиса.
4.15.
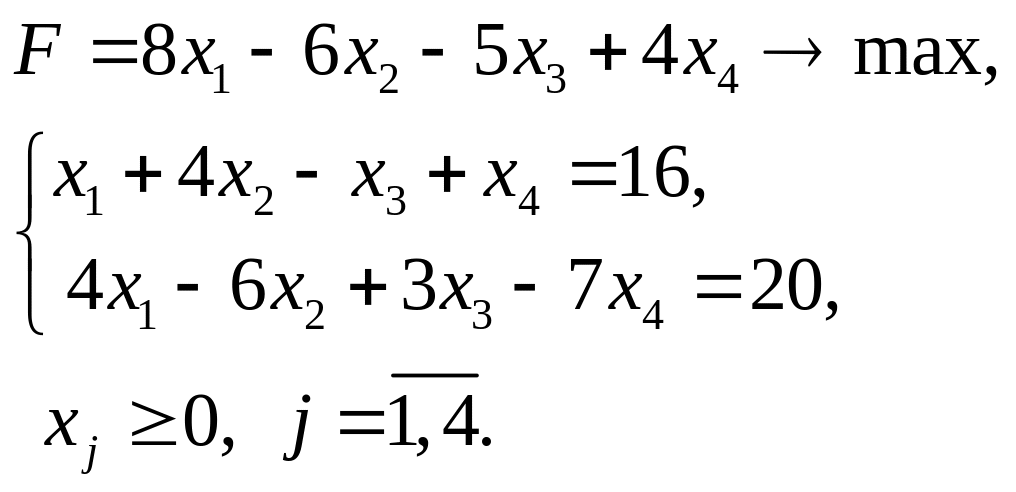
4.16.

4.17.
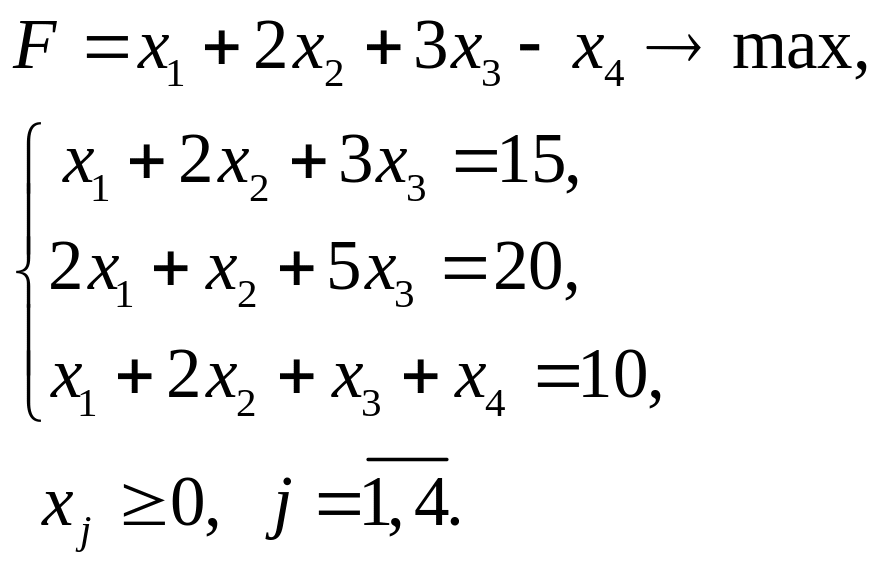
4.18.
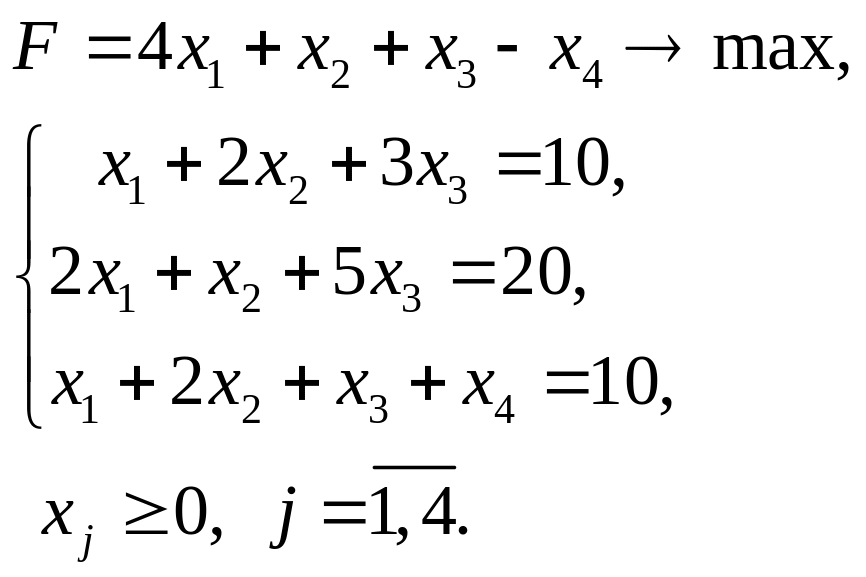
4.19.
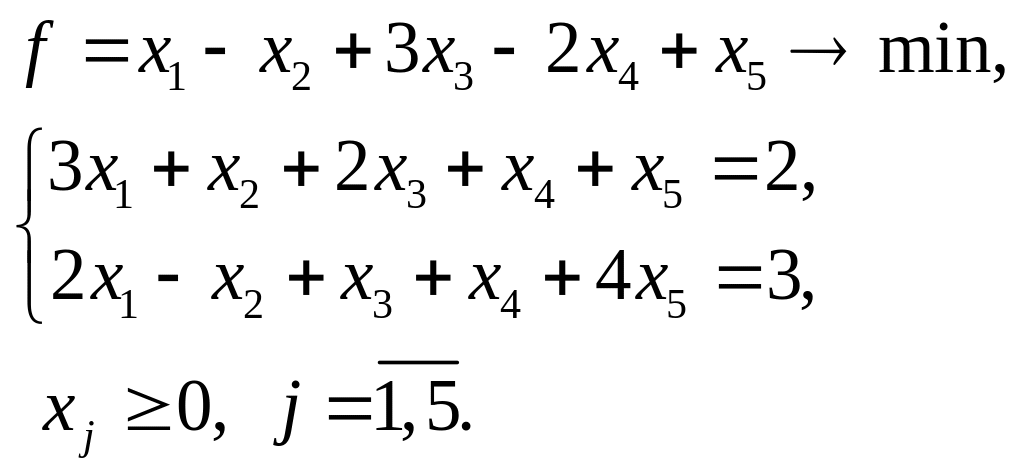
4.20.
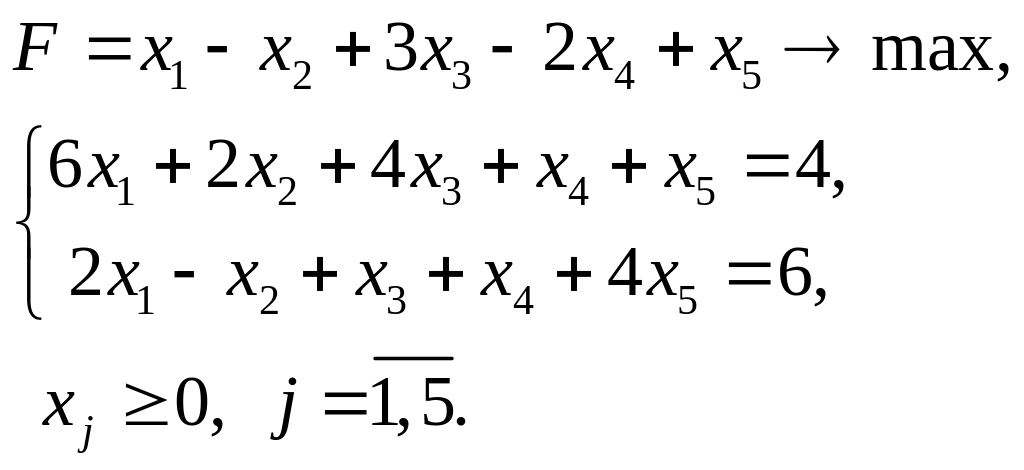
4.21.
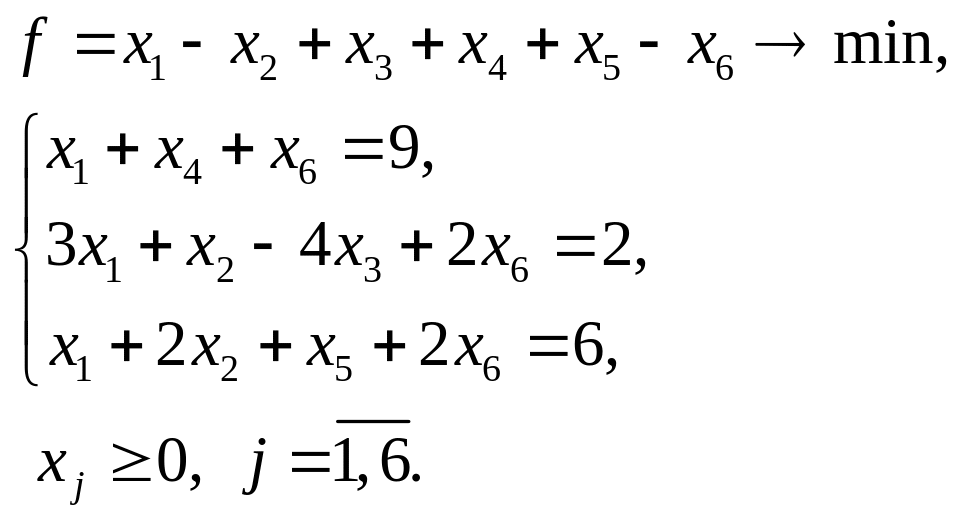
4.22.
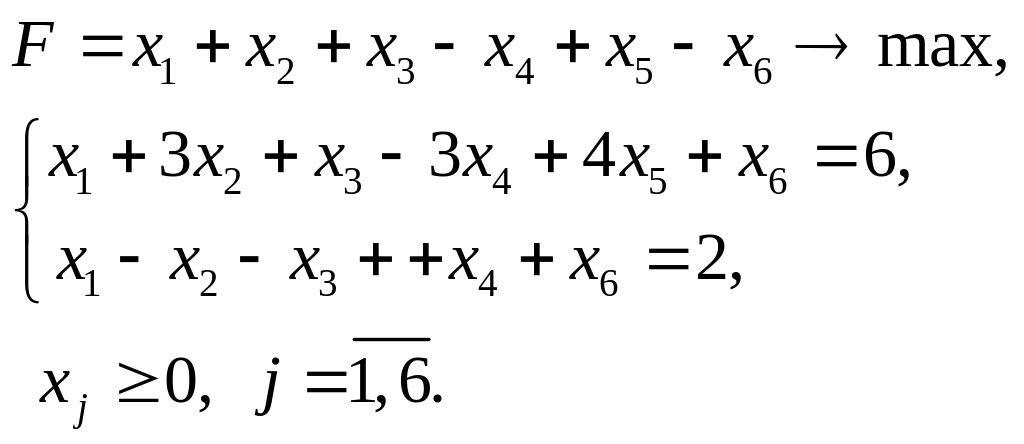
1.5. Теория двойственности в линейном программировании
1.5.1. Постановка задачи
Пусть исходная задача линейного программирования записывается в виде:
(1.16)
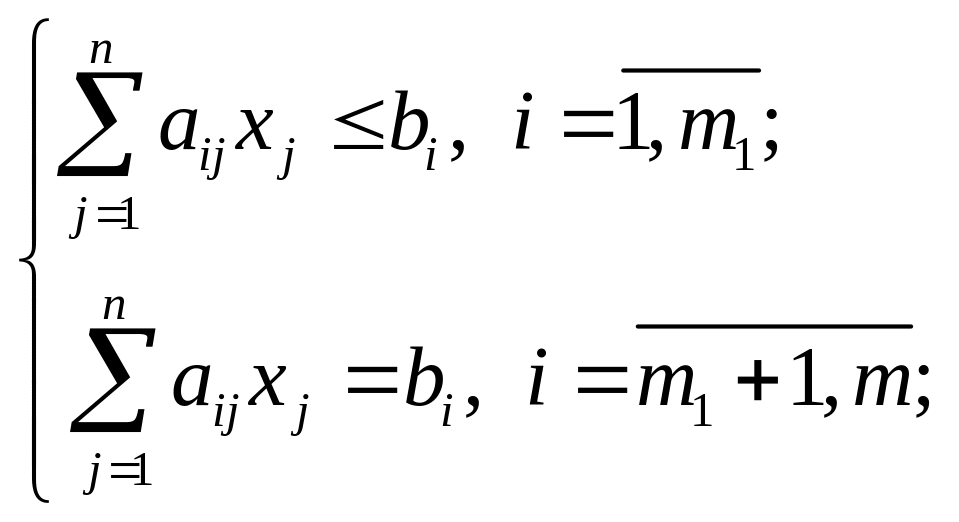 (1.17)
(1.17)
(1.18)
Двойственная к ней задача будет иметь вид:
![]() (1.19)
(1.19)
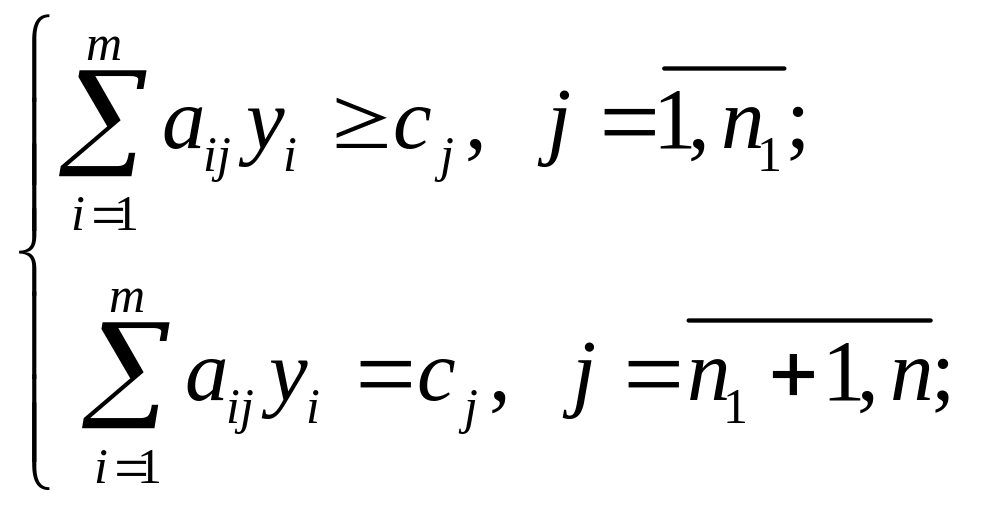 (1.20)
(1.20)
![]() (1.21)
(1.21)
В матричной форме формулировка задачи будет следующей.
Для прямой задачи:
![]() (1.16*)
(1.16*)
![]() (1.17*)
(1.17*)
(1.18*)
Для двойственной –
![]() (1.19*)
(1.19*)
![]() (1.20*)
(1.20*)
![]() (1.21*)
(1.21*)
При записи двойственной задачи действуют следующие правила.
Если прямая (исходная) задача решается на максимум (1.16) – (1.18), то двойственная к ней (1.19) – (1.21) – на минимум и наоборот.
Коэффициенты целевой функции прямой задачи становятся свободными членами для ограничений двойственной задачи.
свободные члены прямой задачи
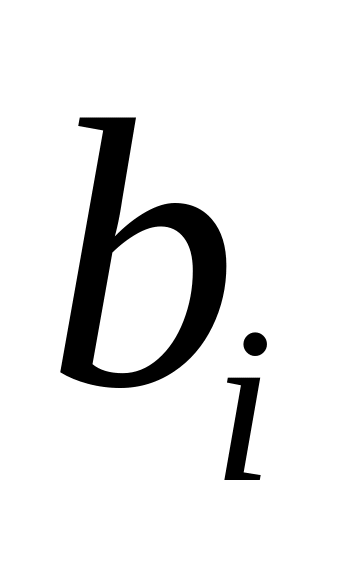 становятся коэффициентами двойственной
целевой функции.
становятся коэффициентами двойственной
целевой функции.Матрица ограничений двойственной задачи является транспонированной по отношению к матрице ограничений прямой задачи.
Если прямая задача решается на максимум, то её система ограничений имеет в неравенствах знак « » или « = ». Двойственная ей задача решается на минимум, и её система ограничений имеет вид неравенств типа « » или « = ».
Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной – числу переменных прямой.
Если прямая задача задана в симметричной форме с n переменными и при приведении её к канонической форме были добавлены ещё m переменных, то между переменными
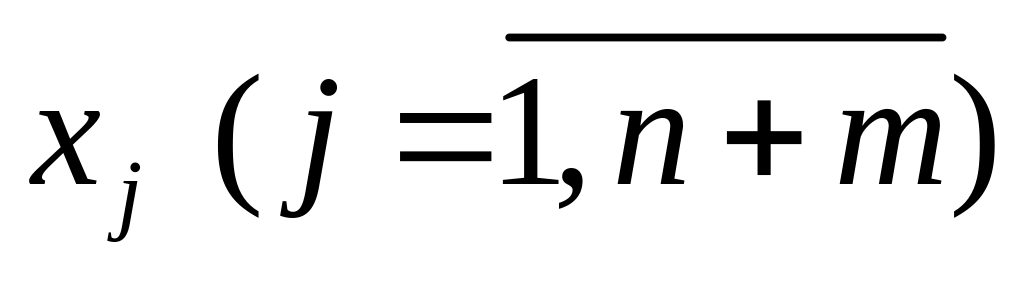 и
и
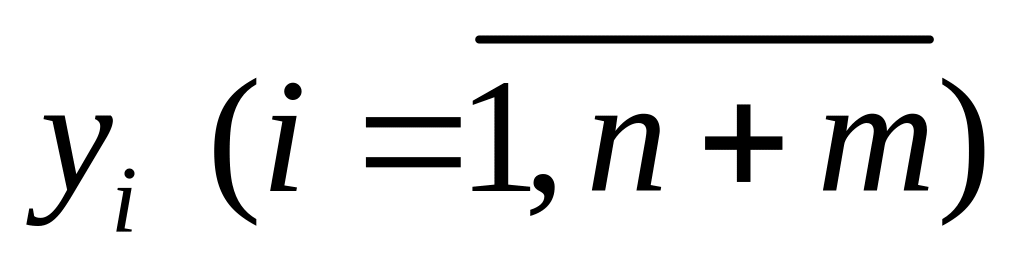 устанавливается взаимно однозначное
соответствие
устанавливается взаимно однозначное
соответствие
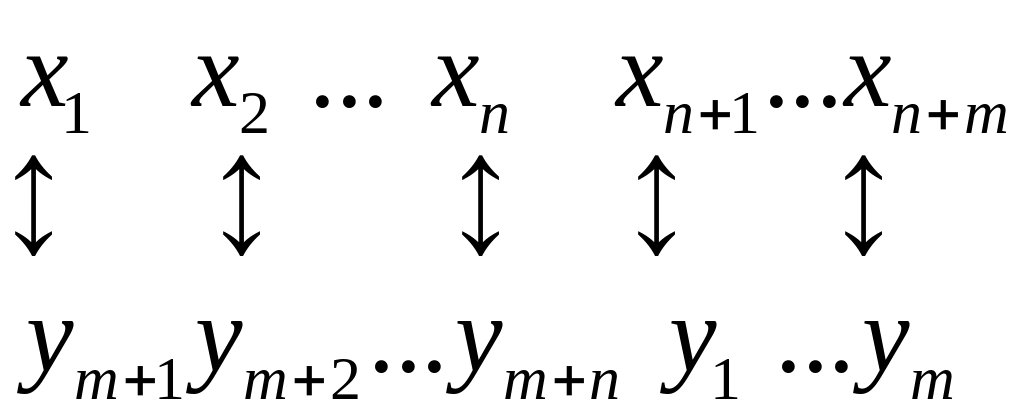 .
.![]()
Замечания.
1. Исходной задачей может быть задача на минимум (1.19) – (1.21), тогда двойственная к ней будет задача на максимум (1.16) – (1.18).
2. В теории двойственности исходная задача должна быть упорядоченной. То есть, если целевая функция задачи максимизируется, то ограничения – неравенства должны быть вида « », если минимизируется, то вида « ». Если в некоторых ограничениях это условие не выполняется, то их выполнение достигается умножением соответствующих ограничений на (-1).
3. Если на j – переменную исходной задачи не наложено условие неотрицательности, то j – ограничение будет равенством. В противном случае j – ограничение будет неравенством.
4. В двойственной задаче условие неотрицательности накладывается на те переменные, которым в исходной задаче соответствовали ограничения со знаком неравенства.
Любой исходной задаче линейного программирования можно поставить в соответствие двойственную задачу, построенную по правилам, представленным в таблице 1.24.
Таблица 1.24
|
|
|
yi ≥ 0 |
|
yi ≤ 0 |
|
yi — не имеет ограничений на знак |
xj ≥ 0 |
|
xj ≤ 0 |
|
xj — не имеет ограничений на знак |
|
