1. Задачи линейного программирования

1. Постановка задачи

Линейным программированием называется раздел математики, изучающий методы определения условных экстремумов линейных функций.

Задача линейного программирования (ЗЛП) состоит в том, что определяется экстремум (минимум или максимум) функции, которая называется целевой (ЦФ) и зависит от n переменных , при линейных ограничениях, накладываемых на эти переменные. Так как все задачи, рассматриваемые в данной работе, носят экономический характер, то все переменные должны быть больше нуля (естественные ограничения). Следовательно, математическая постановка задачи имеет вид:

1) целевая функция

(1.1)

2) ограничения

		(1.2)
		(1.3)
		(1.4)

3) естественные ограничения

(1.5)

Целевая функция показывает тот эффект, который должен быть получен, в результате решения задачи. Например, максимальная прибыль в результате выпуска той или иной продукции при заданных ограничениях на имеющееся сырьё или минимальные затраты на выпуск той же продукции и другое.

В каждом случае целевая функция имеет своё выражение в зависимости от целей исследования.

В матричной форме постановка задачи имеет вид:

(1.1*)

(1.2*-1.4*)

(1.5*)

Векторы , и в матричной форме будут:

, , ,

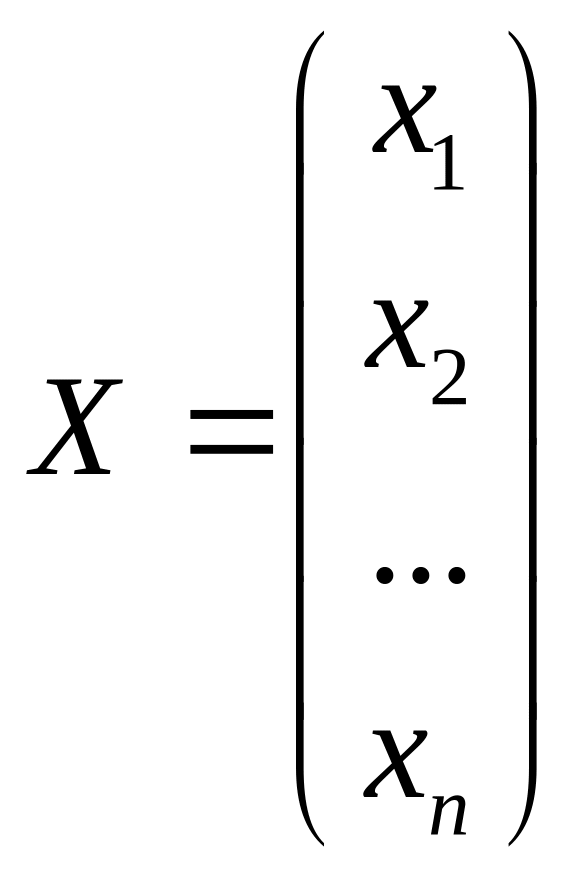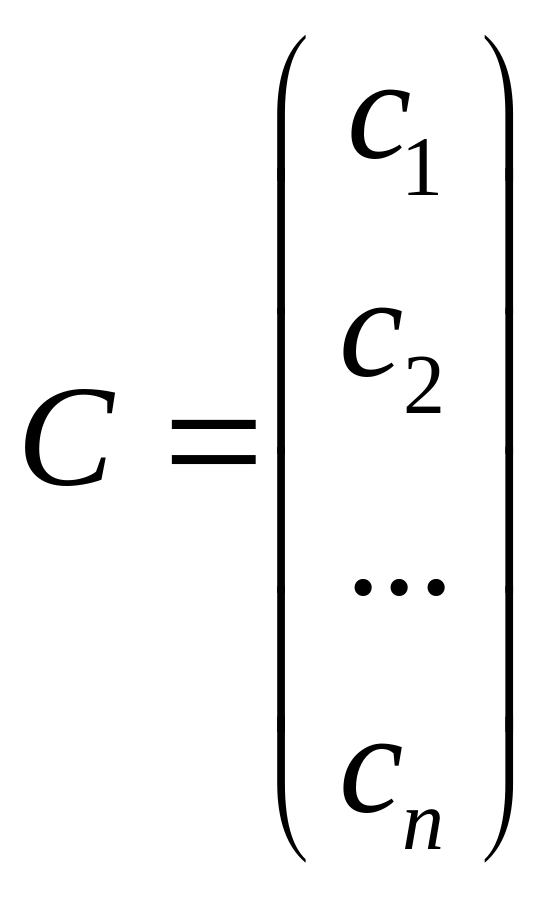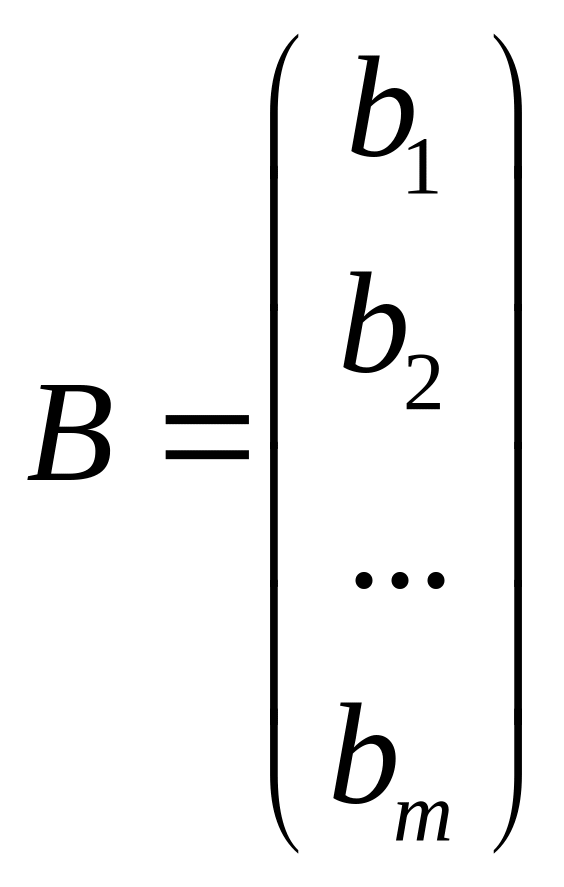и они соответственно называются векторами планов, стоимости и ресурсов (ограничений).

Матрица называется матрицей ограничений (затрат или технологической).

Ограничения (1.2) – (1.4) называются основными, а ограничения (1.5) прямыми или естественными (неосновными).

В дальнейшем для решения задач на максимум будет использоваться обозначение целевой функции F. Для решения задач на минимум – f. В общем случае используется обозначение f, либо в векторной форме, либо - в матричной форме.

Задача с ограничениями ((1.2) или (1.4) называется стандартной или симметричной, если отыскивается максимум (минимум) целевой функции все ограничения, которой записываются со знаками неравенств « » ( « » ).

Если отыскивается максимум (минимум) целевой функции, все ограничения которой имеют вид (1.3), то есть, знак «=», то задача называется канонической или основной.

Вектор , удовлетворяющий системе ограничений задачи, называется планом. Множество планов, удовлетворяющих системе ограничений (1.2), (1.3), называется множеством допустимых планов. Допустимый план , при котором достигается экстремальное значение целевой функции (1.1), называется оптимальным.

Составление математических моделей задач линейного программирования ведётся по следующей схеме.

1. Выбираются переменные . В качестве переменных принимают величины, значения которых однозначно определяют одно из возможных состояний исследуемого процесса.

2. Составляются ограничения (1.2)-(1.4), накладываемые на переменные, выражающие взаимосвязи исследуемого процесса.

3. Составляется целевая функция (1.1).

4. На переменные накладываются естественные ограничения (1.5).

Задачи линейного программирования могут решать проблемы следующих видов.

1) задачи определения оптимального ассортимента продукции (производственные задачи);

2) задачи транспортного типа;

3) задачи составления кормовой смеси (задачи о диете);

4) задачи об оптимальном раскрое;

5) задачи формирования кольцевых маршрутов (задачи коммивояжера);

6) задачи многостороннего коммерческого арбитража.

7) задачи выбора портфеля ценных бумаг и др.

Например, предприятие располагает m видами ресурсов S_i, в количестве b_i и изготавливает n видов продукции. Для изготовления единицы продукции j-го вида ( ) необходимо ресурса i-го вида. Прибыль от реализации единицы продукции j-го вида равна . Определить оптимальный план производства продукции .

Задача линейного программирования имеет вид:

,

- затраты ресурсов не могут превышать имеющихся в наличии

,

- количество выпущенной продукции не может быть отрицательным числом (иногда дополнительно могут накладываться условия целочисленности)

.

Задачу планирования производства можно представить в виде следующей табличной модели.

Таблица 1.1

Ресурс	Расход ресурса на единицу производства продукции				Запас ресурса
	x1	x2	…	xn
S1	a11	a12	…	a1n	b1
S2	a21	a22	…	a2n	b2
…	…	…	…	…	…
Sm	am1	am2	…	amn	bm
Прибыль, у.е.	c1	c2	…	cn	ЦФ

Пример 1. Определение оптимального ассортимента продукции (производственная задача).

Пусть определённая фирма выпускает два вида продукции П1 и П2, на производство которых используется сырьё трёх типов А, В и С. Затраты сырья на единицу продукции и доход (в условных единицах), получаемый фирмой от реализации единицы продукции, приведены в таблице 1.2

Таблица 1.2

Сырьё	Продукция		Количество сырья
	П1	П2
А	4	2	100
В	2	3	400
С	3	1	300
Доход на единицу продукции	8	9

Требуется так организовать работу фирмы, чтобы её доход был максимальным.

Решение.

1. Примем: - количество продукции П1, выпускаемой фирмой; – количество продукции П2.

2. Целевая функция должна отражать максимальный доход, получаемый фирмой:

.

3. Составляем систему ограничений. На производство продукции фирма может израсходовать сырья не больше, чем у неё имеется. С учётом количества сырья определённого типа на производство каждого вида продукции, составляем неравенства

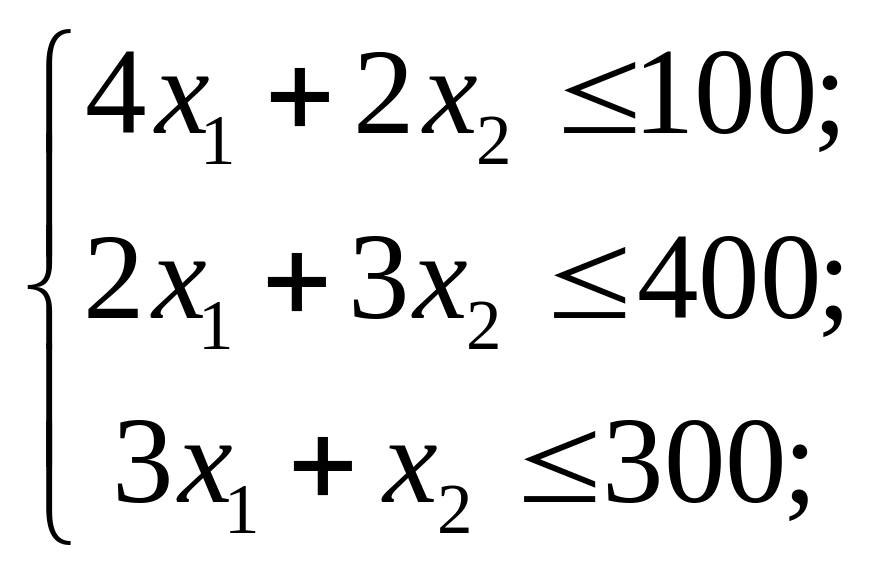
То есть, математическая модель задачи в соответствие с (1.1)-(1.5) имеет вид:

,

Пример 2. Птицефабрика выращивает кур, гусей и уток., на кормление которых используется корм двух видов А и В. Количество выращиваемой птицы должно быть не менее заданной нормы. Необходимое количество корма на одну птицу, и его стоимость приведены в таблице 1.3 (в условных единицах). Требуется так организовать работу птицефабрики, чтобы её расходы были минимальными.

Таблица 1.3

Виды птиц	Стоимость видов корма (в усл.ед) на одну птицу		Нормы производства птицы
	А	В
Куры	0,6	0,3	300
Гуси	0,2	0,4	150
Утки	0,15	0,15	200
Стоимость корма (в усл.ед)	12	40

Решение. Переменными являются количества разводимых птиц:

1. - количество расходуемого корма А, - корма В.

2. Целевая функция будет отражать минимальные расходы фабрики

.

3. Система ограничений будет отражать затраты на корм птиц

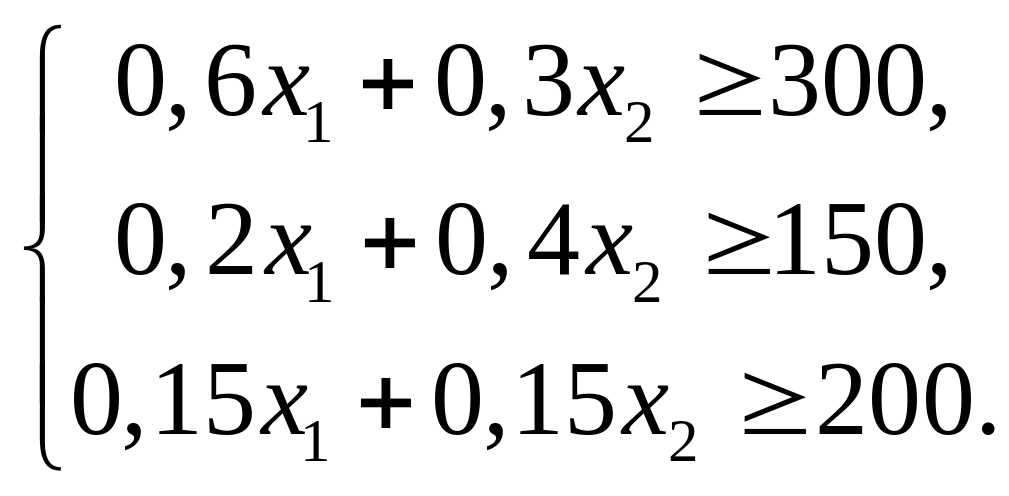
Учитывая положительность естественных ограничений

,

математическая модель задачи будет иметь вид:

.
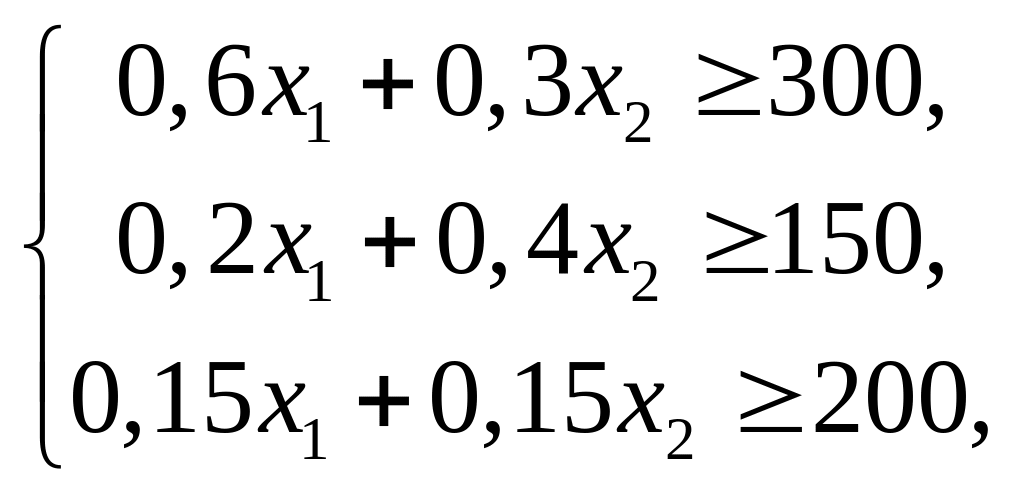