Задачи для решения

5. Найти решение следующих задач через двойственные к ним.

5.1. 5.2.

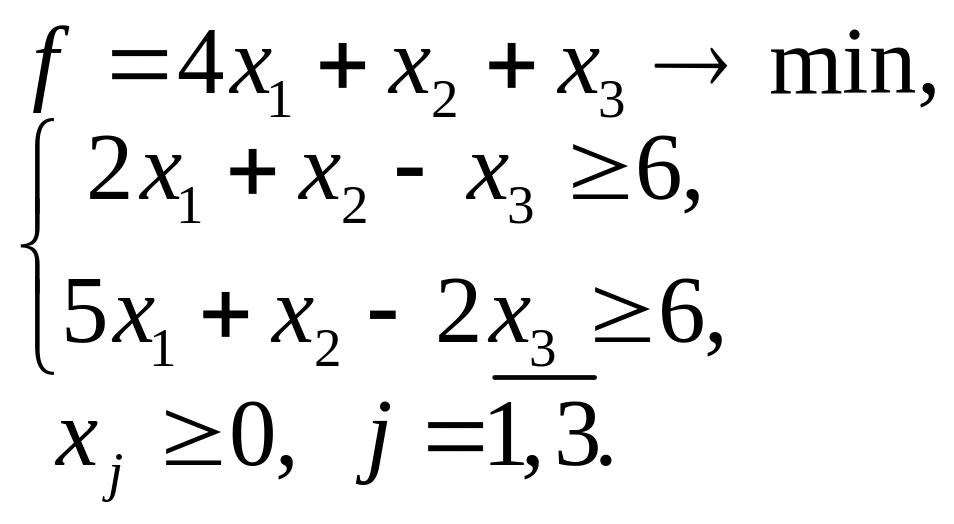
5.3. 5.4.

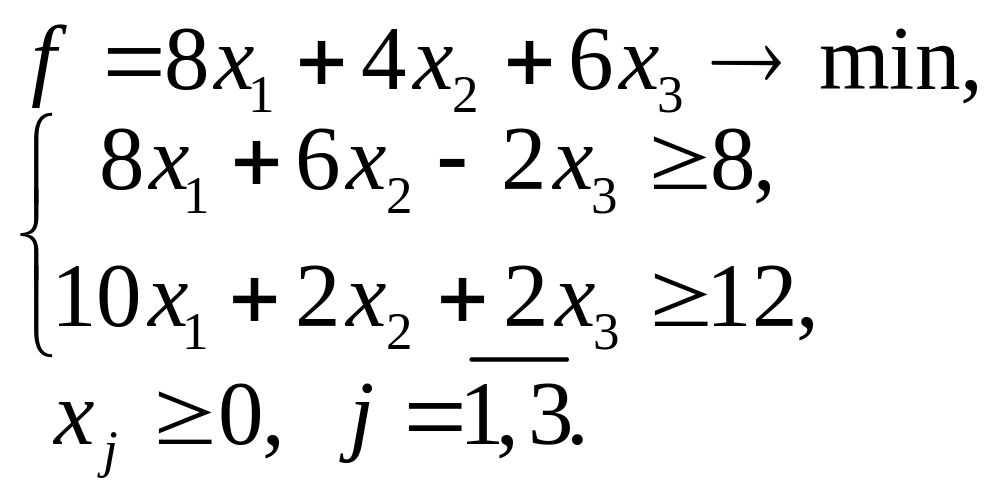
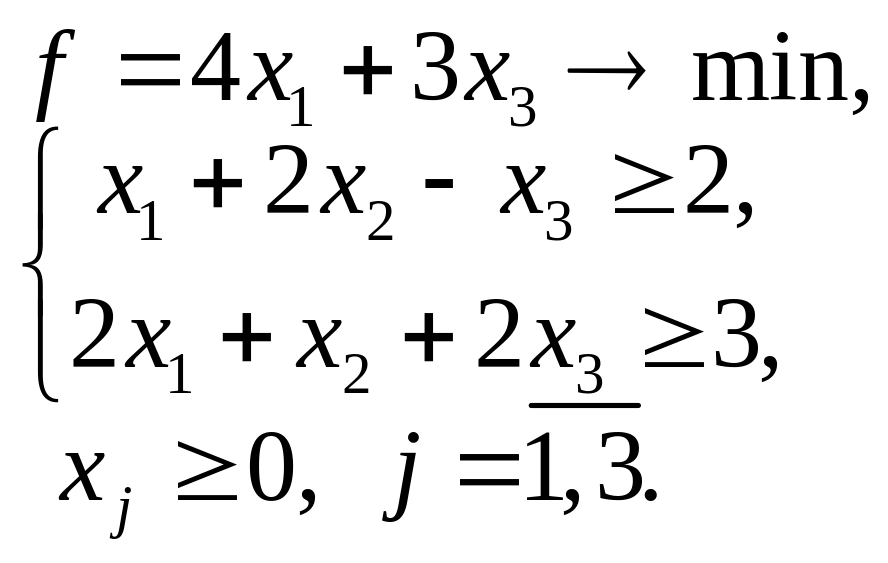
5.5. 5.6.

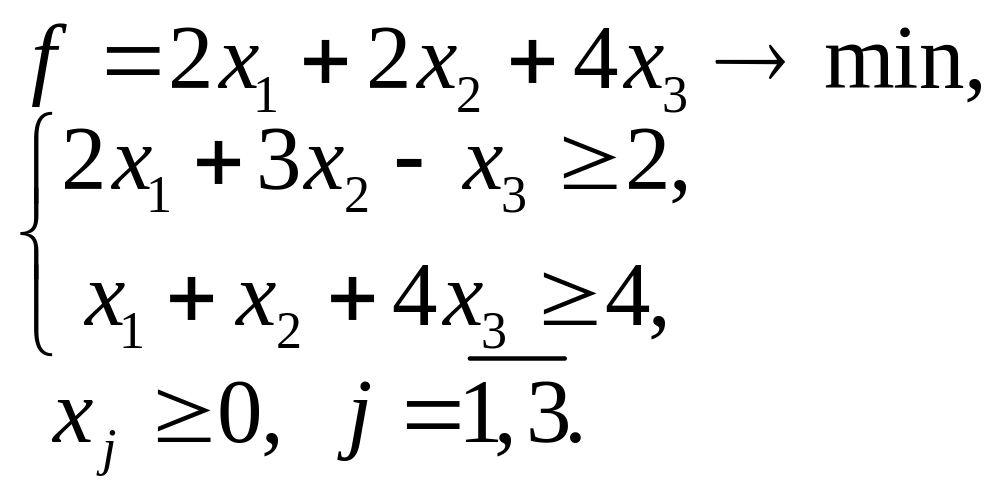
5.7. 5.8.

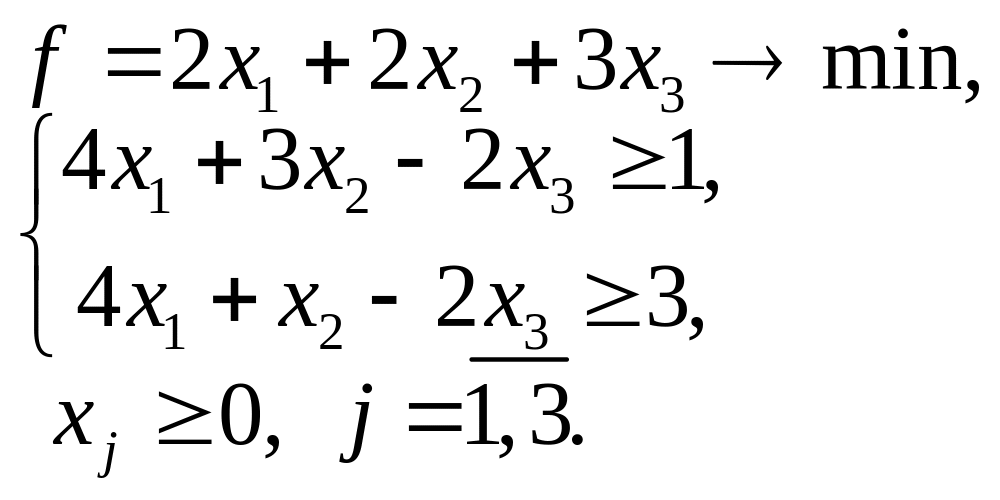
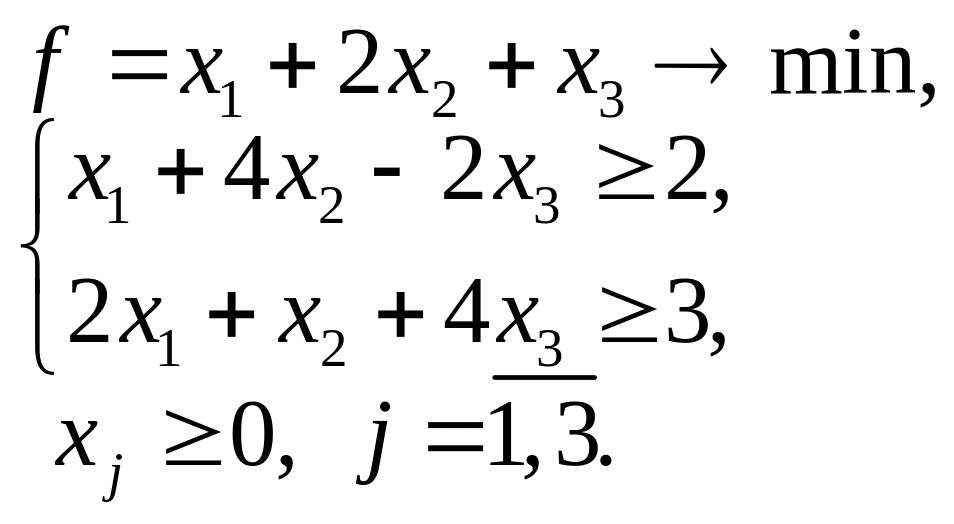
5.9. 5.10.

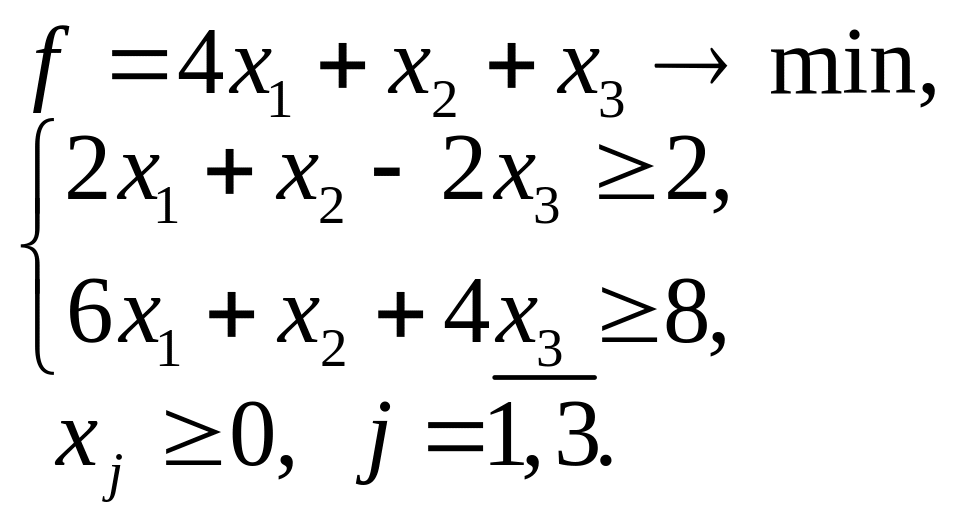
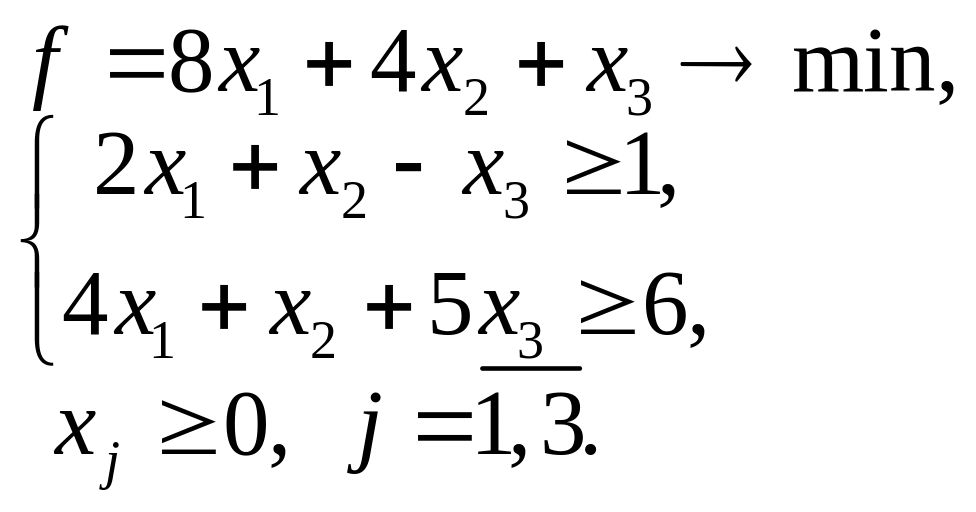
5.11. 5.12.

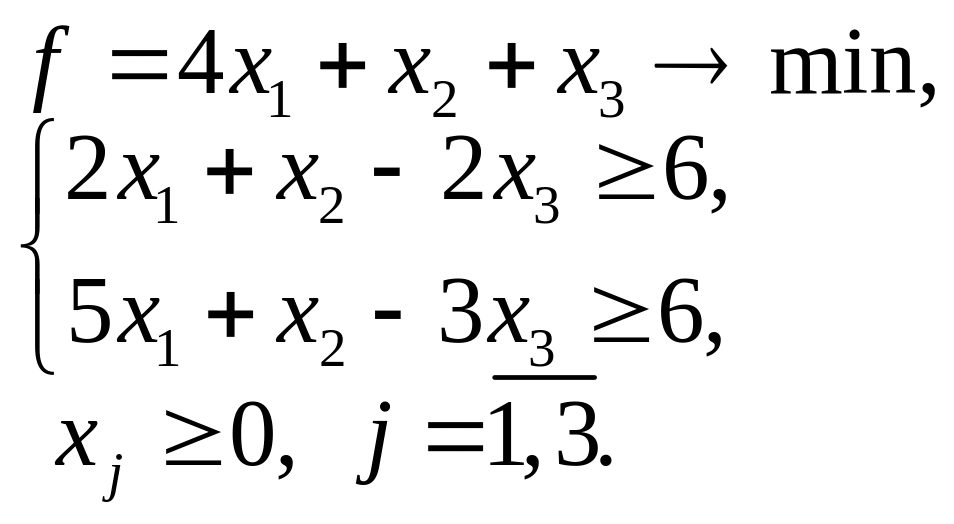
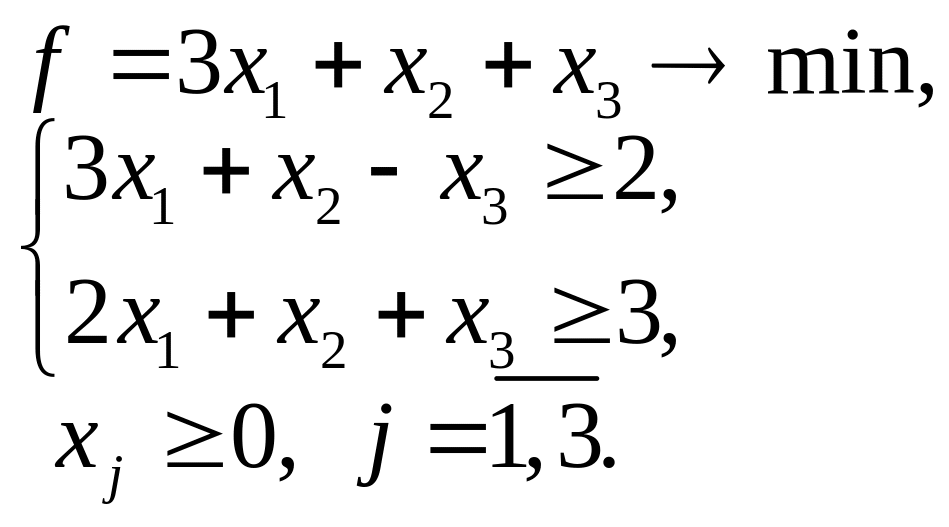
5.13. 5.14.

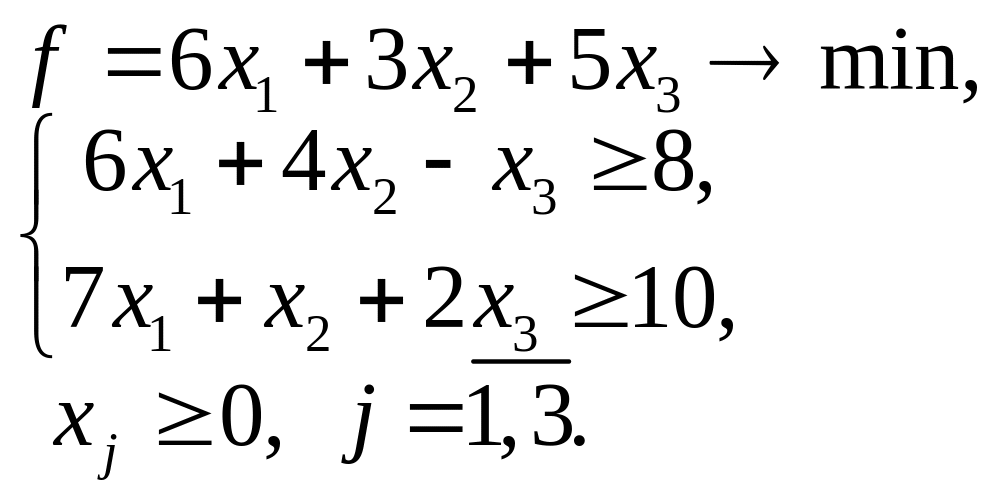
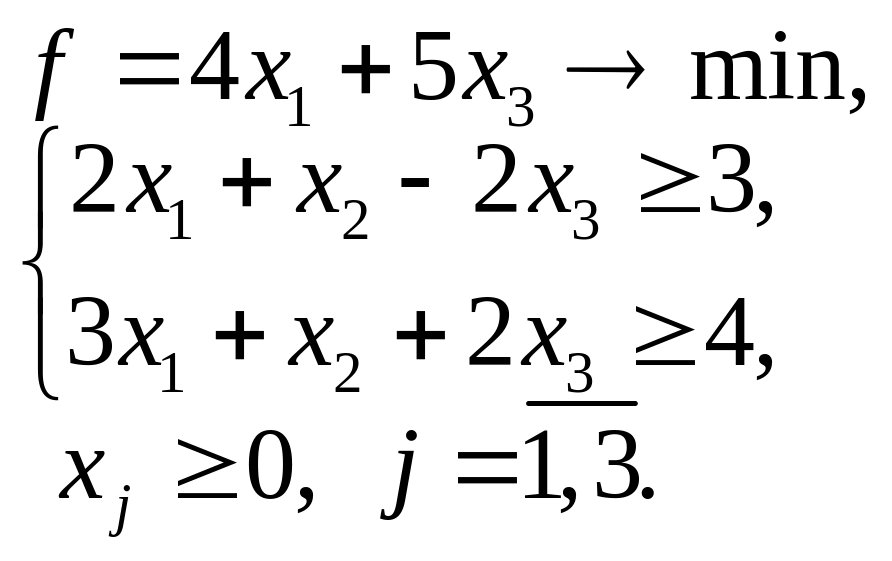
5.15. 5.16.

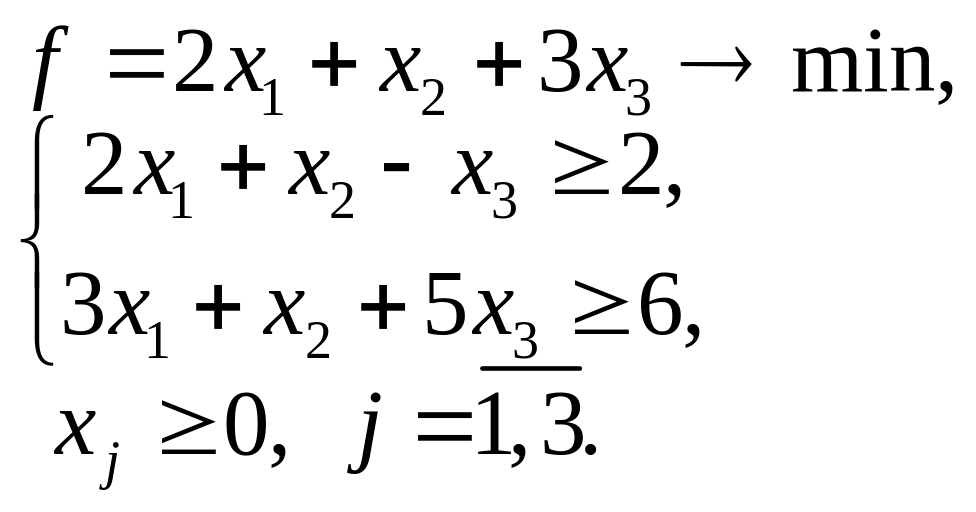
5.17. 5.18.

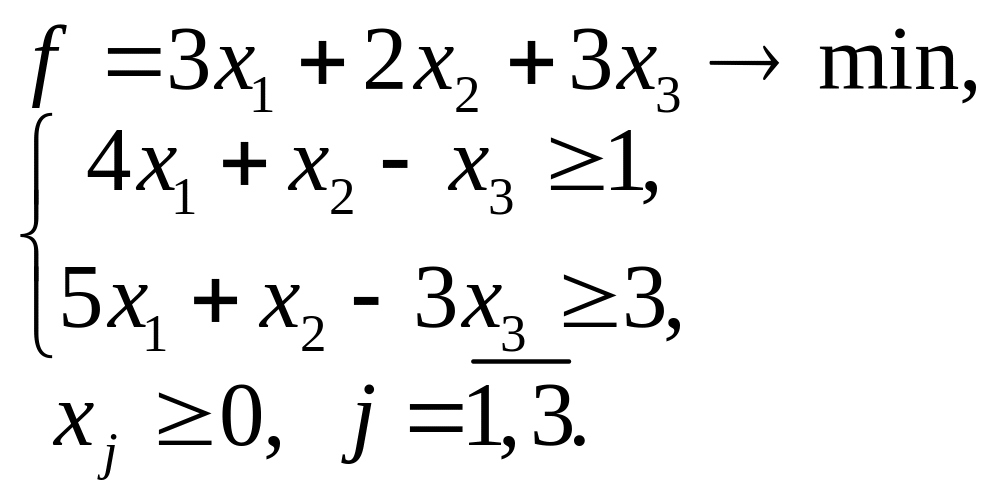
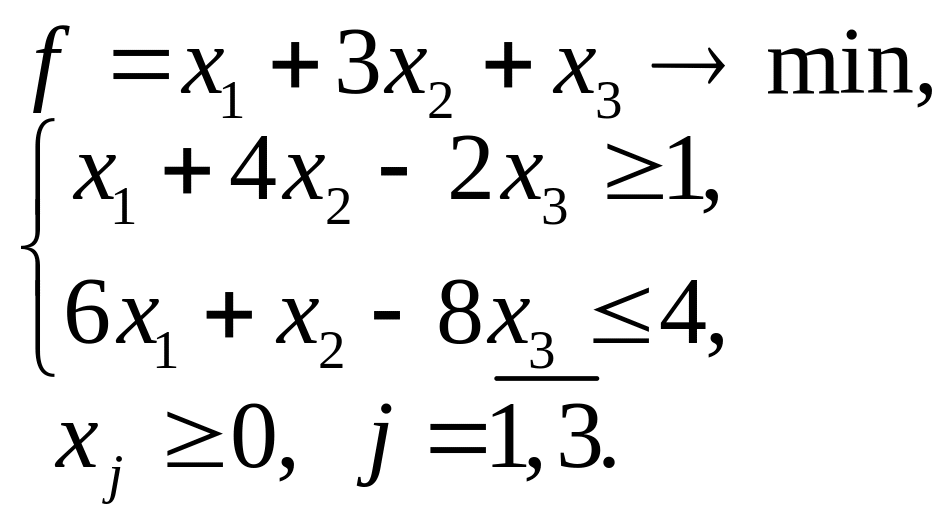
1.5.3. Геометрическая интерпретация двойственных задач

Если число переменных прямой и двойственной задач, образующих пару двойственных задач, равно двум, то при использовании геометрической интерпретации задачи линейного программирования, можно найти решение данной пары двойственных задач. Тогда, имеет место один из следующих случаев:

1) обе задачи имеют оптимальные планы;

2) планы имеет только одна задача;

3) для каждой задачи двойственной пары множество планов пусто.

Пример 15. Пусть дана пара двойственных задач. Найти графическое решение обеих задач.

Прямая задача Двойственная задача

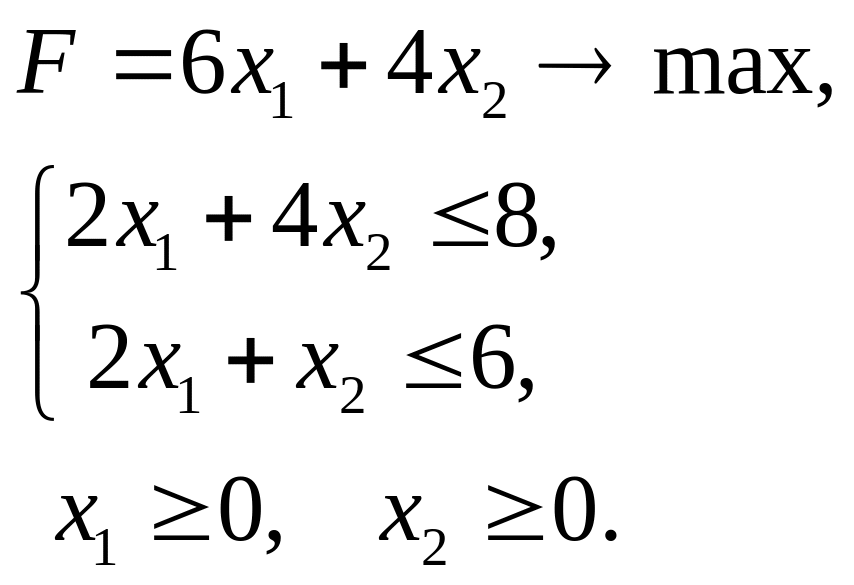
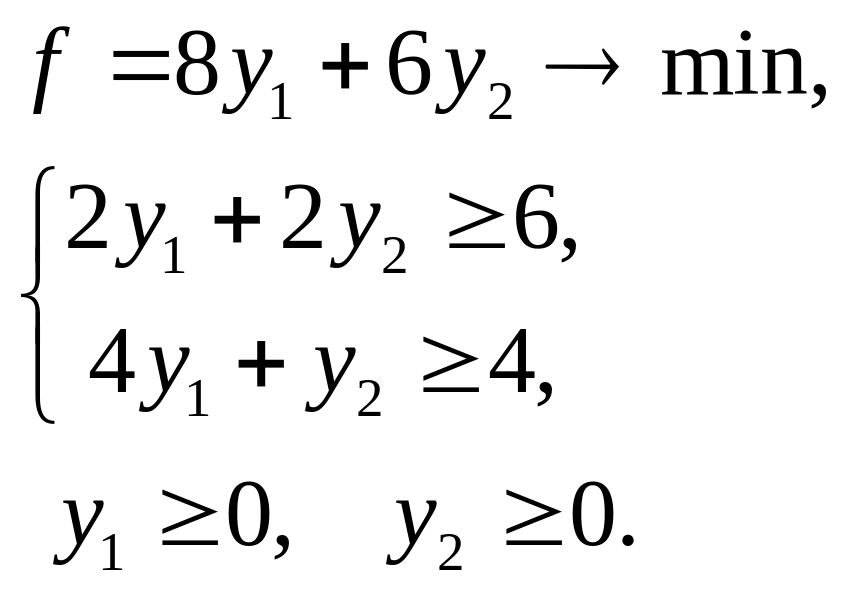
Решение. Обе задачи содержат по две переменных. Следовательно, они разрешимы. По системе ограничений исходной задачи строим область допустимых решений (Рис.1.13). Затем строим линию уровня для функции , и передвигаем её параллельно самой себе в направлении вектора , пока не достигнем крайней точки области допустимых решений.

Этой точкой будет являться точка А(8/3;2/3), то есть, . В точке А целевая функция достигает максимума .

Графическое решение для двойственной задачи (Рис 1.14). Строим область допустимых решений в соответствие с ограничениями. Затем строим линию уровня для функции , и перемещаем её параллельно самой себе в направлении вектора до тех пор, пока она коснётся области допустимых решений. Этой точкой будет являться точка В(1/3;8/3), то есть . В точке В целевая функция достигает минимума и будет равна .

Между переменными существует взаимно однозначное соответствие .

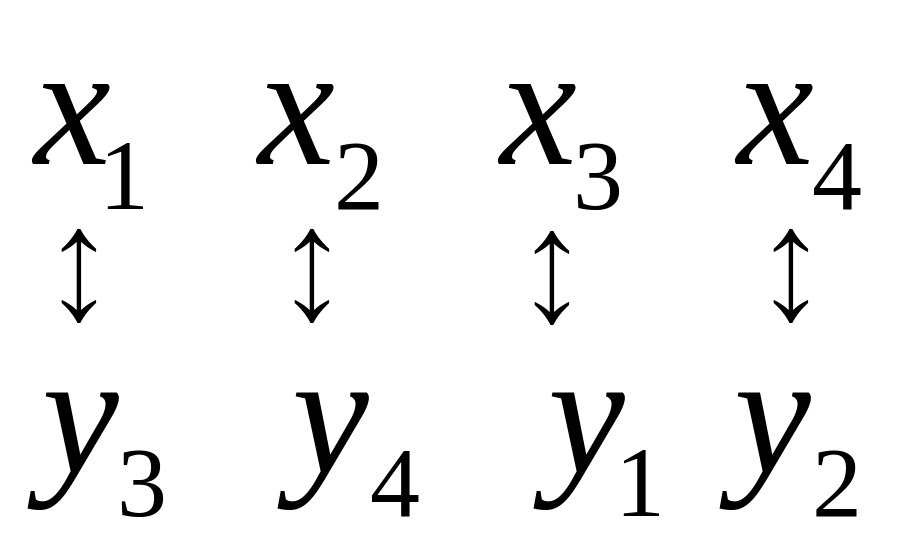Базисным переменным исходной задачи и соответствуют свободные переменные двойственной и . Свободным переменным исходной задачи и , соответствуют базисные переменные двойственной и .

1.5.4. Двойственный симплекс – метод

Для решения задач линейного программирования кроме прямого симплексного метода, изложенного в п.3.2, используется двойственный симплекс метод. В этом случае решение задачи распадается на два этапа. На первом этапе определяется начальный опорный план, его называют псевдопланом, для этого исключаются отрицательные коэффициенты в f – строке (для задачи на минимум, когда все коэффициенты этой строки записываются со своими знаками). На втором этапе определяется оптимальный план, для чего избавляются от отрицательных элементов в столбце свободных членов.

Алгоритм двойственного симплекс – метода состоит в следующем.

Этап 1. Определение начального опорного плана (псевдоплана).

Заполняем исходную симплексную таблицу.

1.1. Просматриваем коэффициенты f - строки симплексной таблицы. Если среди них нет отрицательных, то делаем переход к пункту 2.1 поиска оптимального плана.

1.2. Если в f - строке имеются отрицательные элементы, то делаем следующие преобразования.

- Выбираем в f - строке наибольший по абсолютной величине.

- В выделенном столбце находим наименьший отрицательный элемент, и содержащая его строка будет разрешающей. Если в выделенном столбце нет отрицательных чисел, то задача не имеет решения.

- Определяем отношения элементов f - строки к соответствующим элементам разрешающей строки и по наименьшему из этих отношений определяем разрешающий столбец.

- Пересечение разрешающего столбца и разрешающей строки определяет разрешающий элемент.

1.3. По найденному разрешающему элементу делаем шаг симплексных преобразований.