1.4.2.Симплексный метод

Аналитическое решение задачи линейного программирования осуществляется в следующей последовательности.

1. Задача приводится к каноническому виду.

2. Выбираются базисные и свободные переменные. Переменные являются базисными, если они линейно независимы и соответствуют единичным векторам (чаще всего это балансовые переменные):

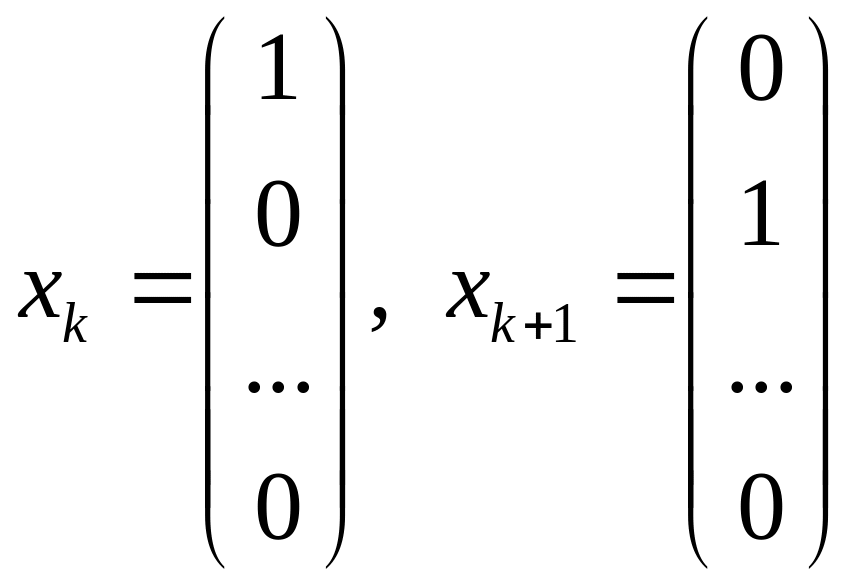и так далее.

Если в исходных ограничениях нет базиса, то он вводится в них искусственно.

3. Целевая функция выражается через свободные переменные.

4. Находится решение, приводящее целевую функцию к экстремуму.

Обычно задача поиска оптимального плана состоит из задачи определения какого-либо опорного плана , затем его оптимизации, то есть, последовательного перебора опорных планов таким образом, чтобы целевая функция возрастала (или не убывала). Геометрически это означает переход по рёбрам многогранника (по граничным прямым в случае многоугольника), являющегося областью решений, из одной вершины в другую и далее до достижения оптимального решения .

Пусть задача (1.1)-(1.5) максимизируется и система ограничений записана в симметричной форме

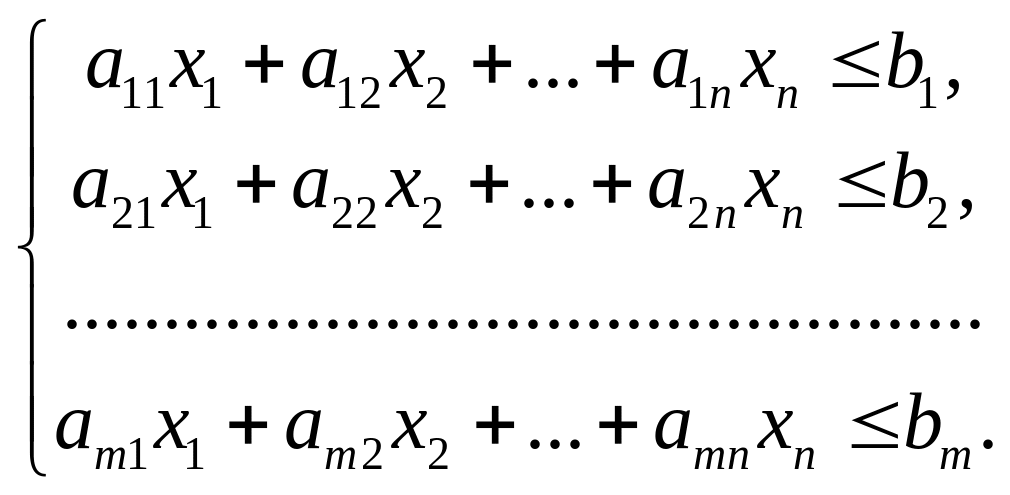(1.7)

За счёт введения балансовых переменных задача приведена к каноническому виду (1.8) с условиями (1.9)

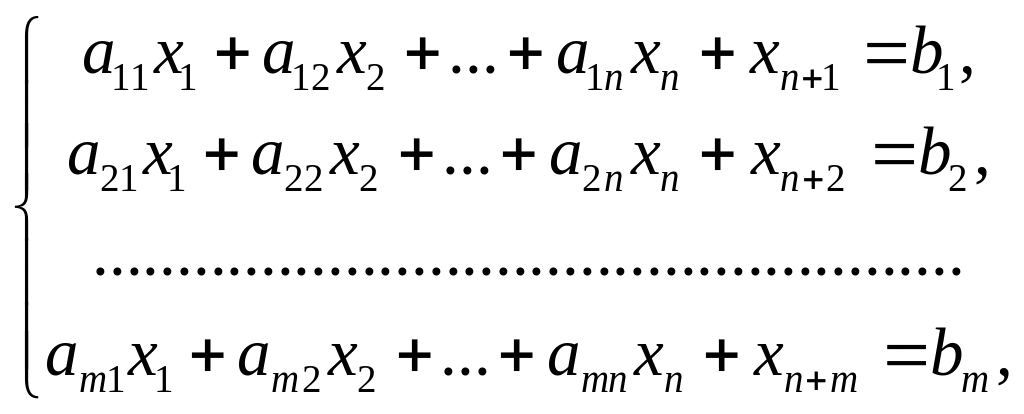(1.8) (1.9)

Если балансовые переменные принять за базисные и выразить их через остальные переменные

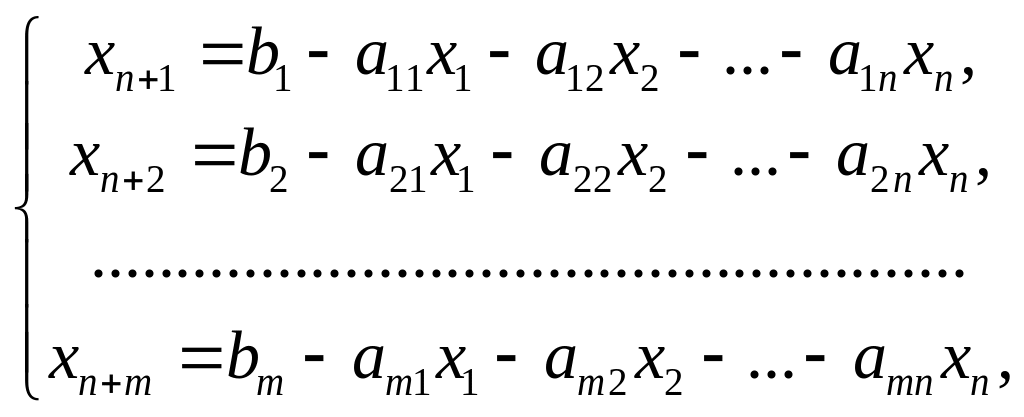
то дальнейшие вычисления удобно свести в таблицу вида 1.5, которая называется симплексной

Таблица 1.5

Б.П.	1	С.П.
				…
= = … =	…	…	…	… … … … …	…
=				…

В первом столбце таблицы 1.5 приводятся базисные переменные (Б.П.). Во втором столбце – свободные члены. В столбцах (С.П.) приводятся свободные переменные с отрицательными знаками при переменных, за счёт чего коэффициенты при этих переменных остаются с такими знаками, как в системе неравенств. Последняя строка таблицы называется - строкой. Коэффициенты целевой функции также записываются с противоположными знаками и называются оценками.

Алгоритм поиска решения будет следующим.

Этап 1. Определение начального опорного плана.

Просматриваем столбец свободных членов таблицы 1.5, если в нём все элементы положительны, то приравниваем свободные переменные к нулю и имеем опорный план . Тогда можно перейти к поиску следующего опорного плана для оптимизации решения. Если найдётся хотя бы один отрицательный свободный член, то план не является опорным. Чтобы сделать план опорным, составляем следующую таблицу.

1. Выполняем следующие действия.

- Просматриваем строку, соответствующую отрицательному свободному члену, и выбираем в ней наименьший отрицательный элемент. Если отрицательных элементов в строке нет, то решения не существует. Столбец, содержащий выбранный отрицательный элемент, принимаем за разрешающий. Если одинаковых отрицательных элементов несколько, то выбираем любой из них.

- Находим отношение элементов столбца свободных членов к соответствующим элементам разрешающего столбца (симплексные отношения). Можно справа добавить к таблице ещё один столбец и поместить в нём симплексные отношения. Это будет симплексный столбец (С.С.). Выбираем из полученных частных наименьшее. Берётся только отношение элементов с одинаковыми знаками. Наименьшее частное будет определять разрешающую строку. - Пересечение разрешающего столбца и разрешающей строки определяют, соответственно, разрешающий элемент.

1.2. Делаем шаг симплексных преобразований. Составляем новую таблицу, в которой:

- Разрешающий элемент заменяется обратной величиной.

- Остальные элементы разрешающей строки и разрешающего столбца делятся на разрешающий элемент. Для решения задачи максимизации функции при делении элементов столбца знаки меняются на противоположные (для минимизации – знаки строки меняются на противоположные).

- Базисная переменная строки и свободная переменная столбца меняются местами.

Замечание. 1*. Если в разрешающем столбце есть нулевой элемент, то строка, в которой он находится, остаётся без изменений.

Если в разрешающей строке есть нулевой элемент, то соответствующий столбец, остаётся без изменений.

2*. Если в процессе вычислений образуется строка, полностью состоящая из нулей, то она может быть отброшена.

1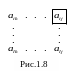 .3. Все остальные элементы таблицы преобразуются по правилу прямоугольника. Пусть элемент является разрешающим, тогда элемент очередного опорного плана расположенный как на рис.1.8, вычисляется по формуле

. (1.10)

Т о есть, из произведения элементов, стоящих на главной диагонали (главной считается та диагональ, на которой стоит разрешающий элемент) вычитается произведение элементов, стоящих на побочной диагонали , и эта разность делится на разрешающий элемент .

Иногда вместо правила прямоугольника используют правило треугольника. Если в выражении для элемента новой таблицы разделить оба слагаемых правой части на разрешающий элемент , то получится выражение

. (1.10*)

Оно представляет собой разность между исходным значением элемента с индексами и выражением, вычисленным по правилу треугольника, то есть произведение элементов, стоящих в вершинах и , делённых на разрешающий элемент , стоящий в третьей вершине .

Этап 2. Определение оптимального опорного плана.

Пусть существует начальный опорный план решения задачи на максимум и необходимо найти оптимальный план.

1. Просматриваем F – строку.

- Выбираем в качестве разрешающего столбца тот, где отрицательный элемент является наибольшим по абсолютной величине. Если таких элементов несколько, то берём любой из них.

- Находим отношения элементов столбца свободных членов к элементам разрешающего столбца. Это симплексные отношения, они вычисляются только для положительных элементов столбца. По наименьшему из них находим разрешающую строку.

- На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.

2.2 Делаем обычный шаг симплексных преобразований. Составляем новую таблицу, в которой:

- разрешающий элемент заменяется обратной величиной;

- элементы разрешающей строки делятся на разрешающий элемент;

- элементы разрешающего столбца делятся на разрешающий элемент, и знаки меняются на противоположные;

- все остальные элементы новой таблицы находятся по правилу

прямоугольника;

- базисная переменная, стоящая в базисном столбце и свободная переменная, стоящая в строке свободных переменных меняются местами;

- если в процессе решения в столбце свободных членов вновь появляется отрицательный элемент, то возвращаемся к пункту 1.1 и повторяем все вычисления.

Замечание. Если в разрешающем столбце есть нулевой элемент, то строка, в которой он находится, остаётся без изменений.

Если в разрешающей строке есть нулевой элемент, то соответствующий столбец, в котором он находится, остаётся без изменений.

При оптимизации решения все вычисления пунктов 2.1.-2.2. повторяются до тех пор, пока все коэффициенты F –строки не станут положительными. Тогда значение целевой функции достигло максимального значения, а найденный вектор является оптимальным при нулевых свободных переменных и положительных базисных переменных, расположенных в первом столбце таблицы.

Замечание. Если все элементы F –строки отличны от нуля, то существует единственное решение для оптимального плана. Если среди элементов есть хотя бы один, равный нулю, то оптимальных планов будет бесконечной множество. В таком случае любая выпуклая линейная комбинация оптимальных опорных планов

,

где , будет оптимальной.

Существование неединственного оптимального решения удобно с практической точки зрения. Варьируя параметры , можно выбрать оптимальный план, который по другим показателям, не учтённым целевой функцией, будет наилучшим. Геометрически бесконечное множество решений означает, что все оптимальные планы попали на одно и то же ребро многогранника решений. В двумерном случае - решение попало на одну из сторон многоугольной области допустимых планов.

При решении задачи на минимум:

- знаки элементов в f – строке первоначально – положительны, после всех преобразований они должны измениться с положительных на отрицательные;

- знаки меняются при делении элементов разрешающей строки на разрешающий элемент;

- знаки не меняются при делении элементов разрешающего столбца на разрешающий элемент.

Все остальные операции производятся по тем же правилам, что и при решении задачи на максимум.