Этап 2. Определение оптимального плана.

2.1. Просматриваем столбец свободных членов. Если среди них нет отрицательных элементов, то оптимальное решение достигнуто.

2.2. Если в столбце свободных членов есть отрицательные элементы, то делаем следующие преобразования.

- отрицательных элементов выбираем наименьший. Этот элемент определяет разрешающую строку.

- Определяем отношения элементов f - строки к соответствующим отрицательным элементам разрешающей строки. Выбираем наименьшее по абсолютной величине отношение. Оно будет определять разрешающий столбец и, следовательно, разрешающий элемент. Если в разрешающей строке нет положительных элементов, то задача не имеет решения.

2.3. С найденным разрешающим элементом делается шаг симплексных преобразований.

Замечание. При решении задачи на максимум необходимо сделать замену f = - F и находить минимум полученной функции f, взятому со знаком минус.

Пусть исходная двойственная задача сформулирована в виде

при ограничениях

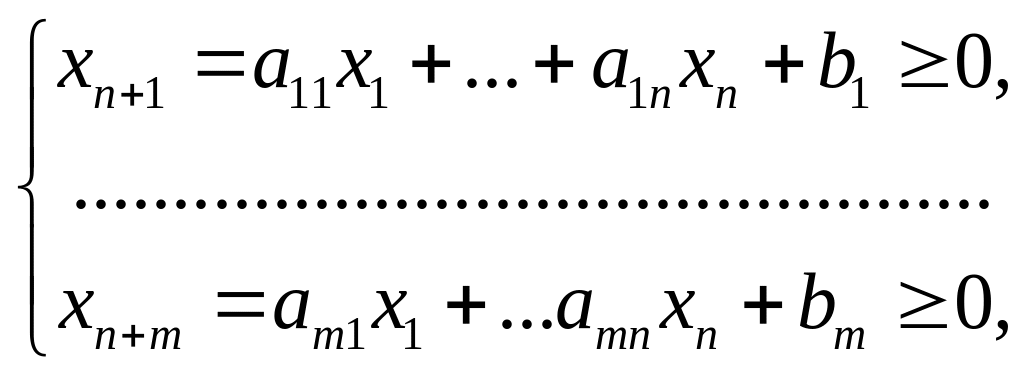
Вычисления удобно проводить, используя следующую таблицу

Таблица 1.29

Б.П.	1	С.П.
			…
=			…
…	…	…	…	…
=			…
f =			…

Пример 16. Двойственным симплекс-методом найти решение задачи

.

Решение. Так как в f - строке имеется отрицательная оценка

(-4), то второй столбец таблицы 1 считается выделенным, то есть, разрешающим. В нём содержится единственное отрицательное число (-2). Строка, содержащая этот элемент, будет разрешающей и, соответственно, разрешающим является элемент (-2).

Таблица 1.30 Таблица 1.31

Б.П.	1	С.П.			Б.П.	1	С.П.
=	8	2			=	4	1	-1/2
=	10	-1	4		=	26	3	-2
=	-12	2	2		=	-4		-1
f =	0	4	-4		f =	-16	0	2

Находим отношения

.

Из двух одинаковых отношений можем выбрать любое. Например, возьмём второй столбец. Делаем шаг симплексных преобразований (табл.2).

Смотрим элементы f - строки таблицы 1.30. Среди них нет отрицательных. Поэтому переходим ко второму этапу алгоритма - находим оптимальный план.

Просматриваем элементы столбца свободных членов. Среди них есть отрицательный элемент (-4). Следовательно, полученный план не является оптимальным. Принимаем строку, содержащую этот элемент, за разрешающую. Так как в f - строке есть нуль, то имеет место случай вырождения. Над нулём имеется элемент, равный 4, следовательно, этот элемент будет разрешающим. Соответственно, разрешающим будет первый столбец. С этим разрешающим элементом делаем шаг симплексных преобразований (табл.1.32).

Таблица 1.32

Б.П.	1	С.П.
=	5
=	29
=	1
f =	-16	0	2

Найденный план является оптимальным

(1;5;0;29;0).

Минимальное значение функции f

.

Пример 17. Найти решение двойственным симплекс – методом задачу

.

Решение. Двойственной к исходной задаче будет:

.

Приведём ограничения к каноническому виду:

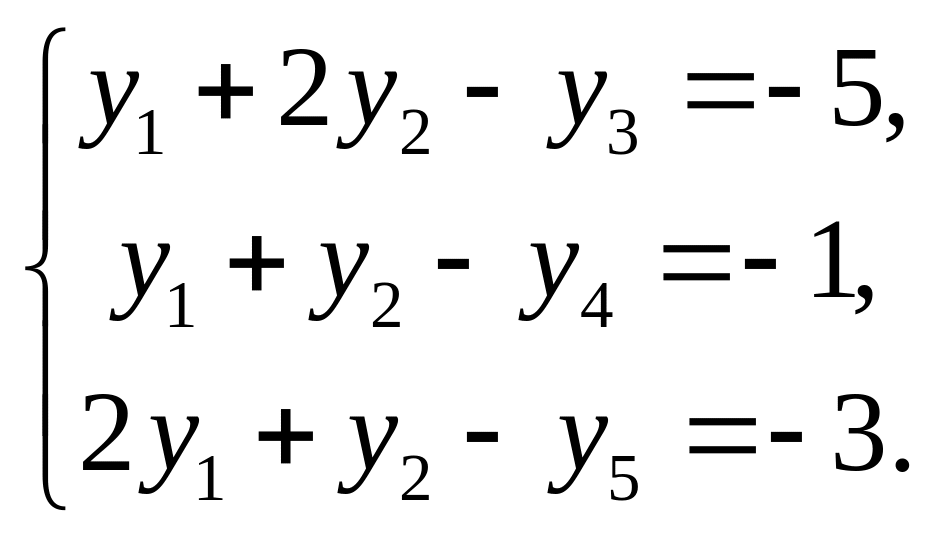
Выразим базисные переменные

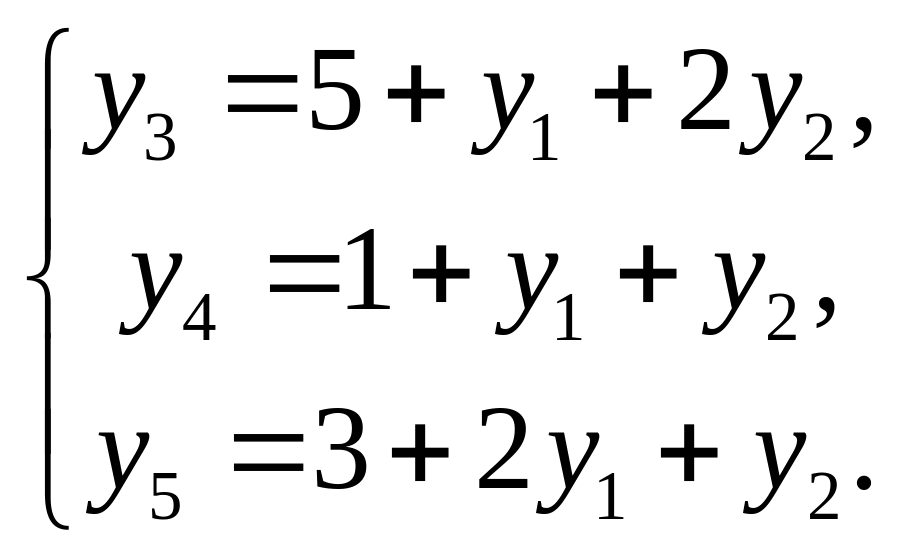
Исходная таблица будет иметь вид (табл.1.33)

Таблица 1.33 Таблица 1.34

Б.П.	1	С.П.			Б.П.	1	С.П.
		-	-				-	-
=	5	-1			=	5/2	-1/2	-1/2
=	1	-1	-1		=	-3/2	-1/2
=	3	-2	-1		=	1/2	-3/2	1/2
f =	0	-1	-2		f =	-5	0	1

В f- строке выделяем отрицательную оценку (-2). Столбец под будет выделенным. В нём есть отрицательные элементы. Следовательно, задача имеет решение. Фиксируем этот элемент. Строка с будет разрешающей. Находим .

Из двух одинаковых отношений выберем, например, первое. Тогда столбец под будет разрешающим. С разрешающим элементом (-2) делаем шаг симплексных преобразований, получаем таблицу 1.34.

В полученной таблице нет оптимального решения, так как в столбце свободных членов есть отрицательный элемент (-3/2). Делаем следующие преобразования. Строка с будет разрешающей, а элемент (1/2) разрешающим элементом. С этим элементом делаем шаг симплексных преобразований (табл.3).

Таблица 1.35

Б.П.	1	С.П.
		-	-
=	1
=	3
=	2
f =	-2	1	2

Среди элементов столбца свободных членов нет отрицательных. Следовательно, полученное решение является оптимальным

(0;1;3;0;0).

Минимальное значение функции

-2.

Задача, двойственная к задаче об ассортименте продукции, имеет вид:

,

y₁ ³ 0, y₂ ³ 0, y₃ ³ 0, y₄ ³ 0.