Решение типовых задач к вопросу: Статистические методы прогнозирования рядов динамики.

Задача №1

Проверка гипотезы на существование тренда.

В таблице 1. представлены годовые данные об урожайности зерновых культур.

Таблица 1 Урожайность зерновых культур п/га

t	1	2	3	4	5	6	7	8	9		10	11
yt	6.7	7,3	7.6	7,9	7,4	8,6	7,8	7,7	7,9		8,2	А
12	13	14	15	16	17	18		19		20		21
9,1	8,3	8,7	8,9	9,1	9,5	10,4		10,5		10,2		9.3

Определить: существует ли тенденция в исследуемом процессе.

Решение:

Процесс формирования серий показан в таблице 2. Во второй строке этой таблицы в соответствии указан «+», если последующее значение уровня ряда больше предыдущего,

« -» , если - меньше.

Таблица 2 Формирование серий

i	1	2	3	4	5	6 ,	7	8	9	10
	+	+	+	-	+	-	-	+	+	+
11	12	13	14	15	16	17	18	19	20
+	-	+	+	+	+	+	+	-	-

Анализ полученной последовательности знаков позволил число серий v(21 )=8 протяженность самой длинной серии (21) = 6

Табличное значение (см.табл.1.8.2.) (21) = 6

Делаем проверку. Для этого сначала определим значение для правой части первого неравенства:

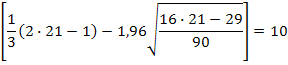
Тогда проверка выполнения условий показывает, что оба неравенства не выполняются. Следовательно, нулевая гипотеза отвергается, динамика временного ряда характеризуется наличием систематической составляющей - в изменении урожайности присутствует динамика.

Задача № 2.

Методы сглаживания временных рядов.

По данным об урожайности (табл. 1) за 16 лет рассчитайте: трех-, семилетние скользящие средние и графически сравните результаты; пятилетнюю взвешенную скользящую среднюю.

Таблица1. Урожайность пшеницы, ц/га

t	1	2	3	4	5	6	7	8
yt	10,3	14,3	7,7	15,8	14,4	16,7	15,3	20,2
t	9	10	11	12	13	14	15	16
yt	17,1	7,7	15,3	16,3	19,9	14,4	18,7	20,7

Решение:

1. Результаты расчетов представлены в табл.2.

Таблица 2. Расчет скользящих средних

t	yt	i=3	i=7		i=5
1	2	3		4	5
1	10,3	-		-	-
2	14,3	10,8		-		-
3	7,7	12,6		-		11,9
4	15,8	12,6		13,5		12,6
5	14,4	15,6		14,9		16,2
6	16,7	15,5		15,3		15,2
7	15,3	17,4		15,3		17,4
8	20,2	17,5		15,2		18,8
9	17,1	15,0		15,5		15,2
10	7,7	13,4		16,0		11,7
1	2	3		4		5
11	15,3	13,1		15,8		12,5
12	16,3	17,2		15,6		18,1
13	19,9	16,9		16,1		17,3
14	14,4	17,7		-		17,3
15	18,7	17,9		-		-
16	20,7	-		-		-

При трехлетней скользящей средней (i=3)

и т.д.

При семилетней скользящей средней (i=7)

и т.д.

2. Для вычисления значений пятилетней взвешенной скользящей средней воспользуемся таблицей 1. Тогда

И т.д.

Задача № 3,

Пусть сглаживание осуществляется по пятичленной скользящей средней (I=5), причем аппроксимация осуществляется квадратичным полиномом (m=2). Требуется определить весовые коэффициенты для восстановления двух последних уровней рада.

Решение:

Осуществим перенос начала координат в середину активного участка:

t=-2;-1;0;+1;+2;

После этого система нормальных уравнений примет вид:

(1.8.53)

Из первого и третьего уравнений определим выражение для коэффициента a₀:

или в символической записи

Выразим теперь остальные неизвестные параметры из системы уравнений (1.8.54):

Полученные выражения для коэффициентов a₀,a₁,a₂, подставим в уравнение сглаживающего квадратического полинома:

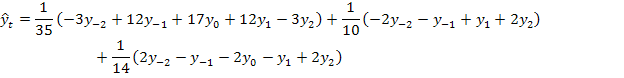
Последовательно подставляя в это выражение t=1;2, получим весовые коэффициенты для восстановления последних уровней ряда:

- при t=l (восстановление предпоследнего уровня ряда)

-при t=2( восстановление последнего уровня ряда)

Если последними пятью уровнями ряда были 0; 1; 4; 9; 16, то восстановление двух последних значений осуществлялось бы следующим образом:

• при t=1

-при t=2

Задача №4

Методы аналитического выравнивания и прогнозирования временных радов.

_{Необходимо выравнить рад динамики с помощью уравнения линейного тренда y=a0+a1}

t	yt	t2	yt
1	387,6	1	387,6	403,5
2	399,9	4	799,8	396,9
3	404,4	9	1212,0	390,2
4	383,1	16	1532,4	383,6
5	376,9	25	1884,5	376,9
6	377,7	36	2266,2	370,3
7	358,1	49	2506,7	363,7
8	371,9	64	2975,2	357,1
9	337,4	81	3000,6	350,4
Итого	3392,6	285	16565,0	3392,6

Решение:

Параметры a0 и a1 находим по формулам:

n=9

Подставляя в уравнение yt=410,12-6,63t вместо t числовые значения текущих лет (дней, месяцев) - 1,2,3,...n получим выравненные значения yt то есть t (графа 5 таблицы1).

Задача №5.

Методы аналитического выравнивания и прогнозирования временного ряда.

В таблице 1. представлен ряд динамики условного экономического показателя (у) за девять лет (t).

t	1	2	3	4	5	6	7	8	9
y	387,6	399,9	404,0	383,1	376,9	377,7	358,1	371,9	333,4

Рассчитать доверительный интервал прогноза по уровню тренда.

Решение:

По данным таблицы 1. построим уравнение линейного тренда.

y=a₀+a₁

Расчет параметров a₀,a₁ производится по методу наименьших квадратов, для чего строится система нормальных уравнений:

отсюда,

В результате получим линейное уравнение у = 410,12 — 6,63 t

,R² =0,716

Последовательно подставляя в полученное уравнение вместо t его численные значения 1-год, 2-год,3-год и т.д. получим расчетные значения _t.

t	yt	t	(yt- t)	(yt- t)2
1	387,6	403,5	-15,9	252,81
2	399,9	396,9	3,0	9,0
3	404,0	390,2		190,44
4	383,1	383,6	-0,5	0,25
5	376,9	_376,9	0	0
6	377.7	370,3	7,4	154,76
7	358,1	363,7	-5,6	31,36
8	371,9	537,1	14,8	219,04
9	333,4	350,4	-17,0	289,4
0 1046,66

Колеблемость уровней динамического ряда относительно тренда определяется по формуле

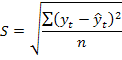
Тогда доверительный интервал для тренда составит:

_t±t_aS

где t_a- табличное значение критерия Стьюдента.

При a=0,05 и числе степеней свободы равном 7 ,для нашего примера, t_a = 2,365 и доверительный интервал для тренда равен

±10,78 • 2,365 или _t = ±25,5

Если распространить этот интервал прогноза на следующий 10-й год (t=10), то он составит =10 ±25,5или при ₌₁₀ =343,8 прогнозная величина находится в интервале

343,4-25,5≤y_t=10≤343,8+25,5

318,3≤y_t=10≤369,3

Задаче № 6.

Методы изучения сезонных колебаний.

В таблице 1 представлены условные данные о ежемесячном выпуске продукция за три года . Необходимо рассчитать индекс сезонности.

Таблица 1.

Производство условного продукта по месяцам в расчет индексов.

месяц	1-й год	2-й год	3-й год	В среднем за месяц i	Is%
1	10,2	9,7	11,8	10,6	57,6
2	15,2	16,1	14,4	15,2	82,5
3	17,3	14,8	15,6	15,9	86,3
4	19,4	22,7	16,5	19,5	105,9
5	21,2	25,4	29,1	25,2	136,8
6	26,1	28,2	25,2	26,5	143,9
7	28,3	25,8	23,5	25,6	140,6
8	21,4	23,3	23,6	22,8	123,8
9	22,1	20,7	18,2	20,3	110,2
10	14,6	15,2	16,3	15,4	83,6
11	9,5	8,6	13,3	10,5	157,0
12	12,4	12,9	14,6	13,3	72,2
Итого	217,7	223,4	221,1	221,1	1200,4
В среднем	18,14	18,61	18,51	=18,42	100

Решение:

Для каждого месяца рассчитывается средняя величина уровня. В нашем примере за три года ( ). Затем вычисляется среднемесячный уровень для всего ряда . После чего определяется показатель сезонной волны - индекс сезонности I_s как процентное отношение средних для каждого месяца к общему среднемесячному уровню, %.

где - средний уровень для каждого месяца (за три года); - среднемесячный уровень для всего ряда.

Средний индекс сезонности для 12 месяцев должен быть равен 100%, тогда сумма индексов должна составлять 1200. В нашем примере это отношение равно 1200,4 (небольшая погрешность — следствие округления).

Задача № 7.

Упрощенные приемы прогнозирования. Прибыть за год характеризуется данными , приведенными в таблице 1.

	, прибыль, тыс.руб.	2
1-е полугодие	63,5	0,92
2-е полугодие	64,5	0,86

Оценим существенность различий в дисперсиях: F=0,92/0,86=1,07 при табличном значении 5,05 (для а =0,05 и при числе степеней свободы 5 и 5). Дисперсии можно признать равными. Тогда оценим существенность расхождения в среднемесячных уровнях прибыли за каждое полугодие по t-критерию Стьюдента:

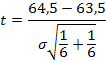
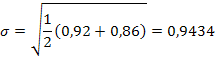
Произведя дальнейшие вычисления, находим, что t= 1,84 . Это меньше

i_т=2,23. Следовательно, с вероятностью 0,95 можно признать, что тенденции в ряду динамики нет.

Прогноз по стационарному ряду основан на предположении о неизменности в будущем среднего уровня динамического ряда, т.е.

y_p=

где y_p - прогнозное значение. Так как средний уровень

динамического ряда имеет погрешность как выборочная средняя и, кроме того, отдельные уровни ряда колеблются вокруг среднего значения, принято прогноз давать в интервале:

где — среднее значение по динамическому ряду:

-среднее квадратическое отклонение по динамическому ряду;

n- длина динамического ряда. - табличное значение t-критерия Стьюдента при уровне значимости а числе степеней свободы (n-1). Для нашего примера:

=1/2(63,5+64,5)=64,0

где - межгрупповая дисперсия; - внутригрупповая

дисперсия.

и

t_a=0,05,_n-1=11=2,201

Тогда ошибка прогноза составит:

2,201

Соответственно прогноз прибыли на январь следующего года окажется таким:

61

Задача № 8.

Метод экспоненциального сглаживания.

Рассчитайте экспоненциальную среднюю для временного ряда курса акций фирмы IBM (таблица 1).

В качестве начального значения экспоненциальной средней возьмите среднее значение из пяти первых уровней ряда. Расчеты проведите для двух различных значений параметров адаптации а:

а) а=0,1 ; б) а=0,5.

Курс акций фирмы IBM долл. США Таблица 1.

t	yt	t	yt	t	yt
1	510	11	494	21	523
2	497	12	499	22	527
3	504	13	502	23	523
4	510	14	509	24	528
5	509	15	525	25	529
6	503	16	512	26	538
7	500	17	510	27	539
8	500	18	506	28	541
9	500	19	515	29	543
10	495	20	522	30	541

Решение:

1. Определим

Найдем значения экспоненциальной средней при а=0,1

a=0,1 по условию

И т.д.

Результаты расчетов представлены в табл.2. Проведем аналогичные расчеты для а=0,5.

Результаты расчетов также представлены в таблице 2.

Экспоненциальные средние Таблица2.

t	а=0,1	а=0,5	t	а=0,1	а=0,5
1	506,4	508,0	16	505,7	513,3
2	505,5	502,5	17	506,1	511,7
3	505,3	503,2	18	506,1	5О8,8
4	505,8	506,6	19	507,0	511,9
5	506,1	507,8	20	508,5	517,0
6	505,8	505,4	21	509,9	520,0
7	505,2	502,7	22	511,6	523,5
8	504,7	501,4	23	512,8	523,2
9	504,2	500,7	24	514,3	525,6
10	503,3	497,8	25	515,8	527,3
11	502,4	495,9	26	518,0	523,7
12	502,0	497,5	27	520,1	525,8
13	502,0	499,7	28	522,2	538,4
14	502,7	504,4	29	524,3	540,7
15	505,0	514,7	30	525,9	540,9

При а=0,1 экспоненциальная средам носит более гладкий характер ,так как в этом случае в случае в наибольшей степени поглощаются случайные колебания временного ряда.

Задача №9.

Метод гармонических весов.

В таблице 1 дан ряд динамики производства продукции за 9 лет.

Таблица 1

1-год	2- год	3-год	4-год	5-год	6-год	7-год	8-год	9-год
10,0	11,1	12,1	12,5	13,7	13,9	19,6	15,9	19,0

Решение:

Предварительно ряд динамики был проверен на выполняемость предпосылок, на которых базируется метод. Далее находим параметры уравнений отдельных фаз движения скользящего тренда. В нашем примере к=3 , тогда находим : (9-3+1)=7 уравнений:

С помощью полученных уравнений определяем значение скользящего тренда.

При t=1 имеем одно значение которое получаем из

уравнения

При t=2 имеем два значения , которые получаем из уравнений:

Отсюда

Аналогично находим все значения:

12,68

Затем были рассчитаны приросты по формуле (7. 27 )

и гармонические веса по формуле (7.31)

Гармонические коэффициенты получим по формуле (7.32):

С₂ = 0,0156

С₃ = 0,0335

С₄ = 0,0543

С₅ = 0,0793

С₆ =0,1106

С₇= 0,1522

С₈= 0,2147

С₉ = 0,3397

Все эти коэффициенты удовлетворяют условиям 7.29, Используя формулу 7.28. находим средний абсолютный

прирост ( = 1,51) и рассчитаем прогнозные значения производства продукции по формуле 7.33.

y₁₀=20,51 y₁₁=22,02

y₁₂= 23,53