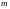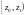- •№1. Случайные события. Классификация. Действия над событиями.
- •№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
- •№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
- •№4. Теорема сложения. Следствия.
- •Теорема доказана.
- •№7. Формула полной вероятности и формула Байеса. Примеры.
- •№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
- •№9. Случайная величина. Функция распределения случайной величины и её свойства.
- •№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
- •№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
- •№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
- •№16. Нормальный случайный вектор.
- •№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
- •№20. Ряд распределения функции дискретной случайной величины.
- •№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
- •24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
- •№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
- •№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
- •№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.
- •№30. Точечные оценки и их свойства.
- •№31. Функция правдоподобия. Неравенство Рао-Крамера. Критерий эффективности Рао-Крамера.
- •№37. Критерий согласия . Пример.
24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
Распределение
 .
.
Рассмотрим
гамма распределение (описывает времена
безотказной работы различных технических
устройств) с плотностью
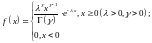 ,
где
,
где
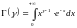 – гамма-функция Эйлера.
– гамма-функция Эйлера.
Если
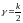 ,
где
– нечётное число, а
,
где
– нечётное число, а
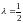 ,
то гамма-распределение превращается в
распределение
(хи-квадрат). Параметр
называют в этом случае числом степеней
свободы распределения
.
,
то гамма-распределение превращается в
распределение
(хи-квадрат). Параметр
называют в этом случае числом степеней
свободы распределения
.
Распределение Стьюдента (Госсета).
Распределением
Стьюдента (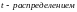 )
называют распределение с плотностью
)
называют распределение с плотностью
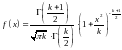 .
.
Распределение Фишера (Снедекора).
Пусть
независимые случайные величины
и
имеют распределение
с
и
степенями свободы соответственно.
Распределением Фишера (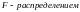 )
называется распределение случайной
величины
)
называется распределение случайной
величины
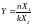 ,
плотность которого выражается следующей
формулой:
,
плотность которого выражается следующей
формулой:
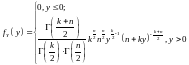 .
.
№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
Математическая статистика – раздел прикладной математики, посвящённый методам систематизации и анализа статистических данных с целью построения вероятностной модели случайных явлений, а также уточнения их параметров.
Сопоставляя задачи теории вероятностей и математической статистики, можно говорить о том, что задачи математической статистики являются теоретически обработанными выводами теории вероятностей. В задачах теории вероятностей, как правило, вероятностная модель дана, и необходимо по одним её параметрам получить другие. В задачах математической статистики неизвестна либо вся вероятностная модель, либо её параметры, и необходимо, основываясь на статистических данных, получить неизвестные части вероятностной модели или вынести определённые суждения о них.
Таким
образом исходными для задач математической
статистики являются статистические
данные, которые как правило имеют
численную природу. Статистические
данные получаются в результате
статистического эксперимента,
заключающегося в
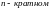 измерении значения некоторой случайной
величины. Результаты измерений
записываются последовательно.
измерении значения некоторой случайной
величины. Результаты измерений
записываются последовательно.
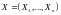 – выборка объёма
,
– элементы выборки.
– многомерная случайная величина, т.к.
результат
– выборка объёма
,
– элементы выборки.
– многомерная случайная величина, т.к.
результат
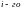 измерения заранее предсказать нельзя.
В результате конкретного измерения
получается реализация выборки
измерения заранее предсказать нельзя.
В результате конкретного измерения
получается реализация выборки
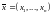 ,
где
– выборочные значения.
,
где
– выборочные значения.
Необходимым условием решения задач математической статистики является условие репрезентативности, т.е. выборка должна отражать закон распределения случайной величины.
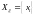 – генеральная совокупность (множество
всех возможных выборочных значений).
Выборка взята из генеральной совокупности
,
если она получена из измерения случайной
величины
.
– генеральная совокупность (множество
всех возможных выборочных значений).
Выборка взята из генеральной совокупности
,
если она получена из измерения случайной
величины
.
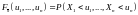 – закон распределения выборки. В случае
независимости измерений
– закон распределения выборки. В случае
независимости измерений
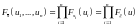 .
.
Если
выборка репрезентативна, то каждый её
элемент имеет то же распределение, что
и наблюдаемая случайная величина:
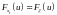 .
.
По умолчанию считаем измерения независимыми.
№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
Оценка вероятности события.
Пусть – случайное событие. Необходимо построить оценку вероятности .
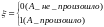 ,
тогда
,
тогда
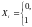 .
.
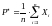 – оценка,
– оценка,
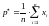 – значение оценки.
– значение оценки.
Оценка функции распределения.
Дана
выборка
из
.
Необходимо оценить
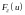 .
.
Сначала
функция распределения представляется
в виде
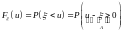 .
Т.о. задачу можно свести к оценке
вероятности события:
.
Т.о. задачу можно свести к оценке
вероятности события:
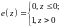 ,
тогда
,
тогда
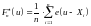 – оценка функции распределения,
– оценка функции распределения,
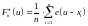 – эмпирическая функция распределения.
– эмпирическая функция распределения.
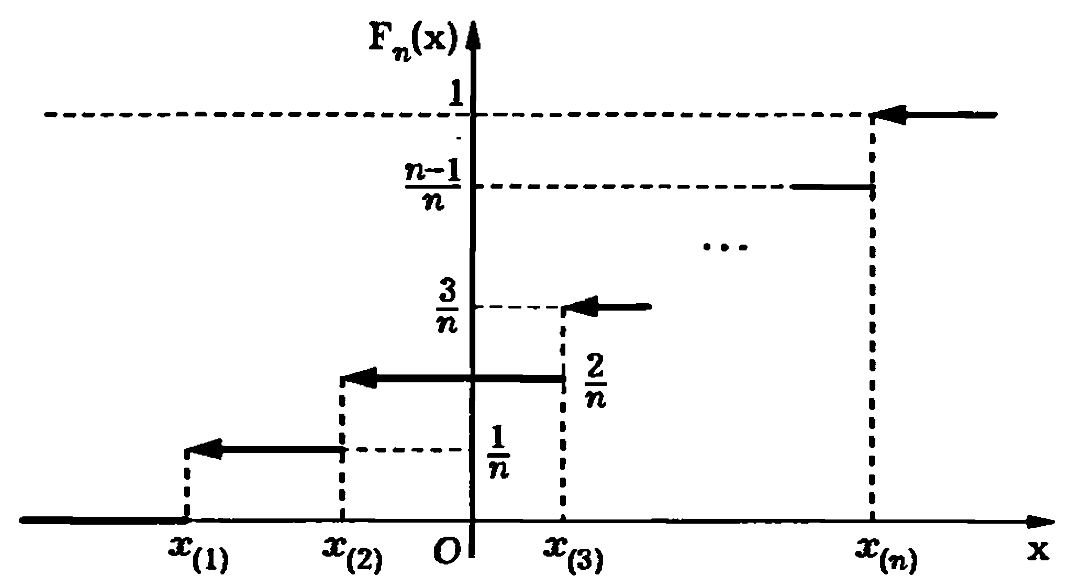 1.
Если все выборочные значения
различны, то функцию
1.
Если все выборочные значения
различны, то функцию
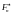 можно записать в следующем виде:
можно записать в следующем виде:
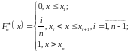 ,
т.е. в каждой точке
функция
,
т.е. в каждой точке
функция
 имеет скачок величиной
имеет скачок величиной
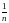 .
На рисунке изображён график функции
:
.
На рисунке изображён график функции
:
2.
Группированная выборка.
– непрерывная случайная величина,
– достаточно большое число. Разобьём
множество значений
на интервалы
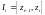 ,
получим группированную выборку:
,
получим группированную выборку:
Номер интервала |
|
|
|
|
Сам интервал |
|
|
|
|
Количество знач. |
|
|
|
|
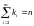 ;
;
 .
.
Оценка плотности вероятностей.
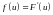 ,
,
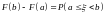 ,
а с другой стороны
,
а с другой стороны
 – формула конечных приращений Лагранжа.
– формула конечных приращений Лагранжа.
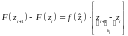 ,
,
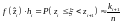 .
.
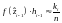 ,
где
,
где
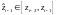 ,
,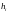 – длина
отрезка.
– длина
отрезка.
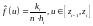 – оценка плотности распределения.
– оценка плотности распределения.
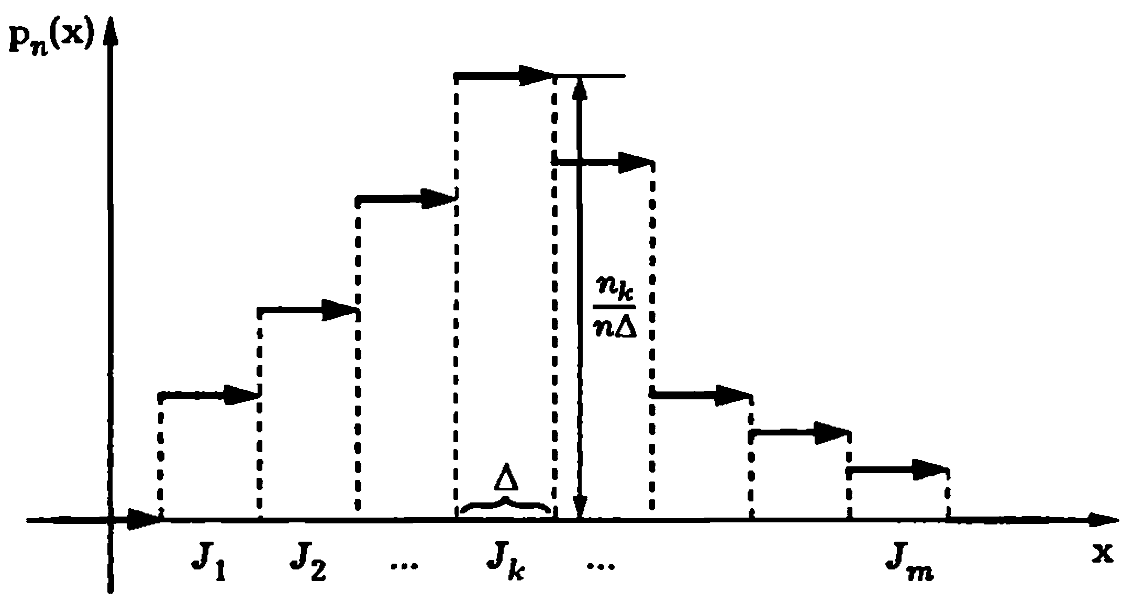 График
плотности распределения (гистограмма)
изображён на рисунке:
График
плотности распределения (гистограмма)
изображён на рисунке: