
- •№1. Случайные события. Классификация. Действия над событиями.
- •№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
- •№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
- •№4. Теорема сложения. Следствия.
- •Теорема доказана.
- •№7. Формула полной вероятности и формула Байеса. Примеры.
- •№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
- •№9. Случайная величина. Функция распределения случайной величины и её свойства.
- •№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
- •№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
- •№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
- •№16. Нормальный случайный вектор.
- •№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
- •№20. Ряд распределения функции дискретной случайной величины.
- •№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
- •24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
- •№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
- •№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
- •№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.
- •№30. Точечные оценки и их свойства.
- •№31. Функция правдоподобия. Неравенство Рао-Крамера. Критерий эффективности Рао-Крамера.
- •№37. Критерий согласия . Пример.
№20. Ряд распределения функции дискретной случайной величины.
Рассмотрим
на вероятностном пространстве
двумерный случайный вектор
и числовую функцию
 числовых аргументов
и
.
числовых аргументов
и
.
Случайную
величину
 называют функцией (скалярной) от двумерной
случайной величины (двумерного случайного
вектора)
называют функцией (скалярной) от двумерной
случайной величины (двумерного случайного
вектора)
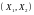 .
Функция
от двумерной дискретной случайной
величины является дискретной случайной
величиной, принимающей значения
.
Функция
от двумерной дискретной случайной
величины является дискретной случайной
величиной, принимающей значения
 с вероятностью
с вероятностью
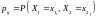 ,
где
,
где
 и
и
 – значения случайных величин
и
соответственно.
– значения случайных величин
и
соответственно.
Чтобы
построить ряд распределения дискретной
случайной величины
 ,
необходимо, во-первых, не учитывать все
те значения
,
вероятность принять которые случайной
величине
равна нулю, а во-вторых, объединить в
один столбец все одинаковые значения
случайной величины
,
приписав этому столбцу суммарную
вероятность.
,
необходимо, во-первых, не учитывать все
те значения
,
вероятность принять которые случайной
величине
равна нулю, а во-вторых, объединить в
один столбец все одинаковые значения
случайной величины
,
приписав этому столбцу суммарную
вероятность.

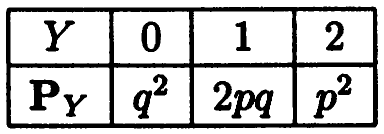 Пример:
Пусть
–
случайная величина, равная суммарному
числу успехов в двух испытаниях по схеме
Бернулли, а
– число успехов в
испытании,
Пример:
Пусть
–
случайная величина, равная суммарному
числу успехов в двух испытаниях по схеме
Бернулли, а
– число успехов в
испытании,
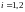 .
Тогда
.
Тогда
 и
и
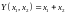 .
Заметим, что двум средним столбцам
соответствует одно и то же значение 1
случайной величины
,
и их следует объединить. Окончательно
получаем ряд распределения случайной
величины
,
представленный в следующей таблице:
.
Заметим, что двум средним столбцам
соответствует одно и то же значение 1
случайной величины
,
и их следует объединить. Окончательно
получаем ряд распределения случайной
величины
,
представленный в следующей таблице:
№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
Пусть
– двумерная непрерывная случайная
величина с плотностью распределения
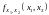 .
Функцию распределения случайной величины
можно найти по формуле:
.
Функцию распределения случайной величины
можно найти по формуле:
 (1), где область интегрирования состоит
из всех значений
и
,
для которых
(1), где область интегрирования состоит
из всех значений
и
,
для которых
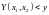 .
.
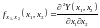 – плотность распределения функции
.
– плотность распределения функции
.
Пусть
,
где
и
– независимые случайные величины, тогда
по формуле (1) находим:
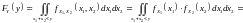
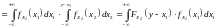 .
.
Дифференцируя
последнюю формулу по
под знаком интеграла, получаем (с учётом
переобозначения
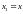 )
выражение для плотности
)
выражение для плотности
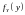 распределения суммы
и
:
распределения суммы
и
:
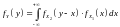 (2). В этом случае говорят, что плотность
распределения
случайной величины
является свёрткой (композицией) плотностей
распределения
(2). В этом случае говорят, что плотность
распределения
случайной величины
является свёрткой (композицией) плотностей
распределения
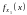 и
и
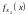 слагаемых
и
или что закон распределения суммы двух
независимых случайных величин является
свёрткой (композицией) законов
распределения слагаемых. Соотношение
(2) условно записывают в виде
слагаемых
и
или что закон распределения суммы двух
независимых случайных величин является
свёрткой (композицией) законов
распределения слагаемых. Соотношение
(2) условно записывают в виде
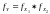 .
.
Формулу (2) называют формулой свёртки для плотностей распределения случайных величин и .
Пример: Пусть и – независимые случайные величины, распределённые по нормальному закону со средними значениями и и средними квадратичными отклонениями и . Найдём плотность распределения суммы .
Воспользовавшись
формулой свёртки, имеем: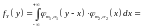
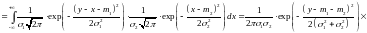
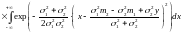 .
.
Делая
теперь замену
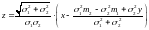 ,
получаем:
,
получаем:
 .
.
Таким
образом, случайная величина
также распределена по нормальному
закону с параметрами
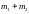 и
и
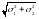 ,
т.е. композиция плотностей нормальных
законов распределения является плотностью
нормального закона распределения.
,
т.е. композиция плотностей нормальных
законов распределения является плотностью
нормального закона распределения.
№22. Характеристическая функция и её свойства.
Характеристической
функцией случайной величины
называется математическое ожидание
случайной величины
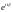 :
:
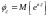 .
Если
есть функция распределения величины
,
то характеристическая функция равна:
.
Если
есть функция распределения величины
,
то характеристическая функция равна:
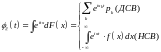 .
.
Свойства:
Характеристическая функция равномерно непрерывна на всей прямой и удовлетворяет следующим соотношениям:
 ;
;Если
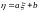 ,
где
,
где
 и
и
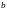 – постоянные, то
– постоянные, то
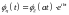 .
.Характеристическая функция суммы двух независимых случайных величин равна произведению их характеристических функций.
№23. Характеристическая функция и моменты случайной величины.
Характеристическая функция.
Характеристической функцией случайной величины называется математическое ожидание случайной величины : . Если есть функция распределения величины , то характеристическая функция равна: .
Моменты случайной величины.
Начальным
моментом порядка
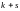 системы
называется величина
системы
называется величина
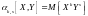 .
.
Центральным
моментом порядка
системы
называется величина
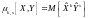 ,
где
,
где
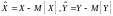 .
.
Расчётные формулы для определения моментов:
а) Для дискретных случайных величин.

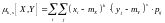
б) Для непрерывных случайных величин.
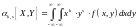 ,
,
 ,
где
,
где
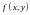 – плотность распределения системы.
– плотность распределения системы.
Корреляционным
моментом
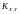 двух случайных величин
называется центральный момент порядка
двух случайных величин
называется центральный момент порядка
 ,
т.е.
,
т.е.
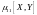 (второй смешанный центральный момент):
(второй смешанный центральный момент):
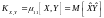 .
.
