
- •№1. Случайные события. Классификация. Действия над событиями.
- •№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
- •№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
- •№4. Теорема сложения. Следствия.
- •Теорема доказана.
- •№7. Формула полной вероятности и формула Байеса. Примеры.
- •№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
- •№9. Случайная величина. Функция распределения случайной величины и её свойства.
- •№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
- •№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
- •№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
- •№16. Нормальный случайный вектор.
- •№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
- •№20. Ряд распределения функции дискретной случайной величины.
- •№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
- •24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
- •№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
- •№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
- •№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.
- •№30. Точечные оценки и их свойства.
- •№31. Функция правдоподобия. Неравенство Рао-Крамера. Критерий эффективности Рао-Крамера.
- •№37. Критерий согласия . Пример.
№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
Классическое определение вероятности.
Пусть
всего
 элементарных исходов,
элементарных исходов,
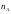 – число исходов, благоприятствующих
событию
.
Тогда
– число исходов, благоприятствующих
событию
.
Тогда
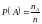 – вероятность.
– вероятность.
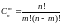 – число
сочетаний. Если опыт состоит в выборе
– число
сочетаний. Если опыт состоит в выборе
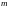 элементов из
без упорядочения и без возвращения, то
общее число элементарных исходов в
опыте будет равно количеству различных
элементов из
без упорядочения и без возвращения, то
общее число элементарных исходов в
опыте будет равно количеству различных
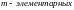 комбинаций, отличных друг от друга, по
крайней мере, одним составом элементов.
комбинаций, отличных друг от друга, по
крайней мере, одним составом элементов.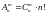 – число
размещений без повторений. Если опыт
состоит в выборе
элементов из
без возвращения, но с упорядочением
элементов по мере их поступления, то
количество элементарных исходов равно
числу
комбинаций, отличных друг от друга либо
порядком следования элементов, либо
их составом (но один и тот же элемент
встречается в группе не более одного
раза).
– число
размещений без повторений. Если опыт
состоит в выборе
элементов из
без возвращения, но с упорядочением
элементов по мере их поступления, то
количество элементарных исходов равно
числу
комбинаций, отличных друг от друга либо
порядком следования элементов, либо
их составом (но один и тот же элемент
встречается в группе не более одного
раза).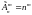 – число
размещений с повторениями. Если опыт
состоит в выборе
элементов из
с возвращением и упорядочением элементов
по мере их поступления, то общее число
исходов опыта равно количеству
комбинаций, отличающихся друг от друга
составом элементов, либо порядком их
следования (при этом один и тот же
элемент может повторяться несколько
раз).
– число
размещений с повторениями. Если опыт
состоит в выборе
элементов из
с возвращением и упорядочением элементов
по мере их поступления, то общее число
исходов опыта равно количеству
комбинаций, отличающихся друг от друга
составом элементов, либо порядком их
следования (при этом один и тот же
элемент может повторяться несколько
раз).
Геометрическое определение вероятности.
Если
множество элементарных исходов может
быть представлено некоторой областью
 ,
а множество благоприятствующих событию
исходов – подобластью
,
а множество благоприятствующих событию
исходов – подобластью
 ,
то
,
то
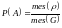 .
.
Статистическое определение вероятности.
Рассмотрим
опыт, в котором событие
может появиться, а может и не появиться,
и проведём этот опыт
раз. Пусть
раз событие
произошло, тогда
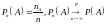 .
.
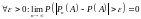 – сходимость
по вероятности.
– сходимость
по вероятности.
Вероятностью
события
называют (эмпирический) предел
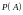 ,
к которому стремится частота
,
к которому стремится частота
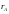 события
при неограниченном увеличении числа
события
при неограниченном увеличении числа
 опытов.
опытов.
№4. Теорема сложения. Следствия.
Теорема:
.
Для
событий:
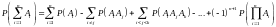 .
.
 Доказательство:
пусть всего
исходов.
Доказательство:
пусть всего
исходов.
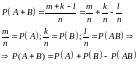
Теорема доказана.
Следствие
1:
если
и
несовместны, то
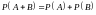 .
.
Следствие 2:
Доказательство:
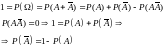
№5. Условная вероятность и её свойства. Теорема умножения вероятностей.
Говорят, что событие зависит от события , если его вероятность меняется, когда происходит событие .
Условная
вероятность – это вероятность события
,
подсчитанная при условии, что
произошло. ( –
–
 от
при условии
)
от
при условии
)
Если
события
и
независимы, то
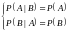 .
.
Теорема:
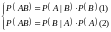 Для
событий:
Для
событий:
 .
.
Доказательство:
пусть всего
исходов.
благоприятствуют
исходов,
благоприятствуют
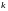 исходов,
исходов,
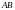 –
–
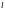 исходов. Пусть
произошло, осталось
исходов,
из них благоприятствуют
.
исходов. Пусть
произошло, осталось
исходов,
из них благоприятствуют
.
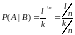
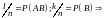
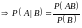 .
Теорема
доказана.
.
Теорема
доказана.
Следствие
1:
если
не зависит от
,
то
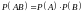 .
.
Следствие 2: если зависит от , то зависит от .
№6. Независимость событий и независимость испытаний.
События и называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий
.
Свойство независимости событий взаимно, то есть если зависит от , то зависит от .
События
и
,
имеющие ненулевую вероятность, являются
независимыми тогда и только тогда, когда
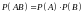 .
.
События
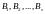 называются независимыми в совокупности,
если для любого события
называются независимыми в совокупности,
если для любого события
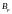 из их числа и произвольных
из их числа и произвольных
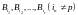 из их же числа события
из их же числа события
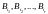 взаимно независимы. В силу теоремы
умножения, это определение эквивалентно
следующему: при любых
взаимно независимы. В силу теоремы
умножения, это определение эквивалентно
следующему: при любых
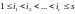 и
и

 .
Заметим, что для независимости в
совокупности нескольких событий
недостаточно их попарной независимости.
.
Заметим, что для независимости в
совокупности нескольких событий
недостаточно их попарной независимости.
Рассмотрим опыт, состоящий в проведении двух испытаний. Эти испытания называются независимыми, если любые два события и , из которых определяется по исходу первого испытания, а – по исходу второго, являются независимыми.
