
- •№1. Случайные события. Классификация. Действия над событиями.
- •№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
- •№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
- •№4. Теорема сложения. Следствия.
- •Теорема доказана.
- •№7. Формула полной вероятности и формула Байеса. Примеры.
- •№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
- •№9. Случайная величина. Функция распределения случайной величины и её свойства.
- •№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
- •№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
- •№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
- •№16. Нормальный случайный вектор.
- •№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
- •№20. Ряд распределения функции дискретной случайной величины.
- •№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
- •24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
- •№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
- •№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
- •№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.
- •№30. Точечные оценки и их свойства.
- •№31. Функция правдоподобия. Неравенство Рао-Крамера. Критерий эффективности Рао-Крамера.
- •№37. Критерий согласия . Пример.
№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
Математическое ожидание случайной величины.
 –
математическое
ожидание (среднее значение случайной
величины).
–
математическое
ожидание (среднее значение случайной
величины).
Свойства математического ожидания:
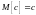 ,
где
,
где
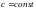 ;
;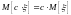 ;
;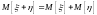 ;
;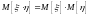 ,
если
и
,
если
и
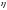 независимы.
независимы.
Функции случайной величины.
Пусть
на вероятностном пространстве
 ,
где
–
,
где
–
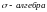 ,
задана случайная величина
,
задана случайная величина
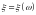 .
Рассмотрим действительную функцию
.
Рассмотрим действительную функцию
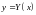 действительного аргумента
действительного аргумента
 (область определения которой включает
в себя множество возможных значений
случайной величины
).
(область определения которой включает
в себя множество возможных значений
случайной величины
).
Случайную
величину
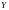 ,
которая каждому элементарному исходу
ставит в соответствие число
,
которая каждому элементарному исходу
ставит в соответствие число
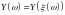 ,
называют функцией
,
называют функцией
 от скалярной случайной величины
.
от скалярной случайной величины
.
№13. Дисперсия и её свойства. Моменты случайной величины.
Дисперсия и её свойства.
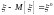 – центрированная случайная величина
(отклонение
от
– центрированная случайная величина
(отклонение
от
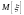 ),
),
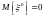 .
.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения от .
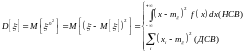
Свойства дисперсии:
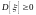 ;
;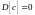 ,
где
;
,
где
;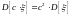 ;
;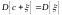 ;
;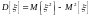
Доказательство:

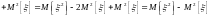 ,
ч.т.д.
,
ч.т.д.
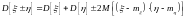 – ковариация
(
– ковариация
(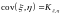 ,
,
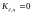 ,
когда
,
когда
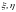 независимы).
независимы).
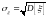 – среднее
квадратичное (квадратическое отклонение)
случайной величины
.
– среднее
квадратичное (квадратическое отклонение)
случайной величины
.
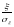 – нормированная случайная величина.
– нормированная случайная величина.

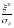 – стандартная случайная величина
– стандартная случайная величина
 .
.
Моменты случайной величины.
Моментом
 порядка случайной величины
называется математическое ожидание
величины
порядка случайной величины
называется математическое ожидание
величины
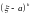 :
:
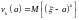 .
.
Если
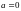 ,
то момент называется начальным. Легко
видеть, что начальный момент первого
порядка есть математическое ожидание
величины
.
,
то момент называется начальным. Легко
видеть, что начальный момент первого
порядка есть математическое ожидание
величины
.
Если
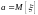 ,
то момент называется центральным. Легко
видеть, что центральный момент первого
порядка равен нулю, а центральный момент
второго порядка есть не что иное, как
дисперсия.
,
то момент называется центральным. Легко
видеть, что центральный момент первого
порядка равен нулю, а центральный момент
второго порядка есть не что иное, как
дисперсия.
Начальные
моменты будем обозначать буквой
 ,
а центральные – буквой
,
а центральные – буквой
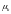 ,
указывая в обоих случаях нижним индексом
порядок момента.
,
указывая в обоих случаях нижним индексом
порядок момента.
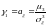 – коэффициент асимметрии.
– коэффициент асимметрии.
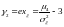 – коэффициент эксцесса.
– коэффициент эксцесса.
Мода
для дискретного распределения – точка
с максимальной вероятностью, а для
непрерывного – точка максимума
распределения (плотность в ней достигает
максимального значения):
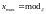 .
.
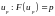 – квантиль распределения порядка
.
– квантиль распределения порядка
.
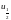 – медиана распределения.
– медиана распределения.
Для
НСВ квантиль определяется однозначно.
Для ДСВ понятие квантили не рассматривается.
Вероятность попадания величины слева
и справа от медианы одинакова:
 .
.
№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
Нормальный закон (для НСВ).
Случайная
величина распределена по нормальному
(или гауссову) закону, или имеет нормальное
(гауссово) распределение, если её
плотность
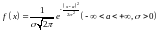 .
Нормальное распределение зависит от
двух параметров:
и среднего квадратического отклонения
.
Нормальное распределение зависит от
двух параметров:
и среднего квадратического отклонения
 ,
,
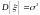 .
.
Равномерный закон (для НСВ).
Случайная
величина имеет равномерное распределение
на отрезке
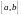 ,
если её плотность распределения
,
если её плотность распределения
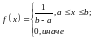 .
В данном случае
.
В данном случае
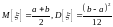 .
.
Биномиальный закон (для ДСВ).
Дискретная
случайная величина
распределена по биномиальному закону,
если она принимает значения
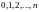 в соответствии с распределением, заданным
формулой
в соответствии с распределением, заданным
формулой
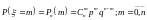 .
Здесь
.
Здесь
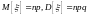 .
.
Показательный закон (для НСВ).
Случайная
величина распределена по показательному
(экспоненциальному) закону, если она
имеет плотность распределения
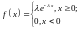 ,
где
,
где
 – параметр экспоненциального
распределения;
– параметр экспоненциального
распределения;
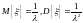 .
.
Закон Пуассона (для ДСВ).
ДСВ
распределена по закону Пуассона, если
она принимает целые неотрицательные
значения с вероятностями
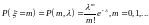 ;
;
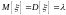 .
.
