№7. Формула полной вероятности и формула Байеса. Примеры.

_{Формула полной вероятности.}

_{Рассмотрим группу несовместных событий 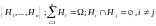. Эти события назовём гипотезами. Событие может произойти или нет в том же опыте, что и 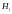. Т.к. 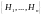– полная группа, то произойдёт с одной и только одной из гипотез вместе.}

_{Теорема: Пусть для некоторого события и гипотез 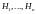известны 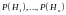и . Тогда безусловную вероятность определяют по формуле: 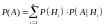– формула полной вероятности (ФПВ).}

_{Доказательство: 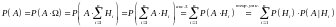. Теорема доказана.}

_{Пример: Студент Иванов выучил все экзаменационных билетов, но из них на «пять» – лишь 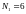. Определим, зависит или нет вероятность извлечения «счастливого» билета (событие ) от того, первым или вторым выбирает Иванов свой билет.}

_{Рассмотрим две ситуации.}

_{Иванов выбирает билет первым. Тогда .}

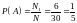_{Иванов выбирает билет вторым. Введём гипотезы: 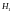– первый извлечённый билет оказался «счастливым», 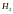– «несчастливым». Ясно, что 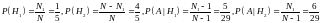. В силу формулы полной вероятности 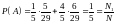, что совпадает с первой ситуацией.}

_{Формула Байеса.}

_{Пусть событие произошло, тогда имеет место следующая теорема.}

_{Теорема: Пусть для некоторого события и гипотез известны и . Тогда условная вероятность 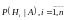, гипотезы при условии события определяется формулой Байеса .}

_{Доказательство: 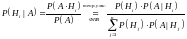. Теорема доказана.}

_{Заметим, что вероятности обычно называют априорными (т.е. полученными «до опыта»), а условные вероятности 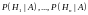– апостериорными (т.е. полученными «после опыта»).}

Пример: врач после осмотра больного считает, что возможно одно из двух заболеваний, которые мы зашифруем номерами 1 и 2, причём степень своей уверенности в отношении правильности диагноза он оценивает как 40% и 60% соответственно. Для уточнения диагноза больного направляют на анализ, исход которого даёт положительную реакцию при заболевании 1 в 90% случаев и при заболевании 2 _{– в 20% случаев. Анализ дал положительную реакцию. Как изменится мнение врача после этого?}

_{Обозначим через событие, означающее, что анализ дал положительную реакцию. Естественно ввести следующие гипотезы: – имеет место заболевание 1; – имеет место заболевание 2. Из условий задачи ясно, что априорные вероятности гипотез равны: 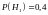и 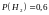, а условные вероятности события при наличии гипотез и равны 0,9 и 0,2 соответственно. Использую формулу Байеса, находим .}

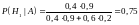_{Итак, врач с большей уверенностью признает наличие заболевания 1.}

№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.

_{Схема независимых испытаний Бернулли.}

_{Рассматривается независимых испытаний, в каждом из которых событие может произойти с вероятностью 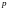и не произойти с вероятностью ( ).}

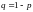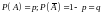_{Теорема: Вероятность 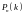того, что в испытаниях по схеме Бернулли произойдёт ровно 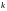успехов, определяется формулой Бернулли .}

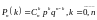_{Доказательство: Результат каждого опыта можно записать в виде последовательности УНН…У, состоящей из букв «У» и «Н», причём буква «У» на 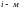месте означает, что в испытании произошёл успех, а «Н» – неудача. Пространство элементарных исходов состоит из 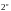исходов, каждый из которых отождествляется с определённой последовательностью УНН…У.}

_{Каждому элементарному исходу 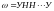можно поставить в соответствие вероятность .}

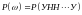_{В силу независимости испытаний события У, Н, Н,…, У являются независимыми в совокупности, и потому по теореме умножения вероятностей имеем 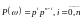, если в испытаниях успех «У» имел место 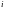раз, а неуспех «Н», следовательно, 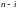раз.}

_{Событие 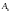происходит всякий раз, когда реализуется элементарный исход , в котором 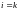. Вероятность любого такого элементарного исхода равна .}

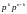_{Число таких исходов совпадает с числом способов, которыми можно расставить букв «У» на местах, не учитывая порядок, в котором их расставляют. Число таких способов равно .}

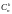_{Так как есть объединение (сумма) всех указанных элементарных исходов, то окончательно получаем для вероятности 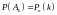формулу Бернулли. Теорема доказана.}

_{Из формулы Бернулли вытекают два следствия.}

1. _{Вероятность появления успеха (события ) в испытаниях не более 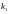и не менее 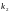раз равна .}

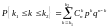2. _{В частном случае пр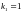и и 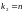из предыдущей формулы получаем формулу для вычисления вероятности хотя бы одного успеха в испытаниях: .}

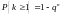_{Теорема Пуассона.}

_{Теорема: 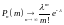, где .}

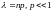_{Доказательство:}

_{. Теорема доказана.}

_{Предельная теорема Муавра-Лапласа.}

_{Теорема: .}
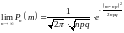